Adaptive Batch Size Schedules for Distributed Training of Language Models with Data and Model Parallelism

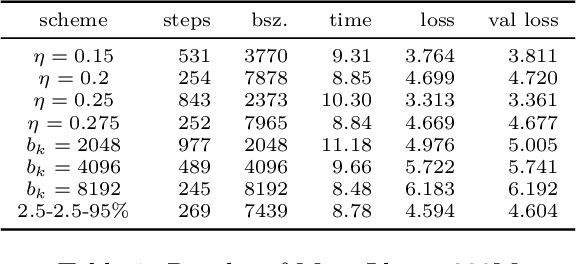
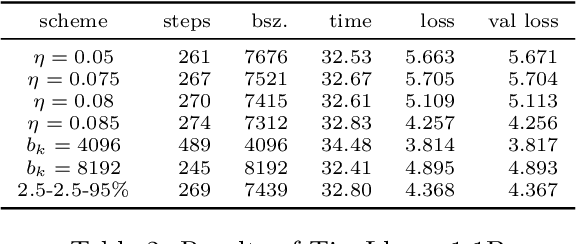
An appropriate choice of batch sizes in large-scale model training is crucial, yet it involves an intrinsic yet inevitable dilemma: large-batch training improves training efficiency in terms of memory utilization, while generalization performance often deteriorates due to small amounts of gradient noise. Despite this dilemma, the common practice of choosing batch sizes in language model training often prioritizes training efficiency -- employing either constant large sizes with data parallelism or implementing batch size warmup schedules. However, such batch size schedule designs remain heuristic and often fail to adapt to training dynamics, presenting the challenge of designing adaptive batch size schedules. Given the abundance of available datasets and the data-hungry nature of language models, data parallelism has become an indispensable distributed training paradigm, enabling the use of larger batch sizes for gradient computation. However, vanilla data parallelism requires replicas of model parameters, gradients, and optimizer states at each worker, which prohibits training larger models with billions of parameters. To optimize memory usage, more advanced parallelism strategies must be employed. In this work, we propose general-purpose and theoretically principled adaptive batch size schedules compatible with data parallelism and model parallelism. We develop a practical implementation with PyTorch Fully Sharded Data Parallel, facilitating the pretraining of language models of different sizes. We empirically demonstrate that our proposed approaches outperform constant batch sizes and heuristic batch size warmup schedules in the pretraining of models in the Llama family, with particular focus on smaller models with up to 3 billion parameters. We also establish theoretical convergence guarantees for such adaptive batch size schedules with Adam for general smooth nonconvex objectives.

High-Dimensional Markov-switching Ordinary Differential Processes

We investigate the parameter recovery of Markov-switching ordinary differential processes from discrete observations, where the differential equations are nonlinear additive models. This framework has been widely applied in biological systems, control systems, and other domains; however, limited research has been conducted on reconstructing the generating processes from observations. In contrast, many physical systems, such as human brains, cannot be directly experimented upon and rely on observations to infer the underlying systems. To address this gap, this manuscript presents a comprehensive study of the model, encompassing algorithm design, optimization guarantees, and quantification of statistical errors. Specifically, we develop a two-stage algorithm that first recovers the continuous sample path from discrete samples and then estimates the parameters of the processes. We provide novel theoretical insights into the statistical error and linear convergence guarantee when the processes are $\beta$-mixing. Our analysis is based on the truncation of the latent posterior processes and demonstrates that the truncated processes approximate the true processes under mixing conditions. We apply this model to investigate the differences in resting-state brain networks between the ADHD group and normal controls, revealing differences in the transition rate matrices of the two groups.

Trans-Glasso: A Transfer Learning Approach to Precision Matrix Estimation

Precision matrix estimation is essential in various fields, yet it is challenging when samples for the target study are limited. Transfer learning can enhance estimation accuracy by leveraging data from related source studies. We propose Trans-Glasso, a two-step transfer learning method for precision matrix estimation. First, we obtain initial estimators using a multi-task learning objective that captures shared and unique features across studies. Then, we refine these estimators through differential network estimation to adjust for structural differences between the target and source precision matrices. Under the assumption that most entries of the target precision matrix are shared with source matrices, we derive non-asymptotic error bounds and show that Trans-Glasso achieves minimax optimality under certain conditions. Extensive simulations demonstrate Trans Glasso's superior performance compared to baseline methods, particularly in small-sample settings. We further validate Trans-Glasso in applications to gene networks across brain tissues and protein networks for various cancer subtypes, showcasing its effectiveness in biological contexts. Additionally, we derive the minimax optimal rate for differential network estimation, representing the first such guarantee in this area.

High-Dimensional Differential Parameter Inference in Exponential Family using Time Score Matching

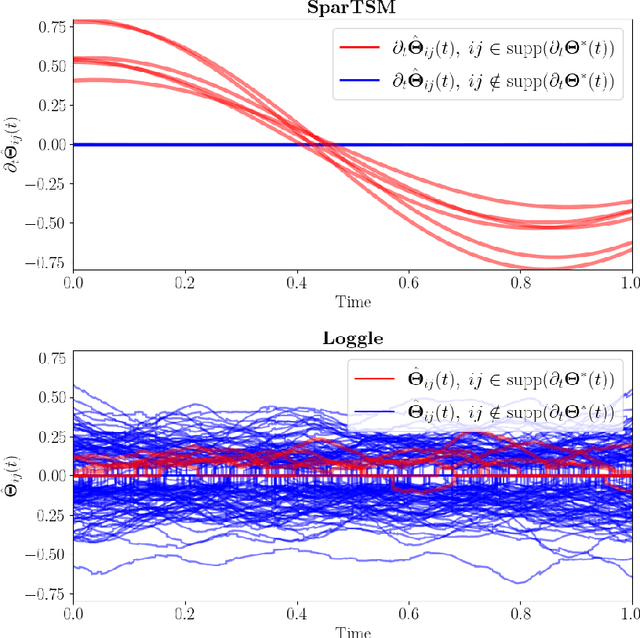
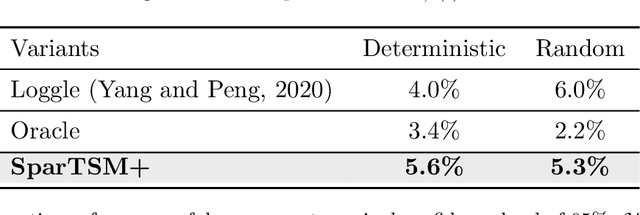
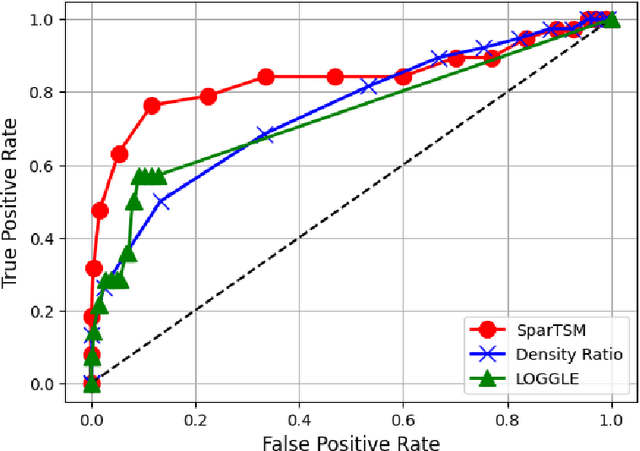
This paper addresses differential inference in time-varying parametric probabilistic models, like graphical models with changing structures. Instead of estimating a high-dimensional model at each time and inferring changes later, we directly learn the differential parameter, i.e., the time derivative of the parameter. The main idea is treating the time score function of an exponential family model as a linear model of the differential parameter for direct estimation. We use time score matching to estimate parameter derivatives. We prove the consistency of a regularized score matching objective and demonstrate the finite-sample normality of a debiased estimator in high-dimensional settings. Our methodology effectively infers differential structures in high-dimensional graphical models, verified on simulated and real-world datasets.

Pessimism Meets Risk: Risk-Sensitive Offline Reinforcement Learning

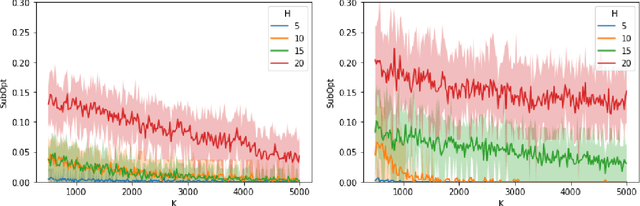
We study risk-sensitive reinforcement learning (RL), a crucial field due to its ability to enhance decision-making in scenarios where it is essential to manage uncertainty and minimize potential adverse outcomes. Particularly, our work focuses on applying the entropic risk measure to RL problems. While existing literature primarily investigates the online setting, there remains a large gap in understanding how to efficiently derive a near-optimal policy based on this risk measure using only a pre-collected dataset. We center on the linear Markov Decision Process (MDP) setting, a well-regarded theoretical framework that has yet to be examined from a risk-sensitive standpoint. In response, we introduce two provably sample-efficient algorithms. We begin by presenting a risk-sensitive pessimistic value iteration algorithm, offering a tight analysis by leveraging the structure of the risk-sensitive performance measure. To further improve the obtained bounds, we propose another pessimistic algorithm that utilizes variance information and reference-advantage decomposition, effectively improving both the dependence on the space dimension $d$ and the risk-sensitivity factor. To the best of our knowledge, we obtain the first provably efficient risk-sensitive offline RL algorithms.

Communication-Efficient Adaptive Batch Size Strategies for Distributed Local Gradient Methods

Modern deep neural networks often require distributed training with many workers due to their large size. As worker numbers increase, communication overheads become the main bottleneck in data-parallel minibatch stochastic gradient methods with per-iteration gradient synchronization. Local gradient methods like Local SGD reduce communication by only syncing after several local steps. Despite understanding their convergence in i.i.d. and heterogeneous settings and knowing the importance of batch sizes for efficiency and generalization, optimal local batch sizes are difficult to determine. We introduce adaptive batch size strategies for local gradient methods that increase batch sizes adaptively to reduce minibatch gradient variance. We provide convergence guarantees under homogeneous data conditions and support our claims with image classification experiments, demonstrating the effectiveness of our strategies in training and generalization.

Personalized Binomial DAGs Learning with Network Structured Covariates

The causal dependence in data is often characterized by Directed Acyclic Graphical (DAG) models, widely used in many areas. Causal discovery aims to recover the DAG structure using observational data. This paper focuses on causal discovery with multi-variate count data. We are motivated by real-world web visit data, recording individual user visits to multiple websites. Building a causal diagram can help understand user behavior in transitioning between websites, inspiring operational strategy. A challenge in modeling is user heterogeneity, as users with different backgrounds exhibit varied behaviors. Additionally, social network connections can result in similar behaviors among friends. We introduce personalized Binomial DAG models to address heterogeneity and network dependency between observations, which are common in real-world applications. To learn the proposed DAG model, we develop an algorithm that embeds the network structure into a dimension-reduced covariate, learns each node's neighborhood to reduce the DAG search space, and explores the variance-mean relation to determine the ordering. Simulations show our algorithm outperforms state-of-the-art competitors in heterogeneous data. We demonstrate its practical usefulness on a real-world web visit dataset.

AdAdaGrad: Adaptive Batch Size Schemes for Adaptive Gradient Methods

The choice of batch sizes in stochastic gradient optimizers is critical for model training. However, the practice of varying batch sizes throughout the training process is less explored compared to other hyperparameters. We investigate adaptive batch size strategies derived from adaptive sampling methods, traditionally applied only in stochastic gradient descent. Given the significant interplay between learning rates and batch sizes, and considering the prevalence of adaptive gradient methods in deep learning, we emphasize the need for adaptive batch size strategies in these contexts. We introduce AdAdaGrad and its scalar variant AdAdaGradNorm, which incrementally increase batch sizes during training, while model updates are performed using AdaGrad and AdaGradNorm. We prove that AdaGradNorm converges with high probability at a rate of $\mathscr{O}(1/K)$ for finding a first-order stationary point of smooth nonconvex functions within $K$ iterations. AdaGrad also demonstrates similar convergence properties when integrated with a novel coordinate-wise variant of our adaptive batch size strategies. Our theoretical claims are supported by numerical experiments on various image classification tasks, highlighting the enhanced adaptability of progressive batching protocols in deep learning and the potential of such adaptive batch size strategies with adaptive gradient optimizers in large-scale model training.

Inconsistency of cross-validation for structure learning in Gaussian graphical models

Despite numerous years of research into the merits and trade-offs of various model selection criteria, obtaining robust results that elucidate the behavior of cross-validation remains a challenging endeavor. In this paper, we highlight the inherent limitations of cross-validation when employed to discern the structure of a Gaussian graphical model. We provide finite-sample bounds on the probability that the Lasso estimator for the neighborhood of a node within a Gaussian graphical model, optimized using a prediction oracle, misidentifies the neighborhood. Our results pertain to both undirected and directed acyclic graphs, encompassing general, sparse covariance structures. To support our theoretical findings, we conduct an empirical investigation of this inconsistency by contrasting our outcomes with other commonly used information criteria through an extensive simulation study. Given that many algorithms designed to learn the structure of graphical models require hyperparameter selection, the precise calibration of this hyperparameter is paramount for accurately estimating the inherent structure. Consequently, our observations shed light on this widely recognized practical challenge.

Addressing Budget Allocation and Revenue Allocation in Data Market Environments Using an Adaptive Sampling Algorithm

High-quality machine learning models are dependent on access to high-quality training data. When the data are not already available, it is tedious and costly to obtain them. Data markets help with identifying valuable training data: model consumers pay to train a model, the market uses that budget to identify data and train the model (the budget allocation problem), and finally the market compensates data providers according to their data contribution (revenue allocation problem). For example, a bank could pay the data market to access data from other financial institutions to train a fraud detection model. Compensating data contributors requires understanding data's contribution to the model; recent efforts to solve this revenue allocation problem based on the Shapley value are inefficient to lead to practical data markets. In this paper, we introduce a new algorithm to solve budget allocation and revenue allocation problems simultaneously in linear time. The new algorithm employs an adaptive sampling process that selects data from those providers who are contributing the most to the model. Better data means that the algorithm accesses those providers more often, and more frequent accesses corresponds to higher compensation. Furthermore, the algorithm can be deployed in both centralized and federated scenarios, boosting its applicability. We provide theoretical guarantees for the algorithm that show the budget is used efficiently and the properties of revenue allocation are similar to Shapley's. Finally, we conduct an empirical evaluation to show the performance of the algorithm in practical scenarios and when compared to other baselines. Overall, we believe that the new algorithm paves the way for the implementation of practical data markets.