Traversing Pareto Optimal Policies: Provably Efficient Multi-Objective Reinforcement Learning

This paper investigates multi-objective reinforcement learning (MORL), which focuses on learning Pareto optimal policies in the presence of multiple reward functions. Despite MORL's significant empirical success, there is still a lack of satisfactory understanding of various MORL optimization targets and efficient learning algorithms. Our work offers a systematic analysis of several optimization targets to assess their abilities to find all Pareto optimal policies and controllability over learned policies by the preferences for different objectives. We then identify Tchebycheff scalarization as a favorable scalarization method for MORL. Considering the non-smoothness of Tchebycheff scalarization, we reformulate its minimization problem into a new min-max-max optimization problem. Then, for the stochastic policy class, we propose efficient algorithms using this reformulation to learn Pareto optimal policies. We first propose an online UCB-based algorithm to achieve an $\varepsilon$ learning error with an $\tilde{\mathcal{O}}(\varepsilon^{-2})$ sample complexity for a single given preference. To further reduce the cost of environment exploration under different preferences, we propose a preference-free framework that first explores the environment without pre-defined preferences and then generates solutions for any number of preferences. We prove that it only requires an $\tilde{\mathcal{O}}(\varepsilon^{-2})$ exploration complexity in the exploration phase and demands no additional exploration afterward. Lastly, we analyze the smooth Tchebycheff scalarization, an extension of Tchebycheff scalarization, which is proved to be more advantageous in distinguishing the Pareto optimal policies from other weakly Pareto optimal policies based on entry values of preference vectors. Furthermore, we extend our algorithms and theoretical analysis to accommodate this optimization target.

Pessimism Meets Risk: Risk-Sensitive Offline Reinforcement Learning

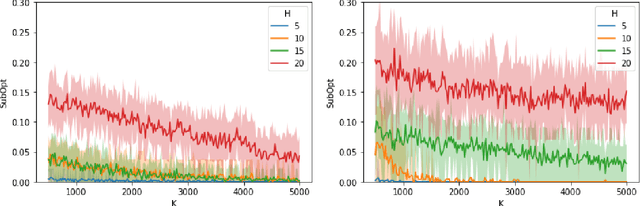
We study risk-sensitive reinforcement learning (RL), a crucial field due to its ability to enhance decision-making in scenarios where it is essential to manage uncertainty and minimize potential adverse outcomes. Particularly, our work focuses on applying the entropic risk measure to RL problems. While existing literature primarily investigates the online setting, there remains a large gap in understanding how to efficiently derive a near-optimal policy based on this risk measure using only a pre-collected dataset. We center on the linear Markov Decision Process (MDP) setting, a well-regarded theoretical framework that has yet to be examined from a risk-sensitive standpoint. In response, we introduce two provably sample-efficient algorithms. We begin by presenting a risk-sensitive pessimistic value iteration algorithm, offering a tight analysis by leveraging the structure of the risk-sensitive performance measure. To further improve the obtained bounds, we propose another pessimistic algorithm that utilizes variance information and reference-advantage decomposition, effectively improving both the dependence on the space dimension $d$ and the risk-sensitivity factor. To the best of our knowledge, we obtain the first provably efficient risk-sensitive offline RL algorithms.

ReadProbe: A Demo of Retrieval-Enhanced Large Language Models to Support Lateral Reading

With the rapid growth and spread of online misinformation, people need tools to help them evaluate the credibility and accuracy of online information. Lateral reading, a strategy that involves cross-referencing information with multiple sources, may be an effective approach to achieving this goal. In this paper, we present ReadProbe, a tool to support lateral reading, powered by generative large language models from OpenAI and the Bing search engine. Our tool is able to generate useful questions for lateral reading, scour the web for relevant documents, and generate well-attributed answers to help people better evaluate online information. We made a web-based application to demonstrate how ReadProbe can help reduce the risk of being misled by false information. The code is available at https://github.com/DakeZhang1998/ReadProbe. An earlier version of our tool won the first prize in a national AI misinformation hackathon.

A Joint Probabilistic Classification Model of Relevant and Irrelevant Sentences in Mathematical Word Problems

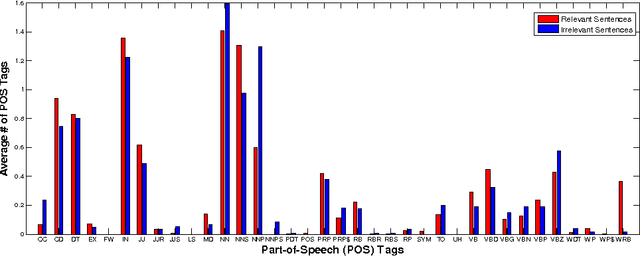
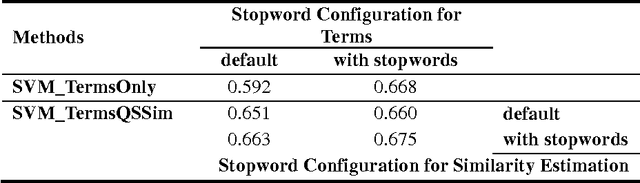
Estimating the difficulty level of math word problems is an important task for many educational applications. Identification of relevant and irrelevant sentences in math word problems is an important step for calculating the difficulty levels of such problems. This paper addresses a novel application of text categorization to identify two types of sentences in mathematical word problems, namely relevant and irrelevant sentences. A novel joint probabilistic classification model is proposed to estimate the joint probability of classification decisions for all sentences of a math word problem by utilizing the correlation among all sentences along with the correlation between the question sentence and other sentences, and sentence text. The proposed model is compared with i) a SVM classifier which makes independent classification decisions for individual sentences by only using the sentence text and ii) a novel SVM classifier that considers the correlation between the question sentence and other sentences along with the sentence text. An extensive set of experiments demonstrates the effectiveness of the joint probabilistic classification model for identifying relevant and irrelevant sentences as well as the novel SVM classifier that utilizes the correlation between the question sentence and other sentences. Furthermore, empirical results and analysis show that i) it is highly beneficial not to remove stopwords and ii) utilizing part of speech tagging does not make a significant improvement although it has been shown to be effective for the related task of math word problem type classification.