An Instrumental Value for Data Production and its Application to Data Pricing

How much value does a dataset or a data production process have to an agent who wishes to use the data to assist decision-making? This is a fundamental question towards understanding the value of data as well as further pricing of data. This paper develops an approach for capturing the instrumental value of data production processes, which takes two key factors into account: (a) the context of the agent's decision-making problem; (b) prior data or information the agent already possesses. We ''micro-found'' our valuation concepts by showing how they connect to classic notions of information design and signals in information economics. When instantiated in the domain of Bayesian linear regression, our value naturally corresponds to information gain. Based on our designed data value, we then study a basic monopoly pricing setting with a buyer looking to purchase from a seller some labeled data of a certain feature direction in order to improve a Bayesian regression model. We show that when the seller has the ability to fully customize any data request, she can extract the first-best revenue (i.e., full surplus) from any population of buyers, i.e., achieving first-degree price discrimination. If the seller can only sell data that are derived from an existing data pool, this limits her ability to customize, and achieving first-best revenue becomes generally impossible. However, we design a mechanism that achieves seller revenue at most $\log (\kappa)$ less than the first-best revenue, where $\kappa$ is the condition number associated with the data matrix. A corollary of this result is that the seller can extract the first-best revenue in the multi-armed bandits special case.

Traversing Pareto Optimal Policies: Provably Efficient Multi-Objective Reinforcement Learning

This paper investigates multi-objective reinforcement learning (MORL), which focuses on learning Pareto optimal policies in the presence of multiple reward functions. Despite MORL's significant empirical success, there is still a lack of satisfactory understanding of various MORL optimization targets and efficient learning algorithms. Our work offers a systematic analysis of several optimization targets to assess their abilities to find all Pareto optimal policies and controllability over learned policies by the preferences for different objectives. We then identify Tchebycheff scalarization as a favorable scalarization method for MORL. Considering the non-smoothness of Tchebycheff scalarization, we reformulate its minimization problem into a new min-max-max optimization problem. Then, for the stochastic policy class, we propose efficient algorithms using this reformulation to learn Pareto optimal policies. We first propose an online UCB-based algorithm to achieve an $\varepsilon$ learning error with an $\tilde{\mathcal{O}}(\varepsilon^{-2})$ sample complexity for a single given preference. To further reduce the cost of environment exploration under different preferences, we propose a preference-free framework that first explores the environment without pre-defined preferences and then generates solutions for any number of preferences. We prove that it only requires an $\tilde{\mathcal{O}}(\varepsilon^{-2})$ exploration complexity in the exploration phase and demands no additional exploration afterward. Lastly, we analyze the smooth Tchebycheff scalarization, an extension of Tchebycheff scalarization, which is proved to be more advantageous in distinguishing the Pareto optimal policies from other weakly Pareto optimal policies based on entry values of preference vectors. Furthermore, we extend our algorithms and theoretical analysis to accommodate this optimization target.

Pessimism Meets Risk: Risk-Sensitive Offline Reinforcement Learning

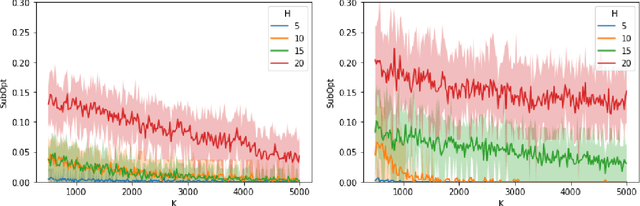
We study risk-sensitive reinforcement learning (RL), a crucial field due to its ability to enhance decision-making in scenarios where it is essential to manage uncertainty and minimize potential adverse outcomes. Particularly, our work focuses on applying the entropic risk measure to RL problems. While existing literature primarily investigates the online setting, there remains a large gap in understanding how to efficiently derive a near-optimal policy based on this risk measure using only a pre-collected dataset. We center on the linear Markov Decision Process (MDP) setting, a well-regarded theoretical framework that has yet to be examined from a risk-sensitive standpoint. In response, we introduce two provably sample-efficient algorithms. We begin by presenting a risk-sensitive pessimistic value iteration algorithm, offering a tight analysis by leveraging the structure of the risk-sensitive performance measure. To further improve the obtained bounds, we propose another pessimistic algorithm that utilizes variance information and reference-advantage decomposition, effectively improving both the dependence on the space dimension $d$ and the risk-sensitivity factor. To the best of our knowledge, we obtain the first provably efficient risk-sensitive offline RL algorithms.

Addressing Budget Allocation and Revenue Allocation in Data Market Environments Using an Adaptive Sampling Algorithm

High-quality machine learning models are dependent on access to high-quality training data. When the data are not already available, it is tedious and costly to obtain them. Data markets help with identifying valuable training data: model consumers pay to train a model, the market uses that budget to identify data and train the model (the budget allocation problem), and finally the market compensates data providers according to their data contribution (revenue allocation problem). For example, a bank could pay the data market to access data from other financial institutions to train a fraud detection model. Compensating data contributors requires understanding data's contribution to the model; recent efforts to solve this revenue allocation problem based on the Shapley value are inefficient to lead to practical data markets. In this paper, we introduce a new algorithm to solve budget allocation and revenue allocation problems simultaneously in linear time. The new algorithm employs an adaptive sampling process that selects data from those providers who are contributing the most to the model. Better data means that the algorithm accesses those providers more often, and more frequent accesses corresponds to higher compensation. Furthermore, the algorithm can be deployed in both centralized and federated scenarios, boosting its applicability. We provide theoretical guarantees for the algorithm that show the budget is used efficiently and the properties of revenue allocation are similar to Shapley's. Finally, we conduct an empirical evaluation to show the performance of the algorithm in practical scenarios and when compared to other baselines. Overall, we believe that the new algorithm paves the way for the implementation of practical data markets.

Pairwise Ranking Losses of Click-Through Rates Prediction for Welfare Maximization in Ad Auctions

We study the design of loss functions for click-through rates (CTR) to optimize (social) welfare in advertising auctions. Existing works either only focus on CTR predictions without consideration of business objectives (e.g., welfare) in auctions or assume that the distribution over the participants' expected cost-per-impression (eCPM) is known a priori, then use various additional assumptions on the parametric form of the distribution to derive loss functions for predicting CTRs. In this work, we bring back the welfare objectives of ad auctions into CTR predictions and propose a novel weighted rankloss to train the CTR model. Compared to existing literature, our approach provides a provable guarantee on welfare but without assumptions on the eCPMs' distribution while also avoiding the intractability of naively applying existing learning-to-rank methods. Further, we propose a theoretically justifiable technique for calibrating the losses using labels generated from a teacher network, only assuming that the teacher network has bounded $\ell_2$ generalization error. Finally, we demonstrate the advantages of the proposed loss on synthetic and real-world data.

A Reinforcement Learning Approach in Multi-Phase Second-Price Auction Design

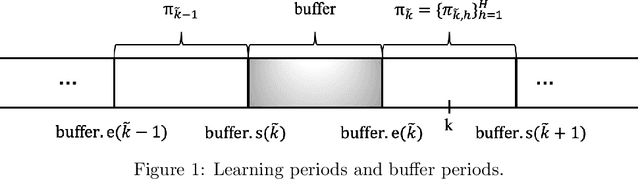
We study reserve price optimization in multi-phase second price auctions, where seller's prior actions affect the bidders' later valuations through a Markov Decision Process (MDP). Compared to the bandit setting in existing works, the setting in ours involves three challenges. First, from the seller's perspective, we need to efficiently explore the environment in the presence of potentially nontruthful bidders who aim to manipulates seller's policy. Second, we want to minimize the seller's revenue regret when the market noise distribution is unknown. Third, the seller's per-step revenue is unknown, nonlinear, and cannot even be directly observed from the environment. We propose a mechanism addressing all three challenges. To address the first challenge, we use a combination of a new technique named "buffer periods" and inspirations from Reinforcement Learning (RL) with low switching cost to limit bidders' surplus from untruthful bidding, thereby incentivizing approximately truthful bidding. The second one is tackled by a novel algorithm that removes the need for pure exploration when the market noise distribution is unknown. The third challenge is resolved by an extension of LSVI-UCB, where we use the auction's underlying structure to control the uncertainty of the revenue function. The three techniques culminate in the $\underline{\rm C}$ontextual-$\underline{\rm L}$SVI-$\underline{\rm U}$CB-$\underline{\rm B}$uffer (CLUB) algorithm which achieves $\tilde{ \mathcal{O}}(H^{5/2}\sqrt{K})$ revenue regret when the market noise is known and $\tilde{ \mathcal{O}}(H^{3}\sqrt{K})$ revenue regret when the noise is unknown with no assumptions on bidders' truthfulness.

One Policy is Enough: Parallel Exploration with a Single Policy is Minimax Optimal for Reward-Free Reinforcement Learning

While parallelism has been extensively used in Reinforcement Learning (RL), the quantitative effects of parallel exploration are not well understood theoretically. We study the benefits of simple parallel exploration for reward-free RL for linear Markov decision processes (MDPs) and two-player zero-sum Markov games (MGs). In contrast to the existing literature focused on approaches that encourage agents to explore over a diverse set of policies, we show that using a single policy to guide exploration across all agents is sufficient to obtain an almost-linear speedup in all cases compared to their fully sequential counterpart. Further, we show that this simple procedure is minimax optimal up to logarithmic factors in the reward-free setting for both linear MDPs and two-player zero-sum MGs. From a practical perspective, our paper shows that a single policy is sufficient and provably optimal for incorporating parallelism during the exploration phase.

Pessimism meets VCG: Learning Dynamic Mechanism Design via Offline Reinforcement Learning

Dynamic mechanism design has garnered significant attention from both computer scientists and economists in recent years. By allowing agents to interact with the seller over multiple rounds, where agents' reward functions may change with time and are state dependent, the framework is able to model a rich class of real world problems. In these works, the interaction between agents and sellers are often assumed to follow a Markov Decision Process (MDP). We focus on the setting where the reward and transition functions of such an MDP are not known a priori, and we are attempting to recover the optimal mechanism using an a priori collected data set. In the setting where the function approximation is employed to handle large state spaces, with only mild assumptions on the expressiveness of the function class, we are able to design a dynamic mechanism using offline reinforcement learning algorithms. Moreover, learned mechanisms approximately have three key desiderata: efficiency, individual rationality, and truthfulness. Our algorithm is based on the pessimism principle and only requires a mild assumption on the coverage of the offline data set. To the best of our knowledge, our work provides the first offline RL algorithm for dynamic mechanism design without assuming uniform coverage.

Personalized Federated Learning with Multiple Known Clusters

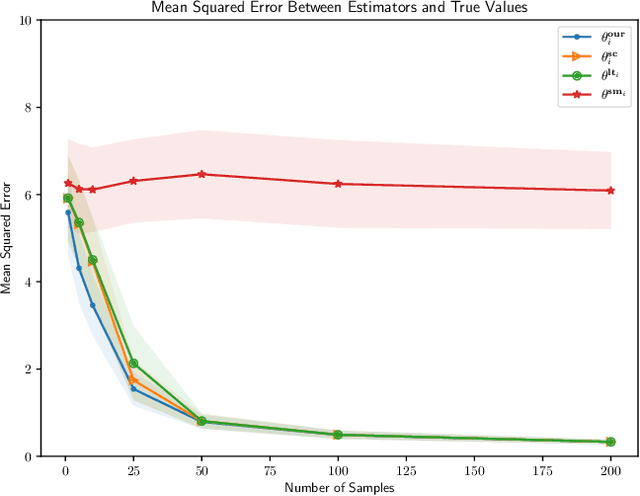
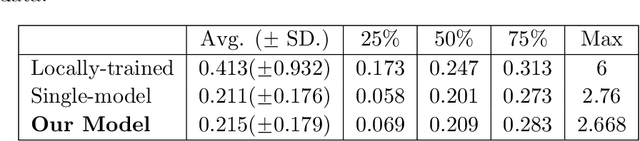
We consider the problem of personalized federated learning when there are known cluster structures within users. An intuitive approach would be to regularize the parameters so that users in the same cluster share similar model weights. The distances between the clusters can then be regularized to reflect the similarity between different clusters of users. We develop an algorithm that allows each cluster to communicate independently and derive the convergence results. We study a hierarchical linear model to theoretically demonstrate that our approach outperforms agents learning independently and agents learning a single shared weight. Finally, we demonstrate the advantages of our approach using both simulated and real-world data.

Learning Dynamic Mechanisms in Unknown Environments: A Reinforcement Learning Approach

Dynamic mechanism design studies how mechanism designers should allocate resources among agents in a time-varying environment. We consider the problem where the agents interact with the mechanism designer according to an unknown Markov Decision Process (MDP), where agent rewards and the mechanism designer's state evolve according to an episodic MDP with unknown reward functions and transition kernels. We focus on the online setting with linear function approximation and attempt to recover the dynamic Vickrey-Clarke-Grove (VCG) mechanism over multiple rounds of interaction. A key contribution of our work is incorporating reward-free online Reinforcement Learning (RL) to aid exploration over a rich policy space to estimate prices in the dynamic VCG mechanism. We show that the regret of our proposed method is upper bounded by $\tilde{\mathcal{O}}(T^{2/3})$ and further devise a lower bound to show that our algorithm is efficient, incurring the same $\tilde{\mathcal{O}}(T^{2 / 3})$ regret as the lower bound, where $T$ is the total number of rounds. Our work establishes the regret guarantee for online RL in solving dynamic mechanism design problems without prior knowledge of the underlying model.