Personalized Federated Learning with Multiple Known Clusters

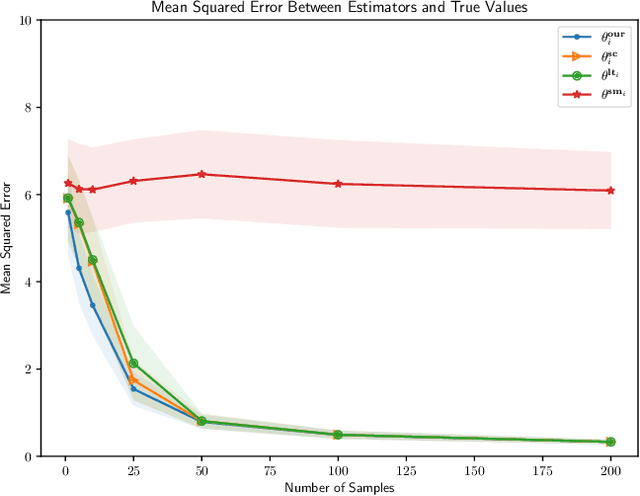
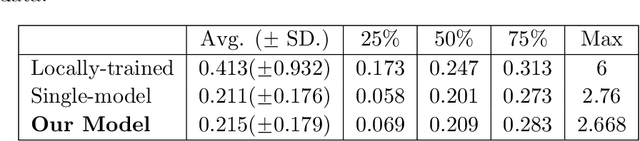
We consider the problem of personalized federated learning when there are known cluster structures within users. An intuitive approach would be to regularize the parameters so that users in the same cluster share similar model weights. The distances between the clusters can then be regularized to reflect the similarity between different clusters of users. We develop an algorithm that allows each cluster to communicate independently and derive the convergence results. We study a hierarchical linear model to theoretically demonstrate that our approach outperforms agents learning independently and agents learning a single shared weight. Finally, we demonstrate the advantages of our approach using both simulated and real-world data.

A Field Guide to Federated Optimization

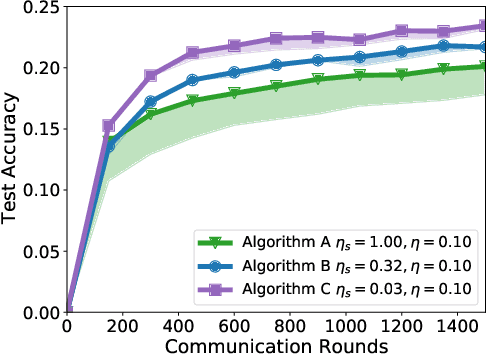
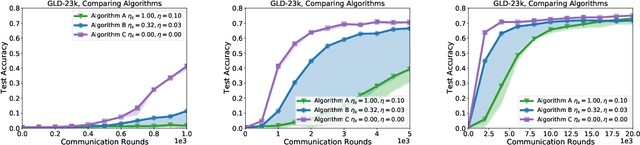
Federated learning and analytics are a distributed approach for collaboratively learning models (or statistics) from decentralized data, motivated by and designed for privacy protection. The distributed learning process can be formulated as solving federated optimization problems, which emphasize communication efficiency, data heterogeneity, compatibility with privacy and system requirements, and other constraints that are not primary considerations in other problem settings. This paper provides recommendations and guidelines on formulating, designing, evaluating and analyzing federated optimization algorithms through concrete examples and practical implementation, with a focus on conducting effective simulations to infer real-world performance. The goal of this work is not to survey the current literature, but to inspire researchers and practitioners to design federated learning algorithms that can be used in various practical applications.

Personalized Federated Learning: A Unified Framework and Universal Optimization Techniques

We study the optimization aspects of personalized Federated Learning (FL). We develop a universal optimization theory applicable to all convex personalized FL models in the literature. In particular, we propose a general personalized objective capable of recovering essentially any existing personalized FL objective as a special case. We design several optimization techniques to minimize the general objective, namely a tailored variant of Local SGD and variants of accelerated coordinate descent/accelerated SVRCD. We demonstrate the practicality and/or optimality of our methods both in terms of communication and local computation. Lastly, we argue about the implications of our general optimization theory when applied to solve specific personalized FL objectives.

Smoothness Matrices Beat Smoothness Constants: Better Communication Compression Techniques for Distributed Optimization

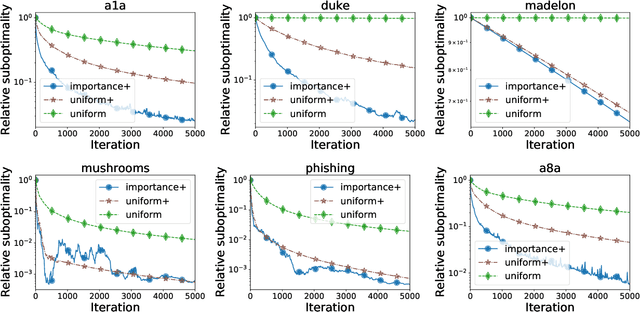
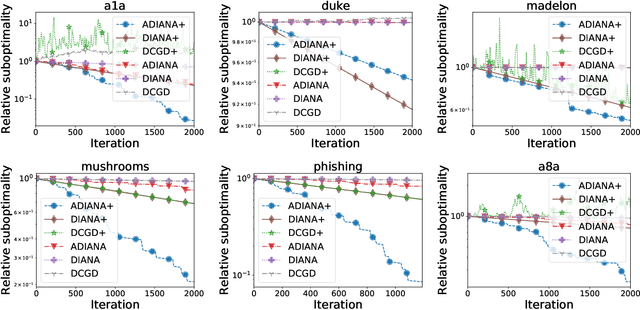
Large scale distributed optimization has become the default tool for the training of supervised machine learning models with a large number of parameters and training data. Recent advancements in the field provide several mechanisms for speeding up the training, including {\em compressed communication}, {\em variance reduction} and {\em acceleration}. However, none of these methods is capable of exploiting the inherently rich data-dependent smoothness structure of the local losses beyond standard smoothness constants. In this paper, we argue that when training supervised models, {\em smoothness matrices} -- information-rich generalizations of the ubiquitous smoothness constants -- can and should be exploited for further dramatic gains, both in theory and practice. In order to further alleviate the communication burden inherent in distributed optimization, we propose a novel communication sparsification strategy that can take full advantage of the smoothness matrices associated with local losses. To showcase the power of this tool, we describe how our sparsification technique can be adapted to three distributed optimization algorithms -- DCGD, DIANA and ADIANA -- yielding significant savings in terms of communication complexity. The new methods always outperform the baselines, often dramatically so.

Local SGD: Unified Theory and New Efficient Methods

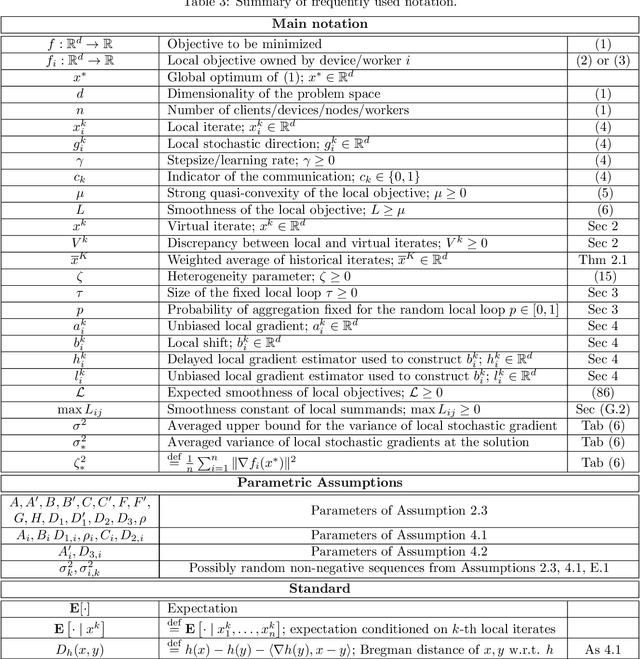
We present a unified framework for analyzing local SGD methods in the convex and strongly convex regimes for distributed/federated training of supervised machine learning models. We recover several known methods as a special case of our general framework, including Local-SGD/FedAvg, SCAFFOLD, and several variants of SGD not originally designed for federated learning. Our framework covers both the identical and heterogeneous data settings, supports both random and deterministic number of local steps, and can work with a wide array of local stochastic gradient estimators, including shifted estimators which are able to adjust the fixed points of local iterations for faster convergence. As an application of our framework, we develop multiple novel FL optimizers which are superior to existing methods. In particular, we develop the first linearly converging local SGD method which does not require any data homogeneity or other strong assumptions.

Lower Bounds and Optimal Algorithms for Personalized Federated Learning

In this work, we consider the optimization formulation of personalized federated learning recently introduced by Hanzely and Richt\'arik (2020) which was shown to give an alternative explanation to the workings of local {\tt SGD} methods. Our first contribution is establishing the first lower bounds for this formulation, for both the communication complexity and the local oracle complexity. Our second contribution is the design of several optimal methods matching these lower bounds in almost all regimes. These are the first provably optimal methods for personalized federated learning. Our optimal methods include an accelerated variant of {\tt FedProx}, and an accelerated variance-reduced version of {\tt FedAvg}/Local {\tt SGD}. We demonstrate the practical superiority of our methods through extensive numerical experiments.

Optimization for Supervised Machine Learning: Randomized Algorithms for Data and Parameters

Many key problems in machine learning and data science are routinely modeled as optimization problems and solved via optimization algorithms. With the increase of the volume of data and the size and complexity of the statistical models used to formulate these often ill-conditioned optimization tasks, there is a need for new efficient algorithms able to cope with these challenges. In this thesis, we deal with each of these sources of difficulty in a different way. To efficiently address the big data issue, we develop new methods which in each iteration examine a small random subset of the training data only. To handle the big model issue, we develop methods which in each iteration update a random subset of the model parameters only. Finally, to deal with ill-conditioned problems, we devise methods that incorporate either higher-order information or Nesterov's acceleration/momentum. In all cases, randomness is viewed as a powerful algorithmic tool that we tune, both in theory and in experiments, to achieve the best results. Our algorithms have their primary application in training supervised machine learning models via regularized empirical risk minimization, which is the dominant paradigm for training such models. However, due to their generality, our methods can be applied in many other fields, including but not limited to data science, engineering, scientific computing, and statistics.

Stochastic Subspace Cubic Newton Method

In this paper, we propose a new randomized second-order optimization algorithm---Stochastic Subspace Cubic Newton (SSCN)---for minimizing a high dimensional convex function $f$. Our method can be seen both as a {\em stochastic} extension of the cubically-regularized Newton method of Nesterov and Polyak (2006), and a {\em second-order} enhancement of stochastic subspace descent of Kozak et al. (2019). We prove that as we vary the minibatch size, the global convergence rate of SSCN interpolates between the rate of stochastic coordinate descent (CD) and the rate of cubic regularized Newton, thus giving new insights into the connection between first and second-order methods. Remarkably, the local convergence rate of SSCN matches the rate of stochastic subspace descent applied to the problem of minimizing the quadratic function $\frac12 (x-x^*)^\top \nabla^2f(x^*)(x-x^*)$, where $x^*$ is the minimizer of $f$, and hence depends on the properties of $f$ at the optimum only. Our numerical experiments show that SSCN outperforms non-accelerated first-order CD algorithms while being competitive to their accelerated variants.

Federated Learning of a Mixture of Global and Local Models

We propose a new optimization formulation for training federated learning models. The standard formulation has the form of an empirical risk minimization problem constructed to find a single global model trained from the private data stored across all participating devices. In contrast, our formulation seeks an explicit trade-off between this traditional global model and the local models, which can be learned by each device from its own private data without any communication. Further, we develop several efficient variants of SGD (with and without partial participation and with and without variance reduction) for solving the new formulation and prove communication complexity guarantees. Notably, our methods are similar but not identical to federated averaging / local SGD, thus shedding some light on the essence of the elusive method. In particular, our methods do not perform full averaging steps and instead merely take steps towards averaging. We argue for the benefits of this new paradigm for federated learning.

Variance Reduced Coordinate Descent with Acceleration: New Method With a Surprising Application to Finite-Sum Problems

We propose an accelerated version of stochastic variance reduced coordinate descent -- ASVRCD. As other variance reduced coordinate descent methods such as SEGA or SVRCD, our method can deal with problems that include a non-separable and non-smooth regularizer, while accessing a random block of partial derivatives in each iteration only. However, ASVRCD incorporates Nesterov's momentum, which offers favorable iteration complexity guarantees over both SEGA and SVRCD. As a by-product of our theory, we show that a variant of Allen-Zhu (2017) is a specific case of ASVRCD, recovering the optimal oracle complexity for the finite sum objective.