Thanos: A Block-wise Pruning Algorithm for Efficient Large Language Model Compression

This paper presents Thanos, a novel weight-pruning algorithm designed to reduce the memory footprint and enhance the computational efficiency of large language models (LLMs) by removing redundant weights while maintaining accuracy. Thanos introduces a block-wise pruning strategy with adaptive masks that dynamically adjust to weight importance, enabling flexible sparsity patterns and structured formats, such as $n:m$ sparsity, optimized for hardware acceleration. Experimental evaluations demonstrate that Thanos achieves state-of-the-art performance in structured pruning and outperforms existing methods in unstructured pruning. By providing an efficient and adaptable approach to model compression, Thanos offers a practical solution for deploying large models in resource-constrained environments.

Double Momentum and Error Feedback for Clipping with Fast Rates and Differential Privacy

Strong Differential Privacy (DP) and Optimization guarantees are two desirable properties for a method in Federated Learning (FL). However, existing algorithms do not achieve both properties at once: they either have optimal DP guarantees but rely on restrictive assumptions such as bounded gradients/bounded data heterogeneity, or they ensure strong optimization performance but lack DP guarantees. To address this gap in the literature, we propose and analyze a new method called Clip21-SGD2M based on a novel combination of clipping, heavy-ball momentum, and Error Feedback. In particular, for non-convex smooth distributed problems with clients having arbitrarily heterogeneous data, we prove that Clip21-SGD2M has optimal convergence rate and also near optimal (local-)DP neighborhood. Our numerical experiments on non-convex logistic regression and training of neural networks highlight the superiority of Clip21-SGD2M over baselines in terms of the optimization performance for a given DP-budget.

MicroAdam: Accurate Adaptive Optimization with Low Space Overhead and Provable Convergence

We propose a new variant of the Adam optimizer [Kingma and Ba, 2014] called MICROADAM that specifically minimizes memory overheads, while maintaining theoretical convergence guarantees. We achieve this by compressing the gradient information before it is fed into the optimizer state, thereby reducing its memory footprint significantly. We control the resulting compression error via a novel instance of the classical error feedback mechanism from distributed optimization [Seide et al., 2014, Alistarh et al., 2018, Karimireddy et al., 2019] in which the error correction information is itself compressed to allow for practical memory gains. We prove that the resulting approach maintains theoretical convergence guarantees competitive to those of AMSGrad, while providing good practical performance. Specifically, we show that MICROADAM can be implemented efficiently on GPUs: on both million-scale (BERT) and billion-scale (LLaMA) models, MicroAdam provides practical convergence competitive to that of the uncompressed Adam baseline, with lower memory usage and similar running time. Our code is available at https://github.com/IST-DASLab/MicroAdam.

PV-Tuning: Beyond Straight-Through Estimation for Extreme LLM Compression

There has been significant interest in "extreme" compression of large language models (LLMs), i.e., to 1-2 bits per parameter, which allows such models to be executed efficiently on resource-constrained devices. Existing work focused on improved one-shot quantization techniques and weight representations; yet, purely post-training approaches are reaching diminishing returns in terms of the accuracy-vs-bit-width trade-off. State-of-the-art quantization methods such as QuIP# and AQLM include fine-tuning (part of) the compressed parameters over a limited amount of calibration data; however, such fine-tuning techniques over compressed weights often make exclusive use of straight-through estimators (STE), whose performance is not well-understood in this setting. In this work, we question the use of STE for extreme LLM compression, showing that it can be sub-optimal, and perform a systematic study of quantization-aware fine-tuning strategies for LLMs. We propose PV-Tuning - a representation-agnostic framework that generalizes and improves upon existing fine-tuning strategies, and provides convergence guarantees in restricted cases. On the practical side, when used for 1-2 bit vector quantization, PV-Tuning outperforms prior techniques for highly-performant models such as Llama and Mistral. Using PV-Tuning, we achieve the first Pareto-optimal quantization for Llama 2 family models at 2 bits per parameter.

Federated Learning is Better with Non-Homomorphic Encryption

Traditional AI methodologies necessitate centralized data collection, which becomes impractical when facing problems with network communication, data privacy, or storage capacity. Federated Learning (FL) offers a paradigm that empowers distributed AI model training without collecting raw data. There are different choices for providing privacy during FL training. One of the popular methodologies is employing Homomorphic Encryption (HE) - a breakthrough in privacy-preserving computation from Cryptography. However, these methods have a price in the form of extra computation and memory footprint. To resolve these issues, we propose an innovative framework that synergizes permutation-based compressors with Classical Cryptography, even though employing Classical Cryptography was assumed to be impossible in the past in the context of FL. Our framework offers a way to replace HE with cheaper Classical Cryptography primitives which provides security for the training process. It fosters asynchronous communication and provides flexible deployment options in various communication topologies.

Adaptive Compression for Communication-Efficient Distributed Training

We propose Adaptive Compressed Gradient Descent (AdaCGD) - a novel optimization algorithm for communication-efficient training of supervised machine learning models with adaptive compression level. Our approach is inspired by the recently proposed three point compressor (3PC) framework of Richtarik et al. (2022), which includes error feedback (EF21), lazily aggregated gradient (LAG), and their combination as special cases, and offers the current state-of-the-art rates for these methods under weak assumptions. While the above mechanisms offer a fixed compression level, or adapt between two extremes only, our proposal is to perform a much finer adaptation. In particular, we allow the user to choose any number of arbitrarily chosen contractive compression mechanisms, such as Top-K sparsification with a user-defined selection of sparsification levels K, or quantization with a user-defined selection of quantization levels, or their combination. AdaCGD chooses the appropriate compressor and compression level adaptively during the optimization process. Besides i) proposing a theoretically-grounded multi-adaptive communication compression mechanism, we further ii) extend the 3PC framework to bidirectional compression, i.e., we allow the server to compress as well, and iii) provide sharp convergence bounds in the strongly convex, convex and nonconvex settings. The convex regime results are new even for several key special cases of our general mechanism, including 3PC and EF21. In all regimes, our rates are superior compared to all existing adaptive compression methods.

Convergence of Stein Variational Gradient Descent under a Weaker Smoothness Condition

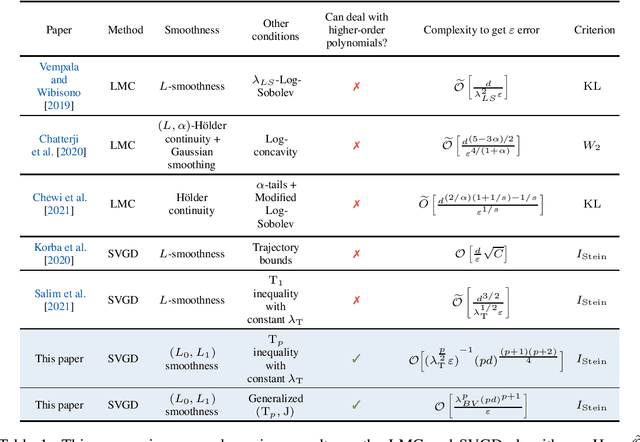
Stein Variational Gradient Descent (SVGD) is an important alternative to the Langevin-type algorithms for sampling from probability distributions of the form $\pi(x) \propto \exp(-V(x))$. In the existing theory of Langevin-type algorithms and SVGD, the potential function $V$ is often assumed to be $L$-smooth. However, this restrictive condition excludes a large class of potential functions such as polynomials of degree greater than $2$. Our paper studies the convergence of the SVGD algorithm for distributions with $(L_0,L_1)$-smooth potentials. This relaxed smoothness assumption was introduced by Zhang et al. [2019a] for the analysis of gradient clipping algorithms. With the help of trajectory-independent auxiliary conditions, we provide a descent lemma establishing that the algorithm decreases the $\mathrm{KL}$ divergence at each iteration and prove a complexity bound for SVGD in the population limit in terms of the Stein Fisher information.

A Field Guide to Federated Optimization

Federated learning and analytics are a distributed approach for collaboratively learning models (or statistics) from decentralized data, motivated by and designed for privacy protection. The distributed learning process can be formulated as solving federated optimization problems, which emphasize communication efficiency, data heterogeneity, compatibility with privacy and system requirements, and other constraints that are not primary considerations in other problem settings. This paper provides recommendations and guidelines on formulating, designing, evaluating and analyzing federated optimization algorithms through concrete examples and practical implementation, with a focus on conducting effective simulations to infer real-world performance. The goal of this work is not to survey the current literature, but to inspire researchers and practitioners to design federated learning algorithms that can be used in various practical applications.

A Linearly Convergent Algorithm for Decentralized Optimization: Sending Less Bits for Free!

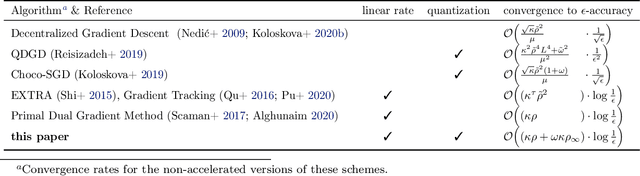
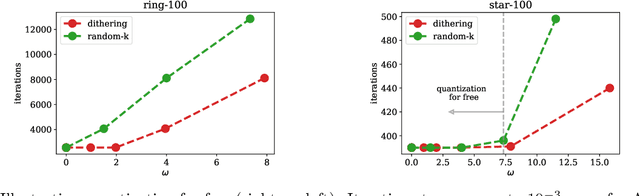
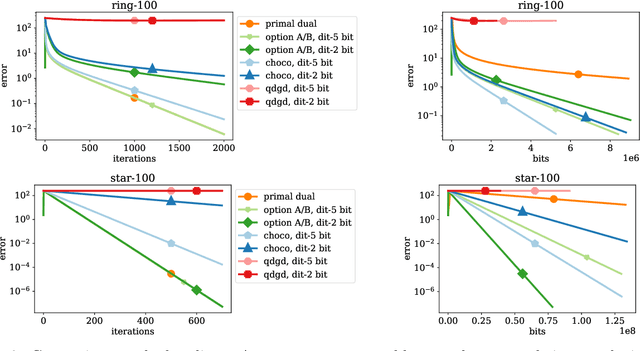
Decentralized optimization methods enable on-device training of machine learning models without a central coordinator. In many scenarios communication between devices is energy demanding and time consuming and forms the bottleneck of the entire system. We propose a new randomized first-order method which tackles the communication bottleneck by applying randomized compression operators to the communicated messages. By combining our scheme with a new variance reduction technique that progressively throughout the iterations reduces the adverse effect of the injected quantization noise, we obtain the first scheme that converges linearly on strongly convex decentralized problems while using compressed communication only. We prove that our method can solve the problems without any increase in the number of communications compared to the baseline which does not perform any communication compression while still allowing for a significant compression factor which depends on the conditioning of the problem and the topology of the network. Our key theoretical findings are supported by numerical experiments.

Optimal Client Sampling for Federated Learning

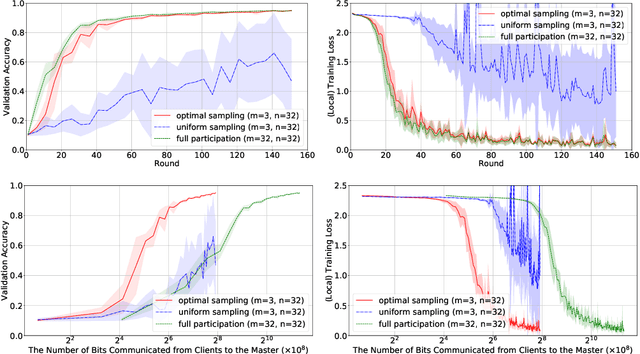
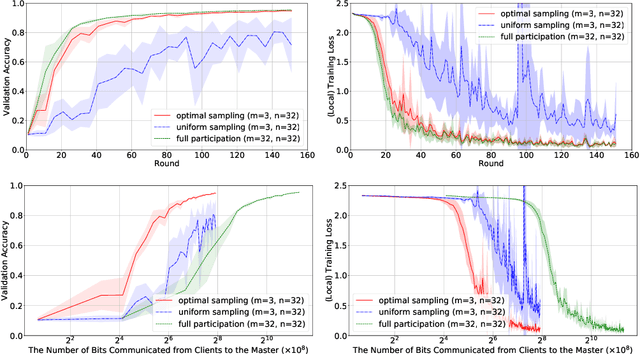
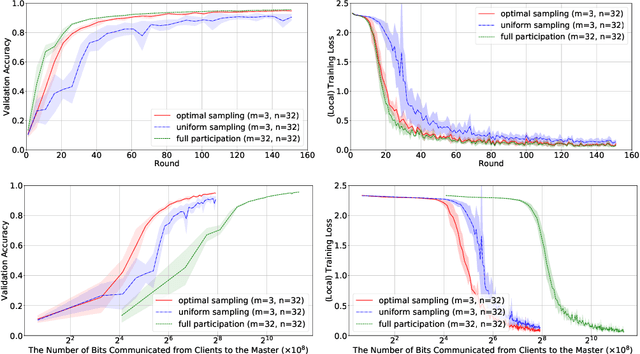
It is well understood that client-master communication can be a primary bottleneck in Federated Learning. In this work, we address this issue with a novel client subsampling scheme, where we restrict the number of clients allowed to communicate their updates back to the master node. In each communication round, all participated clients compute their updates, but only the ones with "important" updates communicate back to the master. We show that importance can be measured using only the norm of the update and we give a formula for optimal client participation. This formula minimizes the distance between the full update, where all clients participate, and our limited update, where the number of participating clients is restricted. In addition, we provide a simple algorithm that approximates the optimal formula for client participation which only requires secure aggregation and thus does not compromise client privacy. We show both theoretically and empirically that our approach leads to superior performance for Distributed SGD (DSGD) and Federated Averaging (FedAvg) compared to the baseline where participating clients are sampled uniformly. Finally, our approach is orthogonal to and compatible with existing methods for reducing communication overhead, such as local methods and communication compression methods.