Enhancing LLM Training via Spectral Clipping

While spectral-based optimizers like Muon operate directly on the spectrum of updates, standard adaptive methods such as AdamW do not account for the global spectral structure of weights and gradients, leaving them vulnerable to two empirical issues in large language model (LLM) training: (i) the optimizer updates can have large spectral norms, potentially destabilizing training and degrading generalization; (ii) stochastic gradient noise can exhibit sparse spectral spikes, with a few dominant singular values much larger than the rest. We propose SPECTRA, a general framework addressing these by (i) post-spectral clipping of updates to enforce spectral-norm constraints; (ii) optional pre-spectral clipping of gradients to suppress spectral noise spikes. We prove that post-clipping constitutes a Composite Frank-Wolfe method with spectral-norm constraints and weight regularization, recovering Frobenius and $\ell_{\infty}$-norm regularization with SGD-based and sign-based methods. We further analyze how pre-clipping mitigates sparse spectral spikes. We propose efficient soft spectral clipping via Newton-Schulz iterations, avoiding expensive SVD. Experiments on LLM pretraining show SPECTRA uniformly improves validation loss for various optimizers, including AdamW, Signum, and AdEMAMix, with the best-performing variants achieving state-of-the-art results. Models trained with SPECTRA exhibit smaller weight norms, confirming the link between spectral clipping and regularization.

On the Stability of Nonlinear Dynamics in GD and SGD: Beyond Quadratic Potentials

The dynamical stability of the iterates during training plays a key role in determining the minima obtained by optimization algorithms. For example, stable solutions of gradient descent (GD) correspond to flat minima, which have been associated with favorable features. While prior work often relies on linearization to determine stability, it remains unclear whether linearized dynamics faithfully capture the full nonlinear behavior. Recent work has shown that GD may stably oscillate near a linearly unstable minimum and still converge once the step size decays, indicating that linear analysis can be misleading. In this work, we explicitly study the effect of nonlinear terms. Specifically, we derive an exact criterion for stable oscillations of GD near minima in the multivariate setting. Our condition depends on high-order derivatives, generalizing existing results. Extending the analysis to stochastic gradient descent (SGD), we show that nonlinear dynamics can diverge in expectation even if a single batch is unstable. This implies that stability can be dictated by a single batch that oscillates unstably, rather than an average effect, as linear analysis suggests. Finally, we prove that if all batches are linearly stable, the nonlinear dynamics of SGD are stable in expectation.

Sequential Subspace Noise Injection Prevents Accuracy Collapse in Certified Unlearning

Certified unlearning based on differential privacy offers strong guarantees but remains largely impractical: the noisy fine-tuning approaches proposed so far achieve these guarantees but severely reduce model accuracy. We propose sequential noise scheduling, which distributes the noise budget across orthogonal subspaces of the parameter space, rather than injecting it all at once. This simple modification mitigates the destructive effect of noise while preserving the original certification guarantees. We extend the analysis of noisy fine-tuning to the subspace setting, proving that the same $(\varepsilon,δ)$ privacy budget is retained. Empirical results on image classification benchmarks show that our approach substantially improves accuracy after unlearning while remaining robust to membership inference attacks. These results show that certified unlearning can achieve both rigorous guarantees and practical utility.

Exploiting Similarity for Computation and Communication-Efficient Decentralized Optimization

Reducing communication complexity is critical for efficient decentralized optimization. The proximal decentralized optimization (PDO) framework is particularly appealing, as methods within this framework can exploit functional similarity among nodes to reduce communication rounds. Specifically, when local functions at different nodes are similar, these methods achieve faster convergence with fewer communication steps. However, existing PDO methods often require highly accurate solutions to subproblems associated with the proximal operator, resulting in significant computational overhead. In this work, we propose the Stabilized Proximal Decentralized Optimization (SPDO) method, which achieves state-of-the-art communication and computational complexities within the PDO framework. Additionally, we refine the analysis of existing PDO methods by relaxing subproblem accuracy requirements and leveraging average functional similarity. Experimental results demonstrate that SPDO significantly outperforms existing methods.

Accelerated Distributed Optimization with Compression and Error Feedback

Modern machine learning tasks often involve massive datasets and models, necessitating distributed optimization algorithms with reduced communication overhead. Communication compression, where clients transmit compressed updates to a central server, has emerged as a key technique to mitigate communication bottlenecks. However, the theoretical understanding of stochastic distributed optimization with contractive compression remains limited, particularly in conjunction with Nesterov acceleration -- a cornerstone for achieving faster convergence in optimization. In this paper, we propose a novel algorithm, ADEF (Accelerated Distributed Error Feedback), which integrates Nesterov acceleration, contractive compression, error feedback, and gradient difference compression. We prove that ADEF achieves the first accelerated convergence rate for stochastic distributed optimization with contractive compression in the general convex regime. Numerical experiments validate our theoretical findings and demonstrate the practical efficacy of ADEF in reducing communication costs while maintaining fast convergence.

Scalable Decentralized Learning with Teleportation

Decentralized SGD can run with low communication costs, but its sparse communication characteristics deteriorate the convergence rate, especially when the number of nodes is large. In decentralized learning settings, communication is assumed to occur on only a given topology, while in many practical cases, the topology merely represents a preferred communication pattern, and connecting to arbitrary nodes is still possible. Previous studies have tried to alleviate the convergence rate degradation in these cases by designing topologies with large spectral gaps. However, the degradation is still significant when the number of nodes is substantial. In this work, we propose TELEPORTATION. TELEPORTATION activates only a subset of nodes, and the active nodes fetch the parameters from previous active nodes. Then, the active nodes update their parameters by SGD and perform gossip averaging on a relatively small topology comprising only the active nodes. We show that by activating only a proper number of nodes, TELEPORTATION can completely alleviate the convergence rate degradation. Furthermore, we propose an efficient hyperparameter-tuning method to search for the appropriate number of nodes to be activated. Experimentally, we showed that TELEPORTATION can train neural networks more stably and achieve higher accuracy than Decentralized SGD.

Decoupled SGDA for Games with Intermittent Strategy Communication

We focus on reducing communication overhead in multiplayer games, where frequently exchanging strategies between players is not feasible and players have noisy or outdated strategies of the other players. We introduce Decoupled SGDA, a novel adaptation of Stochastic Gradient Descent Ascent (SGDA). In this approach, players independently update their strategies based on outdated opponent strategies, with periodic synchronization to align strategies. For Strongly-Convex-Strongly-Concave (SCSC) games, we demonstrate that Decoupled SGDA achieves near-optimal communication complexity comparable to the best-known GDA rates. For weakly coupled games where the interaction between players is lower relative to the non-interactive part of the game, Decoupled SGDA significantly reduces communication costs compared to standard SGDA. Our findings extend to multi-player games. To provide insights into the effect of communication frequency and convergence, we extensively study the convergence of Decoupled SGDA for quadratic minimax problems. Lastly, in settings where the noise over the players is imbalanced, Decoupled SGDA significantly outperforms federated minimax methods.

Stabilized Proximal-Point Methods for Federated Optimization

In developing efficient optimization algorithms, it is crucial to account for communication constraints -- a significant challenge in modern federated learning settings. The best-known communication complexity among non-accelerated algorithms is achieved by DANE, a distributed proximal-point algorithm that solves local subproblems in each iteration and that can exploit second-order similarity among individual functions. However, to achieve such communication efficiency, the accuracy requirement for solving the local subproblems is slightly sub-optimal. Inspired by the hybrid projection-proximal point method, in this work, we i) propose a novel distributed algorithm S-DANE. This method adopts a more stabilized prox-center in the proximal step compared with DANE, and matches its deterministic communication complexity. Moreover, the accuracy condition of the subproblem is milder, leading to enhanced local computation efficiency. Furthermore, it supports partial client participation and arbitrary stochastic local solvers, making it more attractive in practice. We further ii) accelerate S-DANE, and show that the resulting algorithm achieves the best-known communication complexity among all existing methods for distributed convex optimization, with the same improved local computation efficiency as S-DANE.

Near Optimal Decentralized Optimization with Compression and Momentum Tracking

Communication efficiency has garnered significant attention as it is considered the main bottleneck for large-scale decentralized Machine Learning applications in distributed and federated settings. In this regime, clients are restricted to transmitting small amounts of quantized information to their neighbors over a communication graph. Numerous endeavors have been made to address this challenging problem by developing algorithms with compressed communication for decentralized non-convex optimization problems. Despite considerable efforts, the current results suffer from various issues such as non-scalability with the number of clients, requirements for large batches, or bounded gradient assumption. In this paper, we introduce MoTEF, a novel approach that integrates communication compression with Momentum Tracking and Error Feedback. Our analysis demonstrates that MoTEF achieves most of the desired properties, and significantly outperforms existing methods under arbitrary data heterogeneity. We provide numerical experiments to validate our theoretical findings and confirm the practical superiority of MoTEF.

The Limits and Potentials of Local SGD for Distributed Heterogeneous Learning with Intermittent Communication

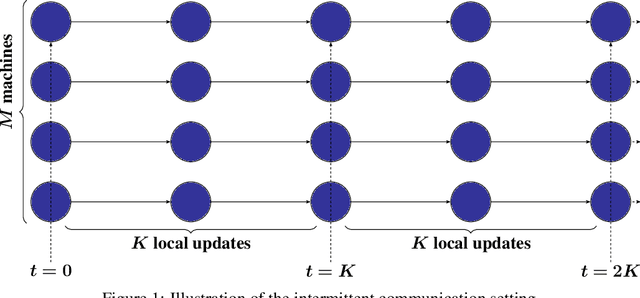
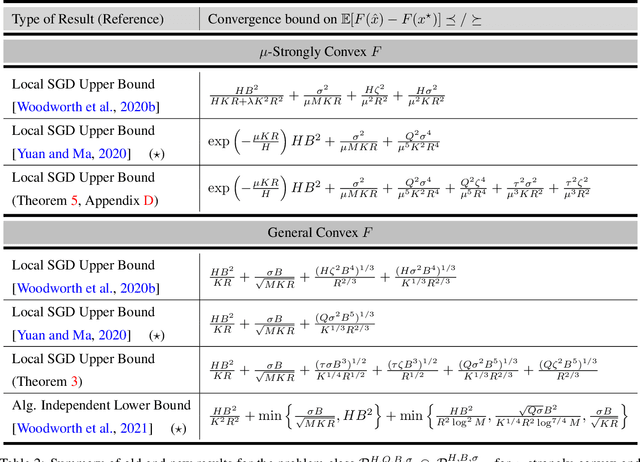
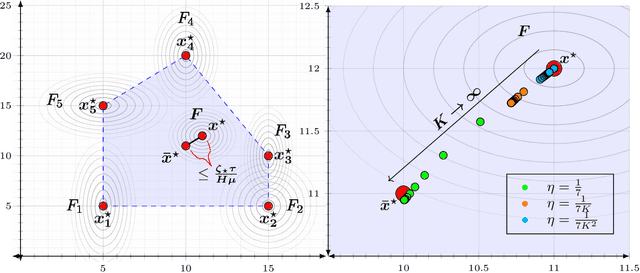
Local SGD is a popular optimization method in distributed learning, often outperforming other algorithms in practice, including mini-batch SGD. Despite this success, theoretically proving the dominance of local SGD in settings with reasonable data heterogeneity has been difficult, creating a significant gap between theory and practice. In this paper, we provide new lower bounds for local SGD under existing first-order data heterogeneity assumptions, showing that these assumptions are insufficient to prove the effectiveness of local update steps. Furthermore, under these same assumptions, we demonstrate the min-max optimality of accelerated mini-batch SGD, which fully resolves our understanding of distributed optimization for several problem classes. Our results emphasize the need for better models of data heterogeneity to understand the effectiveness of local SGD in practice. Towards this end, we consider higher-order smoothness and heterogeneity assumptions, providing new upper bounds that imply the dominance of local SGD over mini-batch SGD when data heterogeneity is low.