Learning Variational Inequalities from Data: Fast Generalization Rates under Strong Monotonicity

Variational inequalities (VIs) are a broad class of optimization problems encompassing machine learning problems ranging from standard convex minimization to more complex scenarios like min-max optimization and computing the equilibria of multi-player games. In convex optimization, strong convexity allows for fast statistical learning rates requiring only $\Theta(1/\epsilon)$ stochastic first-order oracle calls to find an $\epsilon$-optimal solution, rather than the standard $\Theta(1/\epsilon^2)$ calls. In this paper, we explain how one can similarly obtain fast $\Theta(1/\epsilon)$ rates for learning VIs that satisfy strong monotonicity, a generalization of strong convexity. Specifically, we demonstrate that standard stability-based generalization arguments for convex minimization extend directly to VIs when the domain admits a small covering, or when the operator is integrable and suboptimality is measured by potential functions; such as when finding equilibria in multi-player games.

On the Hypomonotone Class of Variational Inequalities

This paper studies the behavior of the extragradient algorithm when applied to hypomonotone operators, a class of problems that extends beyond the classical monotone setting. While the extragradient method is widely known for its efficacy in solving variational inequalities with monotone and Lipschitz continuous operators, we demonstrate that its convergence is not guaranteed in the hypomonotone setting. We provide a characterization theorem that identifies the conditions under which the extragradient algorithm fails to converge. Our results highlight the necessity of stronger assumptions to guarantee convergence of extragradient and to further develop the existing VI methods for broader problems.

Variational Inequality Methods for Multi-Agent Reinforcement Learning: Performance and Stability Gains

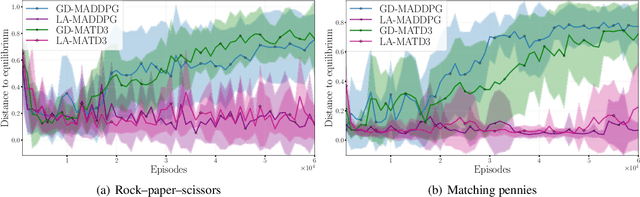
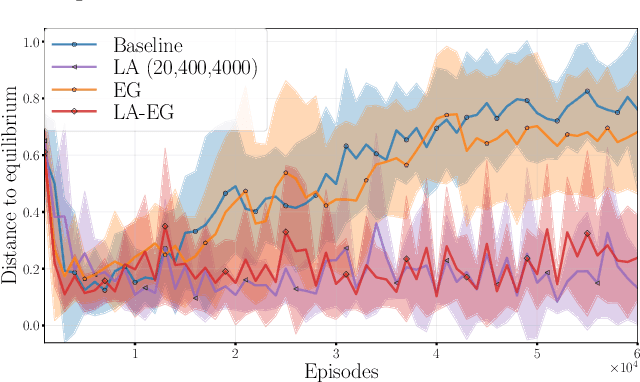
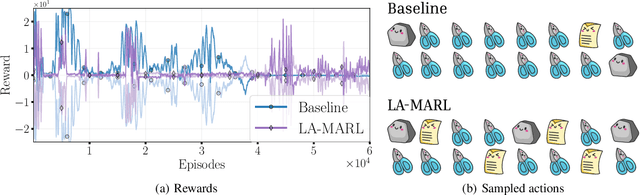
Multi-agent reinforcement learning (MARL) presents unique challenges as agents learn strategies through experiences. Gradient-based methods are often sensitive to hyperparameter selection and initial random seed variations. Concurrently, significant advances have been made in solving Variational Inequalities (VIs) which include equilibrium-finding problems particularly in addressing the non-converging rotational dynamics that impede convergence of traditional gradient based optimization methods. This paper explores the potential of leveraging VI-based techniques to improve MARL training. Specifically, we study the performance of VI method namely, Nested-Lookahead VI (nLA-VI) and Extragradient (EG) in enhancing the multi-agent deep deterministic policy gradient (MADDPG) algorithm. We present a VI reformulation of the actor-critic algorithm for both single- and multi-agent settings. We introduce three algorithms that use nLA-VI, EG, and a combination of both, named LA-MADDPG, EG-MADDPG, and LA-EG-MADDPG, respectively. Our empirical results demonstrate that these VI-based approaches yield significant performance improvements in benchmark environments, such as the zero-sum games: rock-paper-scissors and matching pennies, where equilibrium strategies can be quantitatively assessed, and the Multi-Agent Particle Environment: Predator prey benchmark, where VI-based methods also yield balanced participation of agents from the same team.

Revisiting the ACVI Method for Constrained Variational Inequalities

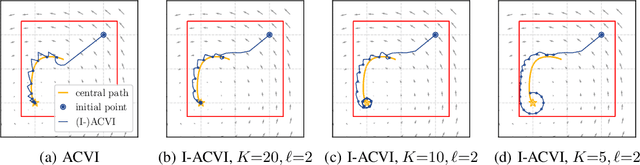
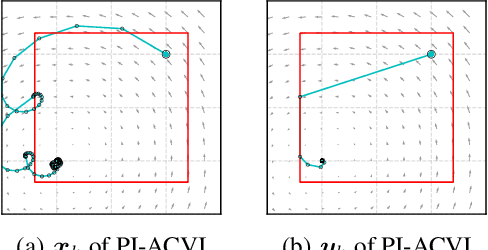
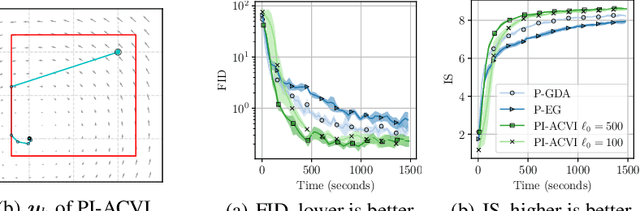
ACVI is a recently proposed first-order method for solving variational inequalities (VIs) with general constraints. Yang et al. (2022) showed that the gap function of the last iterate decreases at a rate of $\mathcal{O}(\frac{1}{\sqrt{K}})$ when the operator is $L$-Lipschitz, monotone, and at least one constraint is active. In this work, we show that the same guarantee holds when only assuming that the operator is monotone. To our knowledge, this is the first analytically derived last-iterate convergence rate for general monotone VIs, and overall the only one that does not rely on the assumption that the operator is $L$-Lipschitz. Furthermore, when the sub-problems of ACVI are solved approximately, we show that by using a standard warm-start technique the convergence rate stays the same, provided that the errors decrease at appropriate rates. We further provide empirical analyses and insights on its implementation for the latter case.

Continuous-time Analysis for Variational Inequalities: An Overview and Desiderata

Algorithms that solve zero-sum games, multi-objective agent objectives, or, more generally, variational inequality (VI) problems are notoriously unstable on general problems. Owing to the increasing need for solving such problems in machine learning, this instability has been highlighted in recent years as a significant research challenge. In this paper, we provide an overview of recent progress in the use of continuous-time perspectives in the analysis and design of methods targeting the broad VI problem class. Our presentation draws parallels between single-objective problems and multi-objective problems, highlighting the challenges of the latter. We also formulate various desiderata for algorithms that apply to general VIs and we argue that achieving these desiderata may profit from an understanding of the associated continuous-time dynamics.

Solving Constrained Variational Inequalities via an Interior Point Method

We develop an interior-point approach to solve constrained variational inequality (cVI) problems. Inspired by the efficacy of the alternating direction method of multipliers (ADMM) method in the single-objective context, we generalize ADMM to derive a first-order method for cVIs, that we refer to as ADMM-based interior point method for constrained VIs (ACVI). We provide convergence guarantees for ACVI in two general classes of problems: (i) when the operator is $\xi$-monotone, and (ii) when it is monotone, the constraints are active and the game is not purely rotational. When the operator is in addition L-Lipschitz for the latter case, we match known lower bounds on rates for the gap function of $\mathcal{O}(1/\sqrt{K})$ and $\mathcal{O}(1/K)$ for the last and average iterate, respectively. To the best of our knowledge, this is the first presentation of a first-order interior-point method for the general cVI problem that has a global convergence guarantee. Moreover, unlike previous work in this setting, ACVI provides a means to solve cVIs when the constraints are nontrivial. Empirical analyses demonstrate clear advantages of ACVI over common first-order methods. In particular, (i) cyclical behavior is notably reduced as our methods approach the solution from the analytic center, and (ii) unlike projection-based methods that oscillate when near a constraint, ACVI efficiently handles the constraints.

Improving Generalization via Uncertainty Driven Perturbations

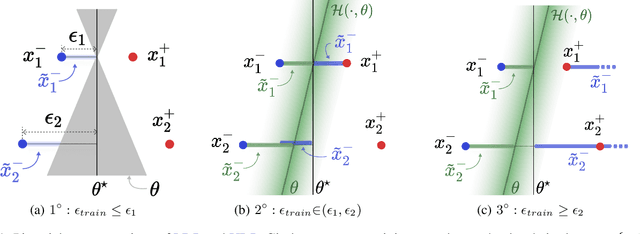
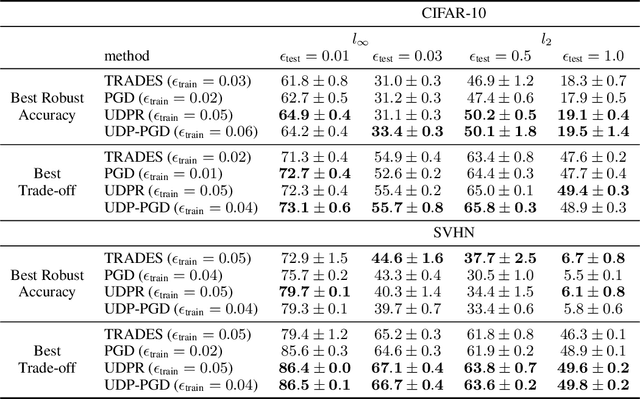
Recently Shah et al., 2020 pointed out the pitfalls of the simplicity bias - the tendency of gradient-based algorithms to learn simple models - which include the model's high sensitivity to small input perturbations, as well as sub-optimal margins. In particular, while Stochastic Gradient Descent yields max-margin boundary on linear models, such guarantee does not extend to non-linear models. To mitigate the simplicity bias, we consider uncertainty-driven perturbations (UDP) of the training data points, obtained iteratively by following the direction that maximizes the model's estimated uncertainty. The uncertainty estimate does not rely on the input's label and it is highest at the decision boundary, and - unlike loss-driven perturbations - it allows for using a larger range of values for the perturbation magnitude. Furthermore, as real-world datasets have non-isotropic distances between data points of different classes, the above property is particularly appealing for increasing the margin of the decision boundary, which in turn improves the model's generalization. We show that UDP is guaranteed to achieve the maximum margin decision boundary on linear models and that it notably increases it on challenging simulated datasets. For nonlinear models, we show empirically that UDP reduces the simplicity bias and learns more exhaustive features. Interestingly, it also achieves competitive loss-based robustness and generalization trade-off on several datasets.

Last-Iterate Convergence of Saddle Point Optimizers via High-Resolution Differential Equations

Several widely-used first-order saddle point optimization methods yield an identical continuous-time ordinary differential equation (ODE) to that of the Gradient Descent Ascent (GDA) method when derived naively. However, their convergence properties are very different even on simple bilinear games. We use a technique from fluid dynamics called High-Resolution Differential Equations (HRDEs) to design ODEs of several saddle point optimization methods. On bilinear games, the convergence properties of the derived HRDEs correspond to that of the starting discrete methods. Using these techniques, we show that the HRDE of Optimistic Gradient Descent Ascent (OGDA) has last-iterate convergence for general monotone variational inequalities. To our knowledge, this is the first continuous-time dynamics shown to converge for such a general setting. Moreover, we provide the rates for the best-iterate convergence of the OGDA method, relying solely on the first-order smoothness of the monotone operator.

The Peril of Popular Deep Learning Uncertainty Estimation Methods

Uncertainty estimation (UE) techniques -- such as the Gaussian process (GP), Bayesian neural networks (BNN), Monte Carlo dropout (MCDropout) -- aim to improve the interpretability of machine learning models by assigning an estimated uncertainty value to each of their prediction outputs. However, since too high uncertainty estimates can have fatal consequences in practice, this paper analyzes the above techniques. Firstly, we show that GP methods always yield high uncertainty estimates on out of distribution (OOD) data. Secondly, we show on a 2D toy example that both BNNs and MCDropout do not give high uncertainty estimates on OOD samples. Finally, we show empirically that this pitfall of BNNs and MCDropout holds on real world datasets as well. Our insights (i) raise awareness for the more cautious use of currently popular UE methods in Deep Learning, (ii) encourage the development of UE methods that approximate GP-based methods -- instead of BNNs and MCDropout, and (iii) our empirical setups can be used for verifying the OOD performances of any other UE method. The source code is available at https://github.com/epfml/uncertainity-estimation.

Semantic Perturbations with Normalizing Flows for Improved Generalization

Data augmentation is a widely adopted technique for avoiding overfitting when training deep neural networks. However, this approach requires domain-specific knowledge and is often limited to a fixed set of hard-coded transformations. Recently, several works proposed to use generative models for generating semantically meaningful perturbations to train a classifier. However, because accurate encoding and decoding are critical, these methods, which use architectures that approximate the latent-variable inference, remained limited to pilot studies on small datasets. Exploiting the exactly reversible encoder-decoder structure of normalizing flows, we perform on-manifold perturbations in the latent space to define fully unsupervised data augmentations. We demonstrate that such perturbations match the performance of advanced data augmentation techniques -- reaching 96.6% test accuracy for CIFAR-10 using ResNet-18 and outperform existing methods, particularly in low data regimes -- yielding 10--25% relative improvement of test accuracy from classical training. We find that our latent adversarial perturbations adaptive to the classifier throughout its training are most effective, yielding the first test accuracy improvement results on real-world datasets -- CIFAR-10/100 -- via latent-space perturbations.