Provable Maximum Entropy Manifold Exploration via Diffusion Models

Exploration is critical for solving real-world decision-making problems such as scientific discovery, where the objective is to generate truly novel designs rather than mimic existing data distributions. In this work, we address the challenge of leveraging the representational power of generative models for exploration without relying on explicit uncertainty quantification. We introduce a novel framework that casts exploration as entropy maximization over the approximate data manifold implicitly defined by a pre-trained diffusion model. Then, we present a novel principle for exploration based on density estimation, a problem well-known to be challenging in practice. To overcome this issue and render this method truly scalable, we leverage a fundamental connection between the entropy of the density induced by a diffusion model and its score function. Building on this, we develop an algorithm based on mirror descent that solves the exploration problem as sequential fine-tuning of a pre-trained diffusion model. We prove its convergence to the optimal exploratory diffusion model under realistic assumptions by leveraging recent understanding of mirror flows. Finally, we empirically evaluate our approach on both synthetic and high-dimensional text-to-image diffusion, demonstrating promising results.

Sinkhorn Flow: A Continuous-Time Framework for Understanding and Generalizing the Sinkhorn Algorithm

Many problems in machine learning can be formulated as solving entropy-regularized optimal transport on the space of probability measures. The canonical approach involves the Sinkhorn iterates, renowned for their rich mathematical properties. Recently, the Sinkhorn algorithm has been recast within the mirror descent framework, thus benefiting from classical optimization theory insights. Here, we build upon this result by introducing a continuous-time analogue of the Sinkhorn algorithm. This perspective allows us to derive novel variants of Sinkhorn schemes that are robust to noise and bias. Moreover, our continuous-time dynamics not only generalize but also offer a unified perspective on several recently discovered dynamics in machine learning and mathematics, such as the "Wasserstein mirror flow" of (Deb et al. 2023) or the "mean-field Schr\"odinger equation" of (Claisse et al. 2023).

Riemannian stochastic optimization methods avoid strict saddle points

Many modern machine learning applications - from online principal component analysis to covariance matrix identification and dictionary learning - can be formulated as minimization problems on Riemannian manifolds, and are typically solved with a Riemannian stochastic gradient method (or some variant thereof). However, in many cases of interest, the resulting minimization problem is not geodesically convex, so the convergence of the chosen solver to a desirable solution - i.e., a local minimizer - is by no means guaranteed. In this paper, we study precisely this question, that is, whether stochastic Riemannian optimization algorithms are guaranteed to avoid saddle points with probability 1. For generality, we study a family of retraction-based methods which, in addition to having a potentially much lower per-iteration cost relative to Riemannian gradient descent, include other widely used algorithms, such as natural policy gradient methods and mirror descent in ordinary convex spaces. In this general setting, we show that, under mild assumptions for the ambient manifold and the oracle providing gradient information, the policies under study avoid strict saddle points / submanifolds with probability 1, from any initial condition. This result provides an important sanity check for the use of gradient methods on manifolds as it shows that, almost always, the limit state of a stochastic Riemannian algorithm can only be a local minimizer.

Unbalanced Diffusion Schrödinger Bridge

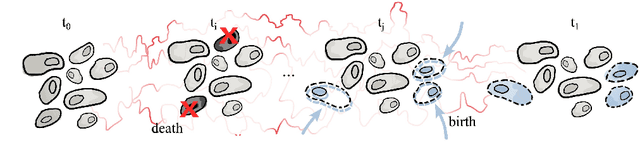
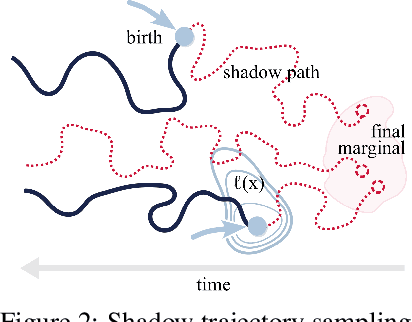
Schr\"odinger bridges (SBs) provide an elegant framework for modeling the temporal evolution of populations in physical, chemical, or biological systems. Such natural processes are commonly subject to changes in population size over time due to the emergence of new species or birth and death events. However, existing neural parameterizations of SBs such as diffusion Schr\"odinger bridges (DSBs) are restricted to settings in which the endpoints of the stochastic process are both probability measures and assume conservation of mass constraints. To address this limitation, we introduce unbalanced DSBs which model the temporal evolution of marginals with arbitrary finite mass. This is achieved by deriving the time reversal of stochastic differential equations with killing and birth terms. We present two novel algorithmic schemes that comprise a scalable objective function for training unbalanced DSBs and provide a theoretical analysis alongside challenging applications on predicting heterogeneous molecular single-cell responses to various cancer drugs and simulating the emergence and spread of new viral variants.

Aligned Diffusion Schrödinger Bridges

Diffusion Schr\"odinger bridges (DSB) have recently emerged as a powerful framework for recovering stochastic dynamics via their marginal observations at different time points. Despite numerous successful applications, existing algorithms for solving DSBs have so far failed to utilize the structure of aligned data, which naturally arises in many biological phenomena. In this paper, we propose a novel algorithmic framework that, for the first time, solves DSBs while respecting the data alignment. Our approach hinges on a combination of two decades-old ideas: The classical Schr\"odinger bridge theory and Doob's $h$-transform. Compared to prior methods, our approach leads to a simpler training procedure with lower variance, which we further augment with principled regularization schemes. This ultimately leads to sizeable improvements across experiments on synthetic and real data, including the tasks of rigid protein docking and temporal evolution of cellular differentiation processes.

A Dynamical System View of Langevin-Based Non-Convex Sampling

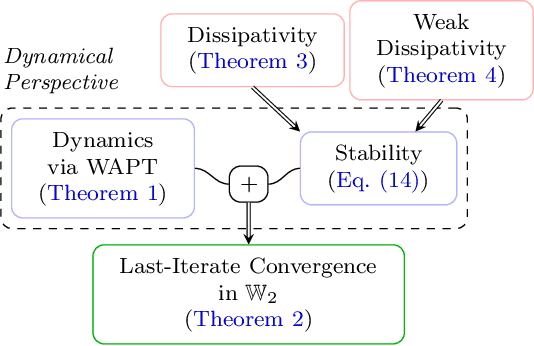
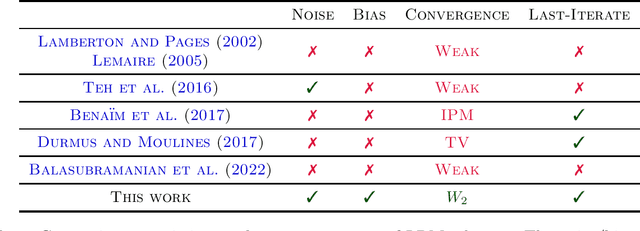
Non-convex sampling is a key challenge in machine learning, central to non-convex optimization in deep learning as well as to approximate probabilistic inference. Despite its significance, theoretically there remain many important challenges: Existing guarantees (1) typically only hold for the averaged iterates rather than the more desirable last iterates, (2) lack convergence metrics that capture the scales of the variables such as Wasserstein distances, and (3) mainly apply to elementary schemes such as stochastic gradient Langevin dynamics. In this paper, we develop a new framework that lifts the above issues by harnessing several tools from the theory of dynamical systems. Our key result is that, for a large class of state-of-the-art sampling schemes, their last-iterate convergence in Wasserstein distances can be reduced to the study of their continuous-time counterparts, which is much better understood. Coupled with standard assumptions of MCMC sampling, our theory immediately yields the last-iterate Wasserstein convergence of many advanced sampling schemes such as proximal, randomized mid-point, and Runge-Kutta integrators. Beyond existing methods, our framework also motivates more efficient schemes that enjoy the same rigorous guarantees.

Continuous-time Analysis for Variational Inequalities: An Overview and Desiderata

Algorithms that solve zero-sum games, multi-objective agent objectives, or, more generally, variational inequality (VI) problems are notoriously unstable on general problems. Owing to the increasing need for solving such problems in machine learning, this instability has been highlighted in recent years as a significant research challenge. In this paper, we provide an overview of recent progress in the use of continuous-time perspectives in the analysis and design of methods targeting the broad VI problem class. Our presentation draws parallels between single-objective problems and multi-objective problems, highlighting the challenges of the latter. We also formulate various desiderata for algorithms that apply to general VIs and we argue that achieving these desiderata may profit from an understanding of the associated continuous-time dynamics.

The Dynamics of Riemannian Robbins-Monro Algorithms

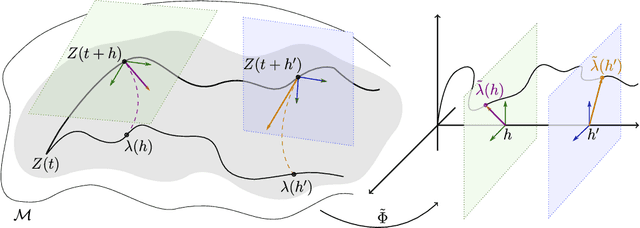
Many important learning algorithms, such as stochastic gradient methods, are often deployed to solve nonlinear problems on Riemannian manifolds. Motivated by these applications, we propose a family of Riemannian algorithms generalizing and extending the seminal stochastic approximation framework of Robbins and Monro. Compared to their Euclidean counterparts, Riemannian iterative algorithms are much less understood due to the lack of a global linear structure on the manifold. We overcome this difficulty by introducing an extended Fermi coordinate frame which allows us to map the asymptotic behavior of the proposed Riemannian Robbins-Monro (RRM) class of algorithms to that of an associated deterministic dynamical system under very mild assumptions on the underlying manifold. In so doing, we provide a general template of almost sure convergence results that mirrors and extends the existing theory for Euclidean Robbins-Monro schemes, albeit with a significantly more involved analysis that requires a number of new geometric ingredients. We showcase the flexibility of the proposed RRM framework by using it to establish the convergence of a retraction-based analogue of the popular optimistic / extra-gradient methods for solving minimization problems and games, and we provide a unified treatment for their convergence.

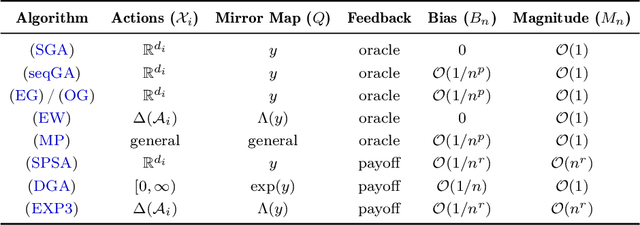
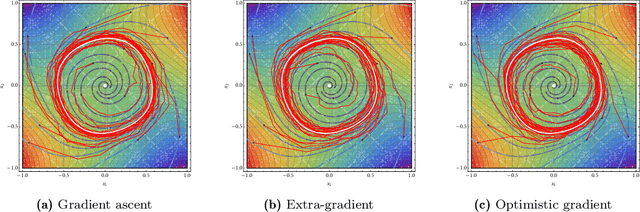
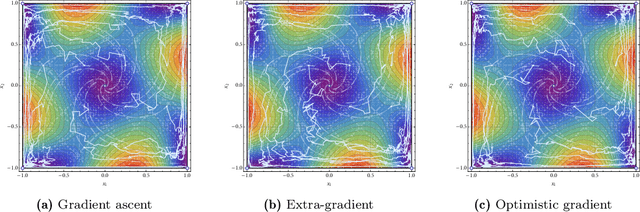
Learning in games from a stochastic approximation viewpoint

We develop a unified stochastic approximation framework for analyzing the long-run behavior of multi-agent online learning in games. Our framework is based on a "primal-dual", mirrored Robbins-Monro (MRM) template which encompasses a wide array of popular game-theoretic learning algorithms (gradient methods, their optimistic variants, the EXP3 algorithm for learning with payoff-based feedback in finite games, etc.). In addition to providing an integrated view of these algorithms, the proposed MRM blueprint allows us to obtain a broad range of new convergence results, both asymptotic and in finite time, in both continuous and finite games.

Recovering Stochastic Dynamics via Gaussian Schrödinger Bridges

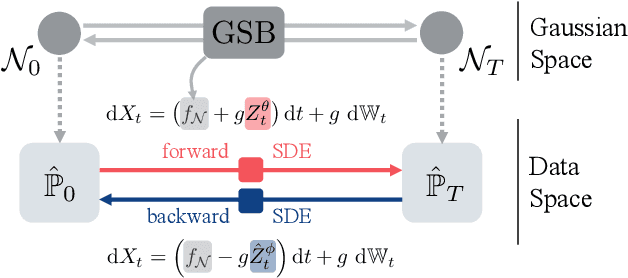
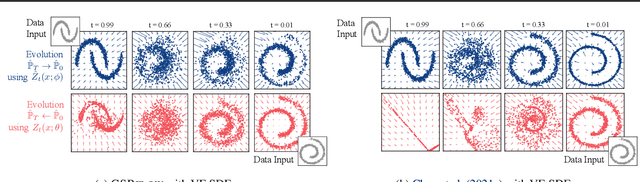
We propose a new framework to reconstruct a stochastic process $\left\{\mathbb{P}_{t}: t \in[0, T]\right\}$ using only samples from its marginal distributions, observed at start and end times $0$ and $T$. This reconstruction is useful to infer population dynamics, a crucial challenge, e.g., when modeling the time-evolution of cell populations from single-cell sequencing data. Our general framework encompasses the more specific Schr\"odinger bridge (SB) problem, where $\mathbb{P}_{t}$ represents the evolution of a thermodynamic system at almost equilibrium. Estimating such bridges is notoriously difficult, motivating our proposal for a novel adaptive scheme called the GSBflow. Our goal is to rely on Gaussian approximations of the data to provide the reference stochastic process needed to estimate SB. To that end, we solve the \acs{SB} problem with Gaussian marginals, for which we provide, as a central contribution, a closed-form solution and SDE-representation. We use these formulas to define the reference process used to estimate more complex SBs, and show that this does indeed help with its numerical solution. We obtain notable improvements when reconstructing both synthetic processes and single-cell genomics experiments.