Learning to Steer Markovian Agents under Model Uncertainty

Designing incentives for an adapting population is a ubiquitous problem in a wide array of economic applications and beyond. In this work, we study how to design additional rewards to steer multi-agent systems towards desired policies \emph{without} prior knowledge of the agents' underlying learning dynamics. We introduce a model-based non-episodic Reinforcement Learning (RL) formulation for our steering problem. Importantly, we focus on learning a \emph{history-dependent} steering strategy to handle the inherent model uncertainty about the agents' learning dynamics. We introduce a novel objective function to encode the desiderata of achieving a good steering outcome with reasonable cost. Theoretically, we identify conditions for the existence of steering strategies to guide agents to the desired policies. Complementing our theoretical contributions, we provide empirical algorithms to approximately solve our objective, which effectively tackles the challenge in learning history-dependent strategies. We demonstrate the efficacy of our algorithms through empirical evaluations.

A Hessian-Aware Stochastic Differential Equation for Modelling SGD

Continuous-time approximation of Stochastic Gradient Descent (SGD) is a crucial tool to study its escaping behaviors from stationary points. However, existing stochastic differential equation (SDE) models fail to fully capture these behaviors, even for simple quadratic objectives. Built on a novel stochastic backward error analysis framework, we derive the Hessian-Aware Stochastic Modified Equation (HA-SME), an SDE that incorporates Hessian information of the objective function into both its drift and diffusion terms. Our analysis shows that HA-SME matches the order-best approximation error guarantee among existing SDE models in the literature, while achieving a significantly reduced dependence on the smoothness parameter of the objective. Further, for quadratic objectives, under mild conditions, HA-SME is proved to be the first SDE model that recovers exactly the SGD dynamics in the distributional sense. Consequently, when the local landscape near a stationary point can be approximated by quadratics, HA-SME is expected to accurately predict the local escaping behaviors of SGD.

Share Your Representation Only: Guaranteed Improvement of the Privacy-Utility Tradeoff in Federated Learning

Repeated parameter sharing in federated learning causes significant information leakage about private data, thus defeating its main purpose: data privacy. Mitigating the risk of this information leakage, using state of the art differentially private algorithms, also does not come for free. Randomized mechanisms can prevent convergence of models on learning even the useful representation functions, especially if there is more disagreement between local models on the classification functions (due to data heterogeneity). In this paper, we consider a representation federated learning objective that encourages various parties to collaboratively refine the consensus part of the model, with differential privacy guarantees, while separately allowing sufficient freedom for local personalization (without releasing it). We prove that in the linear representation setting, while the objective is non-convex, our proposed new algorithm \DPFEDREP\ converges to a ball centered around the \emph{global optimal} solution at a linear rate, and the radius of the ball is proportional to the reciprocal of the privacy budget. With this novel utility analysis, we improve the SOTA utility-privacy trade-off for this problem by a factor of $\sqrt{d}$, where $d$ is the input dimension. We empirically evaluate our method with the image classification task on CIFAR10, CIFAR100, and EMNIST, and observe a significant performance improvement over the prior work under the same small privacy budget. The code can be found in this link: https://github.com/shenzebang/CENTAUR-Privacy-Federated-Representation-Learning.

Accelerated Doubly Stochastic Gradient Algorithm for Large-scale Empirical Risk Minimization

Nowadays, algorithms with fast convergence, small memory footprints, and low per-iteration complexity are particularly favorable for artificial intelligence applications. In this paper, we propose a doubly stochastic algorithm with a novel accelerating multi-momentum technique to solve large scale empirical risk minimization problem for learning tasks. While enjoying a provably superior convergence rate, in each iteration, such algorithm only accesses a mini batch of samples and meanwhile updates a small block of variable coordinates, which substantially reduces the amount of memory reference when both the massive sample size and ultra-high dimensionality are involved. Empirical studies on huge scale datasets are conducted to illustrate the efficiency of our method in practice.

Straggler-Resilient Personalized Federated Learning

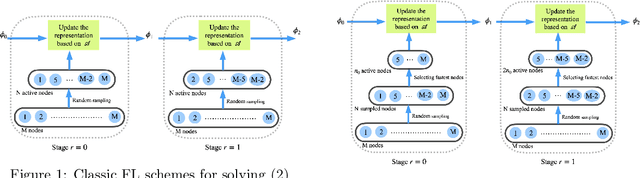
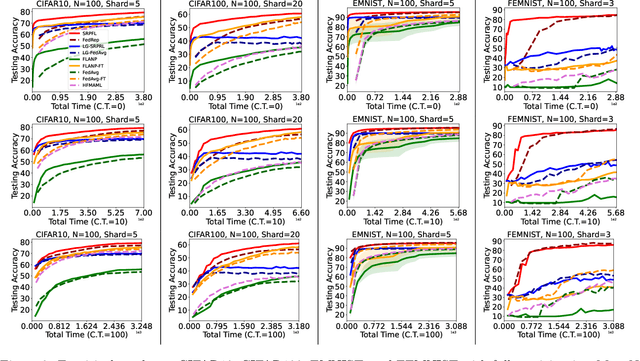
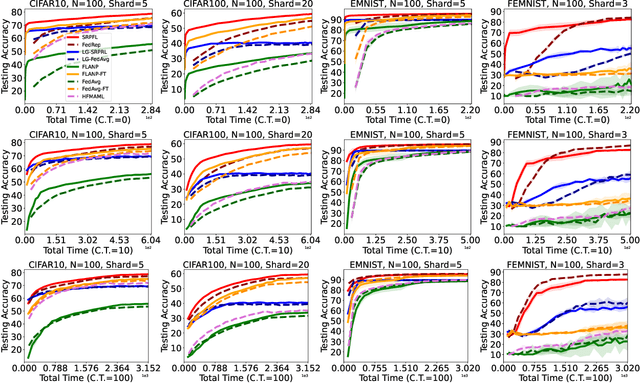
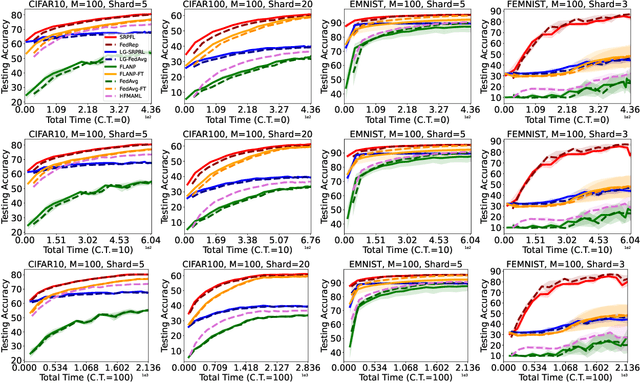
Federated Learning is an emerging learning paradigm that allows training models from samples distributed across a large network of clients while respecting privacy and communication restrictions. Despite its success, federated learning faces several challenges related to its decentralized nature. In this work, we develop a novel algorithmic procedure with theoretical speedup guarantees that simultaneously handles two of these hurdles, namely (i) data heterogeneity, i.e., data distributions can vary substantially across clients, and (ii) system heterogeneity, i.e., the computational power of the clients could differ significantly. Our method relies on ideas from representation learning theory to find a global common representation using all clients' data and learn a user-specific set of parameters leading to a personalized solution for each client. Furthermore, our method mitigates the effects of stragglers by adaptively selecting clients based on their computational characteristics and statistical significance, thus achieving, for the first time, near optimal sample complexity and provable logarithmic speedup. Experimental results support our theoretical findings showing the superiority of our method over alternative personalized federated schemes in system and data heterogeneous environments.

Self-Consistency of the Fokker-Planck Equation

The Fokker-Planck equation (FPE) is the partial differential equation that governs the density evolution of the It\^o process and is of great importance to the literature of statistical physics and machine learning. The FPE can be regarded as a continuity equation where the change of the density is completely determined by a time varying velocity field. Importantly, this velocity field also depends on the current density function. As a result, the ground-truth velocity field can be shown to be the solution of a fixed-point equation, a property that we call self-consistency. In this paper, we exploit this concept to design a potential function of the hypothesis velocity fields, and prove that, if such a function diminishes to zero during the training procedure, the trajectory of the densities generated by the hypothesis velocity fields converges to the solution of the FPE in the Wasserstein-2 sense. The proposed potential function is amenable to neural-network based parameterization as the stochastic gradient with respect to the parameter can be efficiently computed. Once a parameterized model, such as Neural Ordinary Differential Equation is trained, we can generate the entire trajectory to the FPE.

A Federated Learning Framework for Nonconvex-PL Minimax Problems

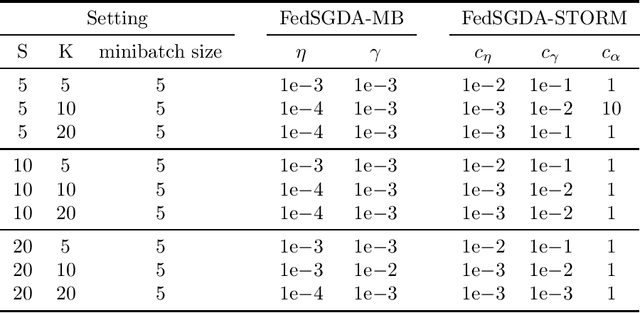
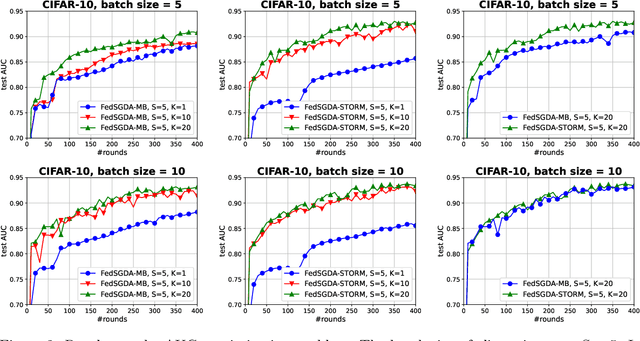
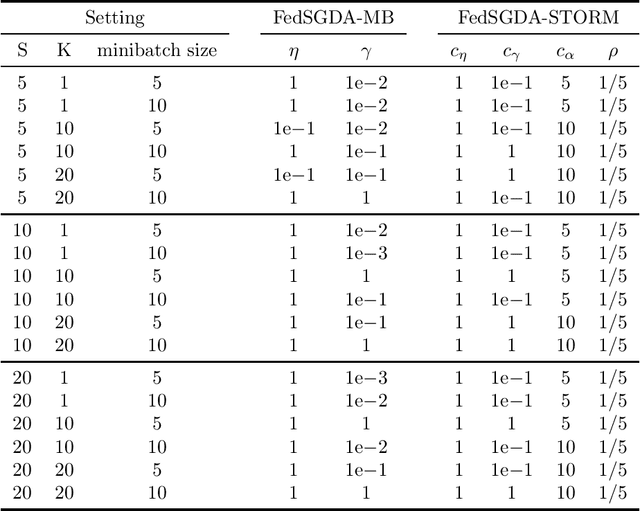
We consider a general class of nonconvex-PL minimax problems in the cross-device federated learning setting. Although nonconvex-PL minimax problems have received a lot of interest in recent years, existing algorithms do not apply to the cross-device federated learning setting which is substantially different from conventional distributed settings and poses new challenges. To bridge this gap, we propose an algorithmic framework named FedSGDA. FedSGDA performs multiple local update steps on a subset of active clients in each round and leverages global gradient estimates to correct the bias in local update directions. By incorporating FedSGDA with two representative global gradient estimators, we obtain two specific algorithms. We establish convergence rates of the proposed algorithms by using novel potential functions. Experimental results on synthetic and real data corroborate our theory and demonstrate the effectiveness of our algorithms.

Federated Functional Gradient Boosting

In this paper, we initiate a study of functional minimization in Federated Learning. First, in the semi-heterogeneous setting, when the marginal distributions of the feature vectors on client machines are identical, we develop the federated functional gradient boosting (FFGB) method that provably converges to the global minimum. Subsequently, we extend our results to the fully-heterogeneous setting (where marginal distributions of feature vectors may differ) by designing an efficient variant of FFGB called FFGB.C, with provable convergence to a neighborhood of the global minimum within a radius that depends on the total variation distances between the client feature distributions. For the special case of square loss, but still in the fully heterogeneous setting, we design the FFGB.L method that also enjoys provable convergence to a neighborhood of the global minimum but within a radius depending on the much tighter Wasserstein-1 distances. For both FFGB.C and FFGB.L, the radii of convergence shrink to zero as the feature distributions become more homogeneous. Finally, we conduct proof-of-concept experiments to demonstrate the benefits of our approach against natural baselines.

Partial Gromov-Wasserstein Learning for Partial Graph Matching

Graph matching finds the correspondence of nodes across two graphs and is a basic task in graph-based machine learning. Numerous existing methods match every node in one graph to one node in the other graph whereas two graphs usually overlap partially in many \realworld{} applications. In this paper, a partial Gromov-Wasserstein learning framework is proposed for partially matching two graphs, which fuses the partial Gromov-Wasserstein distance and the partial Wasserstein distance as the objective and updates the partial transport map and the node embedding in an alternating fashion. The proposed framework transports a fraction of the probability mass and matches node pairs with high relative similarities across the two graphs. Incorporating an embedding learning method, heterogeneous graphs can also be matched. Numerical experiments on both synthetic and \realworld{} graphs demonstrate that our framework can improve the F1 score by at least $20\%$ and often much more.

Sinkhorn Natural Gradient for Generative Models

We consider the problem of minimizing a functional over a parametric family of probability measures, where the parameterization is characterized via a push-forward structure. An important application of this problem is in training generative adversarial networks. In this regard, we propose a novel Sinkhorn Natural Gradient (SiNG) algorithm which acts as a steepest descent method on the probability space endowed with the Sinkhorn divergence. We show that the Sinkhorn information matrix (SIM), a key component of SiNG, has an explicit expression and can be evaluated accurately in complexity that scales logarithmically with respect to the desired accuracy. This is in sharp contrast to existing natural gradient methods that can only be carried out approximately. Moreover, in practical applications when only Monte-Carlo type integration is available, we design an empirical estimator for SIM and provide the stability analysis. In our experiments, we quantitatively compare SiNG with state-of-the-art SGD-type solvers on generative tasks to demonstrate its efficiency and efficacy of our method.