Improved Complexity for Smooth Nonconvex Optimization: A Two-Level Online Learning Approach with Quasi-Newton Methods

We study the problem of finding an $\epsilon$-first-order stationary point (FOSP) of a smooth function, given access only to gradient information. The best-known gradient query complexity for this task, assuming both the gradient and Hessian of the objective function are Lipschitz continuous, is ${O}(\epsilon^{-7/4})$. In this work, we propose a method with a gradient complexity of ${O}(d^{1/4}\epsilon^{-13/8})$, where $d$ is the problem dimension, leading to an improved complexity when $d = {O}(\epsilon^{-1/2})$. To achieve this result, we design an optimization algorithm that, underneath, involves solving two online learning problems. Specifically, we first reformulate the task of finding a stationary point for a nonconvex problem as minimizing the regret in an online convex optimization problem, where the loss is determined by the gradient of the objective function. Then, we introduce a novel optimistic quasi-Newton method to solve this online learning problem, with the Hessian approximation update itself framed as an online learning problem in the space of matrices. Beyond improving the complexity bound for achieving an $\epsilon$-FOSP using a gradient oracle, our result provides the first guarantee suggesting that quasi-Newton methods can potentially outperform gradient descent-type methods in nonconvex settings.

Learning Mixtures of Experts with EM

Mixtures of Experts (MoE) are Machine Learning models that involve partitioning the input space, with a separate "expert" model trained on each partition. Recently, MoE have become popular as components in today's large language models as a means to reduce training and inference costs. There, the partitioning function and the experts are both learnt jointly via gradient descent on the log-likelihood. In this paper we focus on studying the efficiency of the Expectation Maximization (EM) algorithm for the training of MoE models. We first rigorously analyze EM for the cases of linear or logistic experts, where we show that EM is equivalent to Mirror Descent with unit step size and a Kullback-Leibler Divergence regularizer. This perspective allows us to derive new convergence results and identify conditions for local linear convergence based on the signal-to-noise ratio (SNR). Experiments on synthetic and (small-scale) real-world data show that EM outperforms the gradient descent algorithm both in terms of convergence rate and the achieved accuracy.

Meta-Learning Adaptable Foundation Models

The power of foundation models (FMs) lies in their capacity to learn highly expressive representations that can be adapted to a broad spectrum of tasks. However, these pretrained models require multiple stages of fine-tuning to become effective for downstream applications. Conventionally, the model is first retrained on the aggregate of a diverse set of tasks of interest and then adapted to specific low-resource downstream tasks by utilizing a parameter-efficient fine-tuning (PEFT) scheme. While this two-phase procedure seems reasonable, the independence of the retraining and fine-tuning phases causes a major issue, as there is no guarantee the retrained model will achieve good performance post-fine-tuning. To explicitly address this issue, we introduce a meta-learning framework infused with PEFT in this intermediate retraining stage to learn a model that can be easily adapted to unseen tasks. For our theoretical results, we focus on linear models using low-rank adaptations. In this setting, we demonstrate the suboptimality of standard retraining for finding an adaptable set of parameters. Further, we prove that our method recovers the optimally adaptable parameters. We then apply these theoretical insights to retraining the RoBERTa model to predict the continuation of conversations between different personas within the ConvAI2 dataset. Empirically, we observe significant performance benefits using our proposed meta-learning scheme during retraining relative to the conventional approach.

On the Crucial Role of Initialization for Matrix Factorization

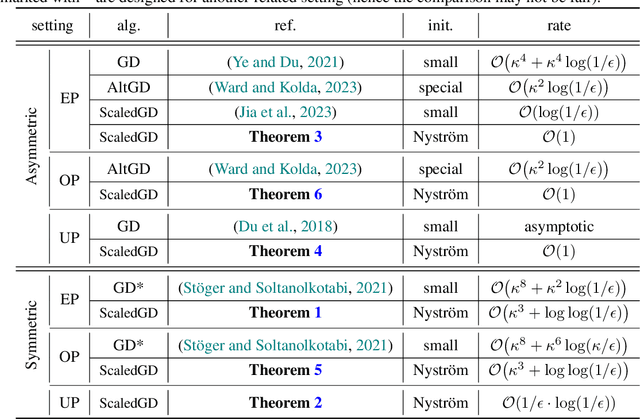
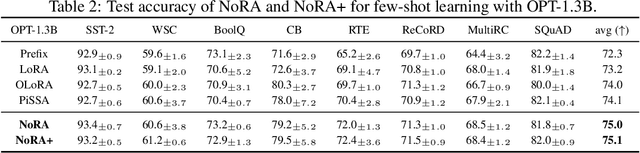
This work revisits the classical low-rank matrix factorization problem and unveils the critical role of initialization in shaping convergence rates for such nonconvex and nonsmooth optimization. We introduce Nystrom initialization, which significantly improves the global convergence of Scaled Gradient Descent (ScaledGD) in both symmetric and asymmetric matrix factorization tasks. Specifically, we prove that ScaledGD with Nystrom initialization achieves quadratic convergence in cases where only linear rates were previously known. Furthermore, we extend this initialization to low-rank adapters (LoRA) commonly used for finetuning foundation models. Our approach, NoRA, i.e., LoRA with Nystrom initialization, demonstrates superior performance across various downstream tasks and model scales, from 1B to 7B parameters, in large language and diffusion models.

Online Learning Guided Quasi-Newton Methods with Global Non-Asymptotic Convergence

In this paper, we propose a quasi-Newton method for solving smooth and monotone nonlinear equations, including unconstrained minimization and minimax optimization as special cases. For the strongly monotone setting, we establish two global convergence bounds: (i) a linear convergence rate that matches the rate of the celebrated extragradient method, and (ii) an explicit global superlinear convergence rate that provably surpasses the linear convergence rate after at most ${O}(d)$ iterations, where $d$ is the problem's dimension. In addition, for the case where the operator is only monotone, we prove a global convergence rate of ${O}(\min\{{1}/{k},{\sqrt{d}}/{k^{1.25}}\})$ in terms of the duality gap. This matches the rate of the extragradient method when $k = {O}(d^2)$ and is faster when $k = \Omega(d^2)$. These results are the first global convergence results to demonstrate a provable advantage of a quasi-Newton method over the extragradient method, without querying the Jacobian of the operator. Unlike classical quasi-Newton methods, we achieve this by using the hybrid proximal extragradient framework and a novel online learning approach for updating the Jacobian approximation matrices. Specifically, guided by the convergence analysis, we formulate the Jacobian approximation update as an online convex optimization problem over non-symmetric matrices, relating the regret of the online problem to the convergence rate of our method. To facilitate efficient implementation, we further develop a tailored online learning algorithm based on an approximate separation oracle, which preserves structures such as symmetry and sparsity in the Jacobian matrices.

Convergence Analysis of Adaptive Gradient Methods under Refined Smoothness and Noise Assumptions

Adaptive gradient methods are arguably the most successful optimization algorithms for neural network training. While it is well-known that adaptive gradient methods can achieve better dimensional dependence than stochastic gradient descent (SGD) under favorable geometry for stochastic convex optimization, the theoretical justification for their success in stochastic non-convex optimization remains elusive. In this paper, we aim to close this gap by analyzing the convergence rates of AdaGrad measured by the $\ell_1$-norm of the gradient. Specifically, when the objective has $L$-Lipschitz gradient and the stochastic gradient variance is bounded by $\sigma^2$, we prove a worst-case convergence rate of $\tilde{\mathcal{O}}(\frac{\sqrt{d}L}{\sqrt{T}} + \frac{\sqrt{d} \sigma}{T^{1/4}})$, where $d$ is the dimension of the problem.We also present a lower bound of ${\Omega}(\frac{\sqrt{d}}{\sqrt{T}})$ for minimizing the gradient $\ell_1$-norm in the deterministic setting, showing the tightness of our upper bound in the noiseless case. Moreover, under more fine-grained assumptions on the smoothness structure of the objective and the gradient noise and under favorable gradient $\ell_1/\ell_2$ geometry, we show that AdaGrad can potentially shave a factor of $\sqrt{d}$ compared to SGD. To the best of our knowledge, this is the first result for adaptive gradient methods that demonstrates a provable gain over SGD in the non-convex setting.

Adaptive and Optimal Second-order Optimistic Methods for Minimax Optimization

We propose adaptive, line search-free second-order methods with optimal rate of convergence for solving convex-concave min-max problems. By means of an adaptive step size, our algorithms feature a simple update rule that requires solving only one linear system per iteration, eliminating the need for line search or backtracking mechanisms. Specifically, we base our algorithms on the optimistic method and appropriately combine it with second-order information. Moreover, distinct from common adaptive schemes, we define the step size recursively as a function of the gradient norm and the prediction error in the optimistic update. We first analyze a variant where the step size requires knowledge of the Lipschitz constant of the Hessian. Under the additional assumption of Lipschitz continuous gradients, we further design a parameter-free version by tracking the Hessian Lipschitz constant locally and ensuring the iterates remain bounded. We also evaluate the practical performance of our algorithm by comparing it to existing second-order algorithms for minimax optimization.

Stochastic Newton Proximal Extragradient Method

Stochastic second-order methods achieve fast local convergence in strongly convex optimization by using noisy Hessian estimates to precondition the gradient. However, these methods typically reach superlinear convergence only when the stochastic Hessian noise diminishes, increasing per-iteration costs over time. Recent work in [arXiv:2204.09266] addressed this with a Hessian averaging scheme that achieves superlinear convergence without higher per-iteration costs. Nonetheless, the method has slow global convergence, requiring up to $\tilde{O}(\kappa^2)$ iterations to reach the superlinear rate of $\tilde{O}((1/t)^{t/2})$, where $\kappa$ is the problem's condition number. In this paper, we propose a novel stochastic Newton proximal extragradient method that improves these bounds, achieving a faster global linear rate and reaching the same fast superlinear rate in $\tilde{O}(\kappa)$ iterations. We accomplish this by extending the Hybrid Proximal Extragradient (HPE) framework, achieving fast global and local convergence rates for strongly convex functions with access to a noisy Hessian oracle.

In-Context Learning with Transformers: Softmax Attention Adapts to Function Lipschitzness

A striking property of transformers is their ability to perform in-context learning (ICL), a machine learning framework in which the learner is presented with a novel context during inference implicitly through some data, and tasked with making a prediction in that context. As such that learner must adapt to the context without additional training. We explore the role of softmax attention in an ICL setting where each context encodes a regression task. We show that an attention unit learns a window that it uses to implement a nearest-neighbors predictor adapted to the landscape of the pretraining tasks. Specifically, we show that this window widens with decreasing Lipschitzness and increasing label noise in the pretraining tasks. We also show that on low-rank, linear problems, the attention unit learns to project onto the appropriate subspace before inference. Further, we show that this adaptivity relies crucially on the softmax activation and thus cannot be replicated by the linear activation often studied in prior theoretical analyses.

An Accelerated Gradient Method for Simple Bilevel Optimization with Convex Lower-level Problem

In this paper, we focus on simple bilevel optimization problems, where we minimize a convex smooth objective function over the optimal solution set of another convex smooth constrained optimization problem. We present a novel bilevel optimization method that locally approximates the solution set of the lower-level problem using a cutting plane approach and employs an accelerated gradient-based update to reduce the upper-level objective function over the approximated solution set. We measure the performance of our method in terms of suboptimality and infeasibility errors and provide non-asymptotic convergence guarantees for both error criteria. Specifically, when the feasible set is compact, we show that our method requires at most $\mathcal{O}(\max\{1/\sqrt{\epsilon_{f}}, 1/\epsilon_g\})$ iterations to find a solution that is $\epsilon_f$-suboptimal and $\epsilon_g$-infeasible. Moreover, under the additional assumption that the lower-level objective satisfies the $r$-th H\"olderian error bound, we show that our method achieves an iteration complexity of $\mathcal{O}(\max\{\epsilon_{f}^{-\frac{2r-1}{2r}},\epsilon_{g}^{-\frac{2r-1}{2r}}\})$, which matches the optimal complexity of single-level convex constrained optimization when $r=1$.