In-Context Learning with Transformers: Softmax Attention Adapts to Function Lipschitzness

A striking property of transformers is their ability to perform in-context learning (ICL), a machine learning framework in which the learner is presented with a novel context during inference implicitly through some data, and tasked with making a prediction in that context. As such that learner must adapt to the context without additional training. We explore the role of softmax attention in an ICL setting where each context encodes a regression task. We show that an attention unit learns a window that it uses to implement a nearest-neighbors predictor adapted to the landscape of the pretraining tasks. Specifically, we show that this window widens with decreasing Lipschitzness and increasing label noise in the pretraining tasks. We also show that on low-rank, linear problems, the attention unit learns to project onto the appropriate subspace before inference. Further, we show that this adaptivity relies crucially on the softmax activation and thus cannot be replicated by the linear activation often studied in prior theoretical analyses.

InfoNCE Loss Provably Learns Cluster-Preserving Representations

The goal of contrasting learning is to learn a representation that preserves underlying clusters by keeping samples with similar content, e.g. the ``dogness'' of a dog, close to each other in the space generated by the representation. A common and successful approach for tackling this unsupervised learning problem is minimizing the InfoNCE loss associated with the training samples, where each sample is associated with their augmentations (positive samples such as rotation, crop) and a batch of negative samples (unrelated samples). To the best of our knowledge, it was unanswered if the representation learned by minimizing the InfoNCE loss preserves the underlying data clusters, as it only promotes learning a representation that is faithful to augmentations, i.e., an image and its augmentations have the same representation. Our main result is to show that the representation learned by InfoNCE with a finite number of negative samples is also consistent with respect to clusters in the data, under the condition that the augmentation sets within clusters may be non-overlapping but are close and intertwined, relative to the complexity of the learning function class.

A Theoretical Justification for Image Inpainting using Denoising Diffusion Probabilistic Models

We provide a theoretical justification for sample recovery using diffusion based image inpainting in a linear model setting. While most inpainting algorithms require retraining with each new mask, we prove that diffusion based inpainting generalizes well to unseen masks without retraining. We analyze a recently proposed popular diffusion based inpainting algorithm called RePaint (Lugmayr et al., 2022), and show that it has a bias due to misalignment that hampers sample recovery even in a two-state diffusion process. Motivated by our analysis, we propose a modified RePaint algorithm we call RePaint$^+$ that provably recovers the underlying true sample and enjoys a linear rate of convergence. It achieves this by rectifying the misalignment error present in drift and dispersion of the reverse process. To the best of our knowledge, this is the first linear convergence result for a diffusion based image inpainting algorithm.

PAC Generalization via Invariant Representations

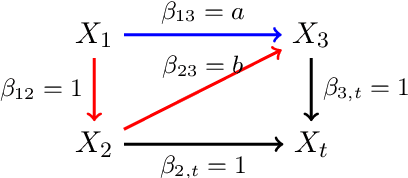
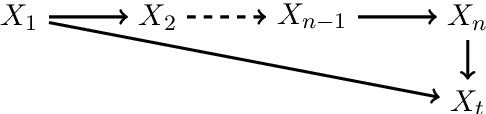
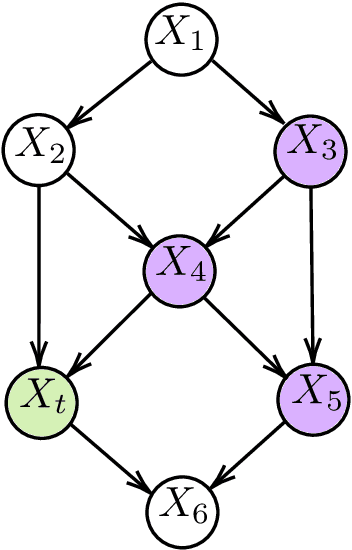
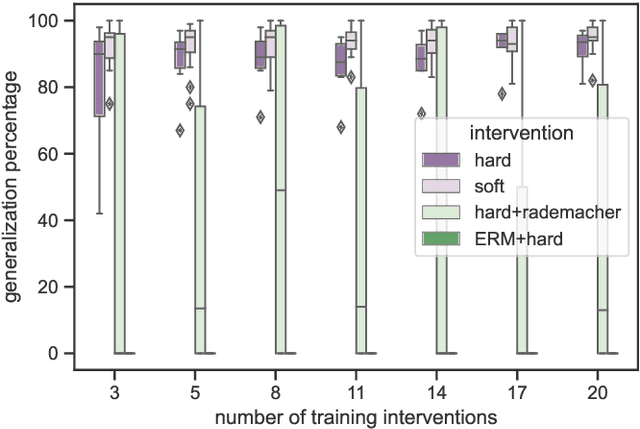
One method for obtaining generalizable solutions to machine learning tasks when presented with diverse training environments is to find invariant representations of the data. These are representations of the covariates such that the best model on top of the representation is invariant across training environments. In the context of linear Structural Equation Models (SEMs), invariant representations might allow us to learn models with out-of-distribution guarantees, i.e., models that are robust to interventions in the SEM. To address the invariant representation problem in a finite sample setting, we consider the notion of $\epsilon$-approximate invariance. We study the following question: If a representation is approximately invariant with respect to a given number of training interventions, will it continue to be approximately invariant on a larger collection of unseen SEMs? This larger collection of SEMs is generated through a parameterized family of interventions. Inspired by PAC learning, we obtain finite-sample out-of-distribution generalization guarantees for approximate invariance that holds probabilistically over a family of linear SEMs without faithfulness assumptions. Our results show bounds that do not scale in ambient dimension when intervention sites are restricted to lie in a constant size subset of in-degree bounded nodes. We also show how to extend our results to a linear indirect observation model that incorporates latent variables.

Improved Algorithms for Misspecified Linear Markov Decision Processes

For the misspecified linear Markov decision process (MLMDP) model of Jin et al. [2020], we propose an algorithm with three desirable properties. (P1) Its regret after $K$ episodes scales as $K \max \{ \varepsilon_{\text{mis}}, \varepsilon_{\text{tol}} \}$, where $\varepsilon_{\text{mis}}$ is the degree of misspecification and $\varepsilon_{\text{tol}}$ is a user-specified error tolerance. (P2) Its space and per-episode time complexities remain bounded as $K \rightarrow \infty$. (P3) It does not require $\varepsilon_{\text{mis}}$ as input. To our knowledge, this is the first algorithm satisfying all three properties. For concrete choices of $\varepsilon_{\text{tol}}$, we also improve existing regret bounds (up to log factors) while achieving either (P2) or (P3) (existing algorithms satisfy neither). At a high level, our algorithm generalizes (to MLMDPs) and refines the Sup-Lin-UCB algorithm, which Takemura et al. [2021] recently showed satisfies (P3) in the contextual bandit setting.

L1 Regression with Lewis Weights Subsampling

We consider the problem of finding an approximate solution to $\ell_1$ regression while only observing a small number of labels. Given an $n \times d$ unlabeled data matrix $X$, we must choose a small set of $m \ll n$ rows to observe the labels of, then output an estimate $\widehat{\beta}$ whose error on the original problem is within a $1 + \varepsilon$ factor of optimal. We show that sampling from $X$ according to its Lewis weights and outputting the empirical minimizer succeeds with probability $1-\delta$ for $m > O(\frac{1}{\varepsilon^2} d \log \frac{d}{\varepsilon \delta})$. This is analogous to the performance of sampling according to leverage scores for $\ell_2$ regression, but with exponentially better dependence on $\delta$. We also give a corresponding lower bound of $\Omega(\frac{d}{\varepsilon^2} + (d + \frac{1}{\varepsilon^2}) \log\frac{1}{\delta})$.

Regret Bounds for Stochastic Shortest Path Problems with Linear Function Approximation

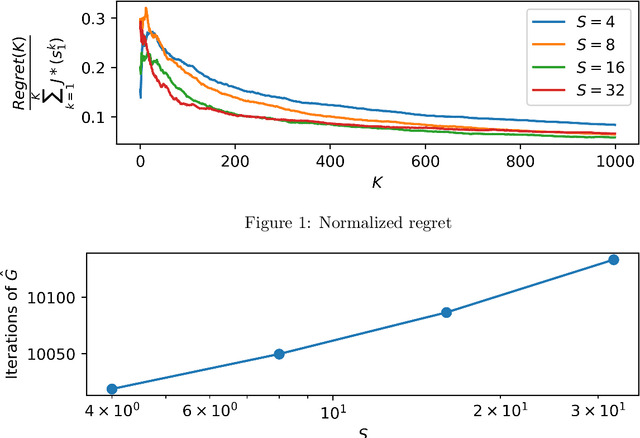
We propose two algorithms for episodic stochastic shortest path problems with linear function approximation. The first is computationally expensive but provably obtains $\tilde{O} (\sqrt{B_\star^3 d^3 K/c_{min}} )$ regret, where $B_\star$ is a (known) upper bound on the optimal cost-to-go function, $d$ is the feature dimension, $K$ is the number of episodes, and $c_{min}$ is the minimal cost of non-goal state-action pairs (assumed to be positive). The second is computationally efficient in practice, and we conjecture that it obtains the same regret bound. Both algorithms are based on an optimistic least-squares version of value iteration analogous to the finite-horizon backward induction approach from Jin et al. 2020. To the best of our knowledge, these are the first regret bounds for stochastic shortest path that are independent of the size of the state and action spaces.

Stochastic Linear Bandits with Protected Subspace

We study a variant of the stochastic linear bandit problem wherein we optimize a linear objective function but rewards are accrued only orthogonal to an unknown subspace (which we interpret as a \textit{protected space}) given only zero-order stochastic oracle access to both the objective itself and protected subspace. In particular, at each round, the learner must choose whether to query the objective or the protected subspace alongside choosing an action. Our algorithm, derived from the OFUL principle, uses some of the queries to get an estimate of the protected space, and (in almost all rounds) plays optimistically with respect to a confidence set for this space. We provide a $\tilde{O}(sd\sqrt{T})$ regret upper bound in the case where the action space is the complete unit ball in $\mathbb{R}^d$, $s < d$ is the dimension of the protected subspace, and $T$ is the time horizon. Moreover, we demonstrate that a discrete action space can lead to linear regret with an optimistic algorithm, reinforcing the sub-optimality of optimism in certain settings. We also show that protection constraints imply that for certain settings, no consistent algorithm can have a regret smaller than $\Omega(T^{3/4}).$ We finally empirically validate our results with synthetic and real datasets.