Context-Free Synthetic Data Mitigates Forgetting

Fine-tuning a language model often results in a degradation of its existing performance on other tasks, due to a shift in the model parameters; this phenomenon is often referred to as (catastrophic) forgetting. We are interested in mitigating this, in settings where we only have access to the model weights but no access to its training data/recipe. A natural approach is to penalize the KL divergence between the original model and the new one. Our main realization is that a simple process - which we term context-free generation - allows for an approximate unbiased estimation of this KL divergence. We show that augmenting a fine-tuning dataset with context-free generations mitigates forgetting, in two settings: (a) preserving the zero-shot performance of pretrained-only models, and (b) preserving the reasoning performance of thinking models. We show that contextual synthetic data, and even a portion of the pretraining data, are less effective. We also investigate the effect of choices like generation temperature, data ratios etc. We present our results for OLMo-1B for pretrained-only setting and R1-Distill-Llama-8B for the reasoning setting.

Asymptotically-Optimal Gaussian Bandits with Side Observations

We study the problem of Gaussian bandits with general side information, as first introduced by Wu, Szepesvari, and Gyorgy. In this setting, the play of an arm reveals information about other arms, according to an arbitrary a priori known side information matrix: each element of this matrix encodes the fidelity of the information that the ``row'' arm reveals about the ``column'' arm. In the case of Gaussian noise, this model subsumes standard bandits, full-feedback, and graph-structured feedback as special cases. In this work, we first construct an LP-based asymptotic instance-dependent lower bound on the regret. The LP optimizes the cost (regret) required to reliably estimate the suboptimality gap of each arm. This LP lower bound motivates our main contribution: the first known asymptotically optimal algorithm for this general setting.

InfoPO: On Mutual Information Maximization for Large Language Model Alignment

We study the post-training of large language models (LLMs) with human preference data. Recently, direct preference optimization and its variants have shown considerable promise in aligning language models, eliminating the need for reward models and online sampling. Despite these benefits, these methods rely on explicit assumptions about the Bradley-Terry (BT) model, which makes them prone to overfitting and results in suboptimal performance, particularly on reasoning-heavy tasks. To address these challenges, we propose a principled preference fine-tuning algorithm called InfoPO, which effectively and efficiently aligns large language models using preference data. InfoPO eliminates the reliance on the BT model and prevents the likelihood of the chosen response from decreasing. Extensive experiments confirm that InfoPO consistently outperforms established baselines on widely used open benchmarks, particularly in reasoning tasks.

Geometric Median Matching for Robust k-Subset Selection from Noisy Data

Data pruning -- the combinatorial task of selecting a small and representative subset from a large dataset, is crucial for mitigating the enormous computational costs associated with training data-hungry modern deep learning models at scale. Since large scale data collections are invariably noisy, developing data pruning strategies that remain robust even in the presence of corruption is critical in practice. However, existing data pruning methods often fail under high corruption rates due to their reliance on empirical mean estimation, which is highly sensitive to outliers. In response, we propose Geometric Median (GM) Matching, a novel k-subset selection strategy that leverages Geometric Median -- a robust estimator with an optimal breakdown point of 1/2; to enhance resilience against noisy data. Our method iteratively selects a k-subset such that the mean of the subset approximates the GM of the (potentially) noisy dataset, ensuring robustness even under arbitrary corruption. We provide theoretical guarantees, showing that GM Matching enjoys an improved O(1/k) convergence rate -- a quadratic improvement over random sampling, even under arbitrary corruption. Extensive experiments across image classification and image generation tasks demonstrate that GM Matching consistently outperforms existing pruning approaches, particularly in high-corruption settings and at high pruning rates; making it a strong baseline for robust data pruning.

Upweighting Easy Samples in Fine-Tuning Mitigates Forgetting

Fine-tuning a pre-trained model on a downstream task often degrades its original capabilities, a phenomenon known as "catastrophic forgetting". This is especially an issue when one does not have access to the data and recipe used to develop the pre-trained model. Under this constraint, most existing methods for mitigating forgetting are inapplicable. To address this challenge, we propose a sample weighting scheme for the fine-tuning data solely based on the pre-trained model's losses. Specifically, we upweight the easy samples on which the pre-trained model's loss is low and vice versa to limit the drift from the pre-trained model. Our approach is orthogonal and yet complementary to existing methods; while such methods mostly operate on parameter or gradient space, we concentrate on the sample space. We theoretically analyze the impact of fine-tuning with our method in a linear setting, showing that it stalls learning in a certain subspace which inhibits overfitting to the target task. We empirically demonstrate the efficacy of our method on both language and vision tasks. As an example, when fine-tuning Gemma 2 2B on MetaMathQA, our method results in only a $0.8\%$ drop in accuracy on GSM8K (another math dataset) compared to standard fine-tuning, while preserving $5.4\%$ more accuracy on the pre-training datasets. Our code is publicly available at https://github.com/sanyalsunny111/FLOW_finetuning .

Learning Mixtures of Experts with EM

Mixtures of Experts (MoE) are Machine Learning models that involve partitioning the input space, with a separate "expert" model trained on each partition. Recently, MoE have become popular as components in today's large language models as a means to reduce training and inference costs. There, the partitioning function and the experts are both learnt jointly via gradient descent on the log-likelihood. In this paper we focus on studying the efficiency of the Expectation Maximization (EM) algorithm for the training of MoE models. We first rigorously analyze EM for the cases of linear or logistic experts, where we show that EM is equivalent to Mirror Descent with unit step size and a Kullback-Leibler Divergence regularizer. This perspective allows us to derive new convergence results and identify conditions for local linear convergence based on the signal-to-noise ratio (SNR). Experiments on synthetic and (small-scale) real-world data show that EM outperforms the gradient descent algorithm both in terms of convergence rate and the achieved accuracy.

RARe: Retrieval Augmented Retrieval with In-Context Examples

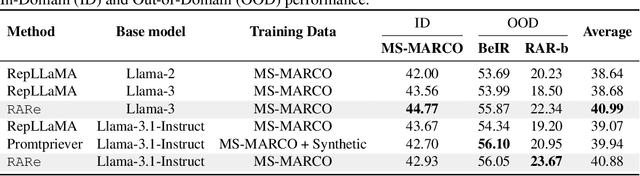
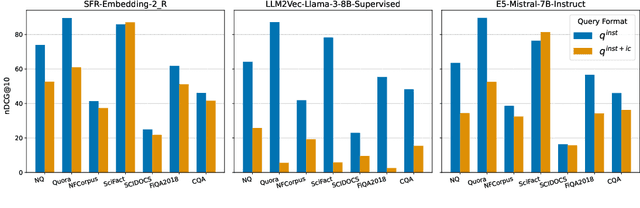
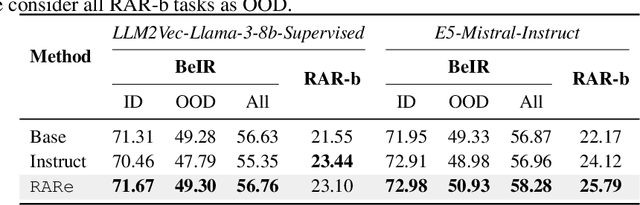
We investigate whether in-context examples, widely used in decoder-only language models (LLMs), can improve embedding model performance in retrieval tasks. Unlike in LLMs, naively prepending in-context examples (query-document pairs) to the target query at inference time does not work out of the box. We introduce a simple approach to enable retrievers to use in-context examples. Our approach, RARe, finetunes a pre-trained model with in-context examples whose query is semantically similar to the target query. This can be applied to adapt various base architectures (i.e., decoder-only language models, retriever models) and consistently achieves performance gains of up to +2.72% nDCG across various open-domain retrieval datasets (BeIR, RAR-b). In particular, we find RARe exhibits stronger out-of-domain generalization compared to models using queries without in-context examples, similar to what is seen for in-context learning in LLMs. We further provide analysis on the design choices of in-context example augmentation and lay the foundation for future work in this space.

Geometric Median (GM) Matching for Robust Data Pruning

Data pruning, the combinatorial task of selecting a small and informative subset from a large dataset, is crucial for mitigating the enormous computational costs associated with training data-hungry modern deep learning models at scale. Since large-scale data collections are invariably noisy, developing data pruning strategies that remain robust even in the presence of corruption is critical in practice. Unfortunately, the existing heuristics for (robust) data pruning lack theoretical coherence and rely on heroic assumptions, that are, often unattainable, by the very nature of the problem setting. Moreover, these strategies often yield sub-optimal neural scaling laws even compared to random sampling, especially in scenarios involving strong corruption and aggressive pruning rates -- making provably robust data pruning an open challenge. In response, in this work, we propose Geometric Median ($\gm$) Matching -- a herding~\citep{welling2009herding} style greedy algorithm -- that yields a $k$-subset such that the mean of the subset approximates the geometric median of the (potentially) noisy dataset. Theoretically, we show that $\gm$ Matching enjoys an improved $\gO(1/k)$ scaling over $\gO(1/\sqrt{k})$ scaling of uniform sampling; while achieving the optimal breakdown point of 1/2 even under arbitrary corruption. Extensive experiments across popular deep learning benchmarks indicate that $\gm$ Matching consistently outperforms prior state-of-the-art; the gains become more profound at high rates of corruption and aggressive pruning rates; making $\gm$ Matching a strong baseline for future research in robust data pruning.

DataComp-LM: In search of the next generation of training sets for language models

We introduce DataComp for Language Models (DCLM), a testbed for controlled dataset experiments with the goal of improving language models. As part of DCLM, we provide a standardized corpus of 240T tokens extracted from Common Crawl, effective pretraining recipes based on the OpenLM framework, and a broad suite of 53 downstream evaluations. Participants in the DCLM benchmark can experiment with data curation strategies such as deduplication, filtering, and data mixing at model scales ranging from 412M to 7B parameters. As a baseline for DCLM, we conduct extensive experiments and find that model-based filtering is key to assembling a high-quality training set. The resulting dataset, DCLM-Baseline enables training a 7B parameter language model from scratch to 64% 5-shot accuracy on MMLU with 2.6T training tokens. Compared to MAP-Neo, the previous state-of-the-art in open-data language models, DCLM-Baseline represents a 6.6 percentage point improvement on MMLU while being trained with 40% less compute. Our baseline model is also comparable to Mistral-7B-v0.3 and Llama 3 8B on MMLU (63% & 66%), and performs similarly on an average of 53 natural language understanding tasks while being trained with 6.6x less compute than Llama 3 8B. Our results highlight the importance of dataset design for training language models and offer a starting point for further research on data curation.

Retraining with Predicted Hard Labels Provably Increases Model Accuracy

The performance of a model trained with \textit{noisy labels} is often improved by simply \textit{retraining} the model with its own predicted \textit{hard} labels (i.e., $1$/$0$ labels). Yet, a detailed theoretical characterization of this phenomenon is lacking. In this paper, we theoretically analyze retraining in a linearly separable setting with randomly corrupted labels given to us and prove that retraining can improve the population accuracy obtained by initially training with the given (noisy) labels. To the best of our knowledge, this is the first such theoretical result. Retraining finds application in improving training with label differential privacy (DP) which involves training with noisy labels. We empirically show that retraining selectively on the samples for which the predicted label matches the given label significantly improves label DP training at \textit{no extra privacy cost}; we call this \textit{consensus-based retraining}. For e.g., when training ResNet-18 on CIFAR-100 with $\epsilon=3$ label DP, we obtain $6.4\%$ improvement in accuracy with consensus-based retraining.