Logarithmic Bayes Regret Bounds

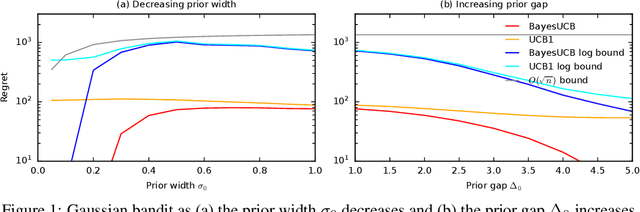
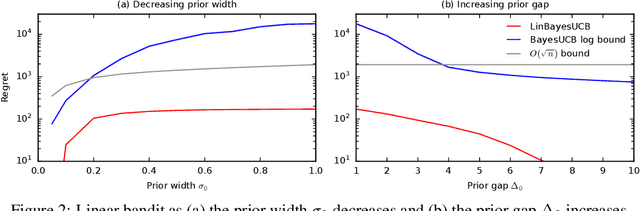
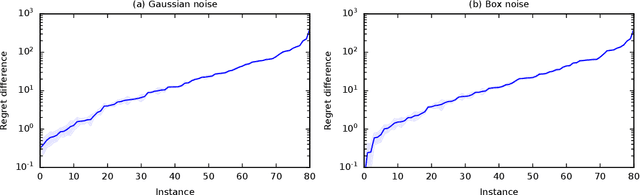
We derive the first finite-time logarithmic regret bounds for Bayesian bandits. For Gaussian bandits, we obtain a $O(c_h \log^2 n)$ bound, where $c_h$ is a prior-dependent constant. This matches the asymptotic lower bound of Lai (1987). Our proofs mark a technical departure from prior works, and are simple and general. To show generality, we apply our technique to linear bandits. Our bounds shed light on the value of the prior in the Bayesian setting, both in the objective and as a side information given to the learner. They significantly improve the $\tilde{O}(\sqrt{n})$ bounds, that despite the existing lower bounds, have become standard in the literature.

Bayesian Fixed-Budget Best-Arm Identification

Fixed-budget best-arm identification (BAI) is a bandit problem where the learning agent maximizes the probability of identifying the optimal arm after a fixed number of observations. In this work, we initiate the study of this problem in the Bayesian setting. We propose a Bayesian elimination algorithm and derive an upper bound on the probability that it fails to identify the optimal arm. The bound reflects the quality of the prior and is the first such bound in this setting. We prove it using a frequentist-like argument, where we carry the prior through, and then integrate out the random bandit instance at the end. Our upper bound asymptotically matches a newly established lower bound for $2$ arms. Our experimental results show that Bayesian elimination is superior to frequentist methods and competitive with the state-of-the-art Bayesian algorithms that have no guarantees in our setting.

Contextual Pandora's Box

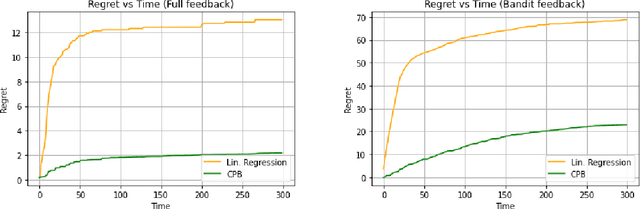
Pandora's Box is a fundamental stochastic optimization problem, where the decision-maker must find a good alternative while minimizing the search cost of exploring the value of each alternative. In the original formulation, it is assumed that accurate priors are given for the values of all the alternatives, while recent work studies the online variant of Pandora's Box where priors are originally unknown. In this work, we extend Pandora's Box to the online setting, while incorporating context. At every round, we are presented with a number of alternatives each having a context, an exploration cost and an unknown value drawn from an unknown prior distribution that may change at every round. Our main result is a no-regret algorithm that performs comparably well to the optimal algorithm which knows all prior distributions exactly. Our algorithm works even in the bandit setting where the algorithm never learns the values of the alternatives that were not explored. The key technique that enables our result is novel a modification of the realizability condition in contextual bandits that connects a context to the reservation value of the corresponding distribution rather than its mean

Towards Statistical and Computational Complexities of Polyak Step Size Gradient Descent

We study the statistical and computational complexities of the Polyak step size gradient descent algorithm under generalized smoothness and Lojasiewicz conditions of the population loss function, namely, the limit of the empirical loss function when the sample size goes to infinity, and the stability between the gradients of the empirical and population loss functions, namely, the polynomial growth on the concentration bound between the gradients of sample and population loss functions. We demonstrate that the Polyak step size gradient descent iterates reach a final statistical radius of convergence around the true parameter after logarithmic number of iterations in terms of the sample size. It is computationally cheaper than the polynomial number of iterations on the sample size of the fixed-step size gradient descent algorithm to reach the same final statistical radius when the population loss function is not locally strongly convex. Finally, we illustrate our general theory under three statistical examples: generalized linear model, mixture model, and mixed linear regression model.

Combinatorial Blocking Bandits with Stochastic Delays

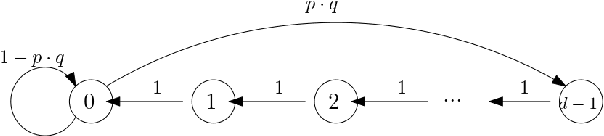
Recent work has considered natural variations of the multi-armed bandit problem, where the reward distribution of each arm is a special function of the time passed since its last pulling. In this direction, a simple (yet widely applicable) model is that of blocking bandits, where an arm becomes unavailable for a deterministic number of rounds after each play. In this work, we extend the above model in two directions: (i) We consider the general combinatorial setting where more than one arms can be played at each round, subject to feasibility constraints. (ii) We allow the blocking time of each arm to be stochastic. We first study the computational/unconditional hardness of the above setting and identify the necessary conditions for the problem to become tractable (even in an approximate sense). Based on these conditions, we provide a tight analysis of the approximation guarantee of a natural greedy heuristic that always plays the maximum expected reward feasible subset among the available (non-blocked) arms. When the arms' expected rewards are unknown, we adapt the above heuristic into a bandit algorithm, based on UCB, for which we provide sublinear (approximate) regret guarantees, matching the theoretical lower bounds in the limiting case of absence of delays.