Evangelia Gergatsouli
Contextual Pandora's Box
May 26, 2022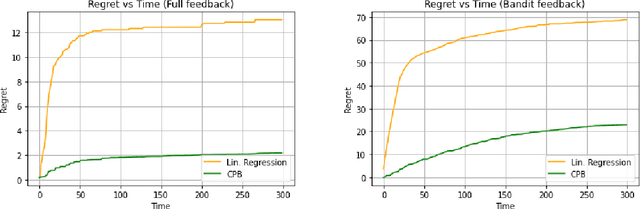
Abstract:Pandora's Box is a fundamental stochastic optimization problem, where the decision-maker must find a good alternative while minimizing the search cost of exploring the value of each alternative. In the original formulation, it is assumed that accurate priors are given for the values of all the alternatives, while recent work studies the online variant of Pandora's Box where priors are originally unknown. In this work, we extend Pandora's Box to the online setting, while incorporating context. At every round, we are presented with a number of alternatives each having a context, an exploration cost and an unknown value drawn from an unknown prior distribution that may change at every round. Our main result is a no-regret algorithm that performs comparably well to the optimal algorithm which knows all prior distributions exactly. Our algorithm works even in the bandit setting where the algorithm never learns the values of the alternatives that were not explored. The key technique that enables our result is novel a modification of the realizability condition in contextual bandits that connects a context to the reservation value of the corresponding distribution rather than its mean
Online Learning for Min Sum Set Cover and Pandora's Box
Feb 10, 2022Abstract:Two central problems in Stochastic Optimization are Min Sum Set Cover and Pandora's Box. In Pandora's Box, we are presented with n boxes, each containing an unknown value and the goal is to open the boxes in some order to minimize the sum of the search cost and the smallest value found. Given a distribution of value vectors, we are asked to identify a near-optimal search order. Min Sum Set Cover corresponds to the case where values are either 0 or infinity. In this work, we study the case where the value vectors are not drawn from a distribution but are presented to a learner in an online fashion. We present a computationally efficient algorithm that is constant-competitive against the cost of the optimal search order. We extend our results to a bandit setting where only the values of the boxes opened are revealed to the learner after every round. We also generalize our results to other commonly studied variants of Pandora's Box and Min Sum Set Cover that involve selecting more than a single value subject to a matroid constraint.
Approximating Pandora's Box with Correlations
Aug 30, 2021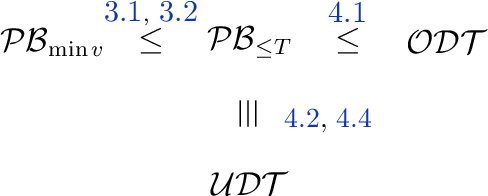
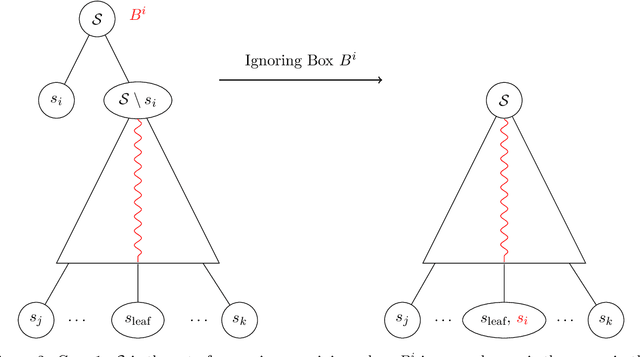
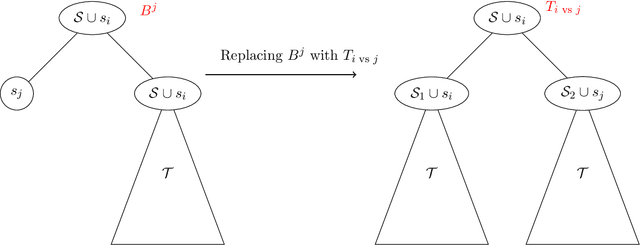
Abstract:The Pandora's Box problem asks to find a search strategy over $n$ alternatives given stochastic information about their values, aiming to minimize the sum of the search cost and the value of the chosen alternative. Even though the case of independently distributed values is well understood, our algorithmic understanding of the problem is very limited once the independence assumption is dropped. Our work aims to characterize the complexity of approximating the Pandora's Box problem under correlated value distributions. To that end, we present a general reduction to a simpler version of Pandora's Box, that only asks to find a value below a certain threshold, and eliminates the need to reason about future values that will arise during the search. Using this general tool, we study two cases of correlation; the case of explicitly given distributions of support $m$ and the case of mixtures of $m$ product distributions. $\bullet$ In the first case, we connect Pandora's Box to the well studied problem of Optimal Decision Tree, obtaining an $O(\log m)$ approximation but also showing that the problem is strictly easier as it is equivalent (up to constant factors) to the Uniform Decision Tree problem. $\bullet$ In the case of mixtures of product distributions, the problem is again related to the noisy variant of Optimal Decision Tree which is significantly more challenging. We give a constant-factor approximation that runs in time $n^{ \tilde O( m^2/\varepsilon^2 ) }$ for $m$ mixture components whose marginals on every alternative are either identical or separated in TV distance by $\varepsilon$.
Learning Augmented Online Facility Location
Jul 17, 2021



Abstract:Following the research agenda initiated by Munoz & Vassilvitskii [1] and Lykouris & Vassilvitskii [2] on learning-augmented online algorithms for classical online optimization problems, in this work, we consider the Online Facility Location problem under this framework. In Online Facility Location (OFL), demands arrive one-by-one in a metric space and must be (irrevocably) assigned to an open facility upon arrival, without any knowledge about future demands. We present an online algorithm for OFL that exploits potentially imperfect predictions on the locations of the optimal facilities. We prove that the competitive ratio decreases smoothly from sublogarithmic in the number of demands to constant, as the error, i.e., the total distance of the predicted locations to the optimal facility locations, decreases towards zero. We complement our analysis with a matching lower bound establishing that the dependence of the algorithm's competitive ratio on the error is optimal, up to constant factors. Finally, we evaluate our algorithm on real world data and compare our learning augmented approach with the current best online algorithm for the problem.
Black-box Methods for Restoring Monotonicity
Mar 21, 2020
Abstract:In many practical applications, heuristic or approximation algorithms are used to efficiently solve the task at hand. However their solutions frequently do not satisfy natural monotonicity properties of optimal solutions. In this work we develop algorithms that are able to restore monotonicity in the parameters of interest. Specifically, given oracle access to a (possibly non-monotone) multi-dimensional real-valued function $f$, we provide an algorithm that restores monotonicity while degrading the expected value of the function by at most $\varepsilon$. The number of queries required is at most logarithmic in $1/\varepsilon$ and exponential in the number of parameters. We also give a lower bound showing that this exponential dependence is necessary. Finally, we obtain improved query complexity bounds for restoring the weaker property of $k$-marginal monotonicity. Under this property, every $k$-dimensional projection of the function $f$ is required to be monotone. The query complexity we obtain only scales exponentially with $k$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge