Contextual Pandora's Box

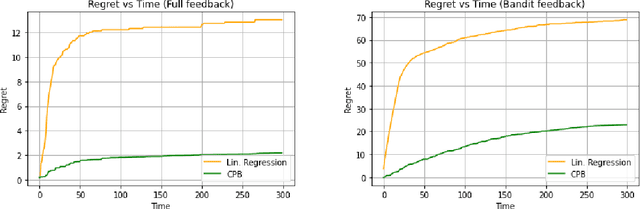
Pandora's Box is a fundamental stochastic optimization problem, where the decision-maker must find a good alternative while minimizing the search cost of exploring the value of each alternative. In the original formulation, it is assumed that accurate priors are given for the values of all the alternatives, while recent work studies the online variant of Pandora's Box where priors are originally unknown. In this work, we extend Pandora's Box to the online setting, while incorporating context. At every round, we are presented with a number of alternatives each having a context, an exploration cost and an unknown value drawn from an unknown prior distribution that may change at every round. Our main result is a no-regret algorithm that performs comparably well to the optimal algorithm which knows all prior distributions exactly. Our algorithm works even in the bandit setting where the algorithm never learns the values of the alternatives that were not explored. The key technique that enables our result is novel a modification of the realizability condition in contextual bandits that connects a context to the reservation value of the corresponding distribution rather than its mean