Anchored Diffusion Language Model

Diffusion Language Models (DLMs) promise parallel generation and bidirectional context, yet they underperform autoregressive (AR) models in both likelihood modeling and generated text quality. We identify that this performance gap arises when important tokens (e.g., key words or low-frequency words that anchor a sentence) are masked early in the forward process, limiting contextual information for accurate reconstruction. To address this, we introduce the Anchored Diffusion Language Model (ADLM), a novel two-stage framework that first predicts distributions over important tokens via an anchor network, and then predicts the likelihoods of missing tokens conditioned on the anchored predictions. ADLM significantly improves test perplexity on LM1B and OpenWebText, achieving up to 25.4% gains over prior DLMs, and narrows the gap with strong AR baselines. It also achieves state-of-the-art performance in zero-shot generalization across seven benchmarks and surpasses AR models in MAUVE score, which marks the first time a DLM generates better human-like text than an AR model. Theoretically, we derive an Anchored Negative Evidence Lower Bound (ANELBO) objective and show that anchoring improves sample complexity and likelihood modeling. Beyond diffusion, anchoring boosts performance in AR models and enhances reasoning in math and logic tasks, outperforming existing chain-of-thought approaches

Asymptotically-Optimal Gaussian Bandits with Side Observations

We study the problem of Gaussian bandits with general side information, as first introduced by Wu, Szepesvari, and Gyorgy. In this setting, the play of an arm reveals information about other arms, according to an arbitrary a priori known side information matrix: each element of this matrix encodes the fidelity of the information that the ``row'' arm reveals about the ``column'' arm. In the case of Gaussian noise, this model subsumes standard bandits, full-feedback, and graph-structured feedback as special cases. In this work, we first construct an LP-based asymptotic instance-dependent lower bound on the regret. The LP optimizes the cost (regret) required to reliably estimate the suboptimality gap of each arm. This LP lower bound motivates our main contribution: the first known asymptotically optimal algorithm for this general setting.

On Mitigating Affinity Bias through Bandits with Evolving Biased Feedback

Unconscious bias has been shown to influence how we assess our peers, with consequences for hiring, promotions and admissions. In this work, we focus on affinity bias, the component of unconscious bias which leads us to prefer people who are similar to us, despite no deliberate intention of favoritism. In a world where the people hired today become part of the hiring committee of tomorrow, we are particularly interested in understanding (and mitigating) how affinity bias affects this feedback loop. This problem has two distinctive features: 1) we only observe the biased value of a candidate, but we want to optimize with respect to their real value 2) the bias towards a candidate with a specific set of traits depends on the fraction of people in the hiring committee with the same set of traits. We introduce a new bandits variant that exhibits those two features, which we call affinity bandits. Unsurprisingly, classical algorithms such as UCB often fail to identify the best arm in this setting. We prove a new instance-dependent regret lower bound, which is larger than that in the standard bandit setting by a multiplicative function of $K$. Since we treat rewards that are time-varying and dependent on the policy's past actions, deriving this lower bound requires developing proof techniques beyond the standard bandit techniques. Finally, we design an elimination-style algorithm which nearly matches this regret, despite never observing the real rewards.

Optimization Can Learn Johnson Lindenstrauss Embeddings

Embeddings play a pivotal role across various disciplines, offering compact representations of complex data structures. Randomized methods like Johnson-Lindenstrauss (JL) provide state-of-the-art and essentially unimprovable theoretical guarantees for achieving such representations. These guarantees are worst-case and in particular, neither the analysis, nor the algorithm, takes into account any potential structural information of the data. The natural question is: must we randomize? Could we instead use an optimization-based approach, working directly with the data? A first answer is no: as we show, the distance-preserving objective of JL has a non-convex landscape over the space of projection matrices, with many bad stationary points. But this is not the final answer. We present a novel method motivated by diffusion models, that circumvents this fundamental challenge: rather than performing optimization directly over the space of projection matrices, we use optimization over the larger space of random solution samplers, gradually reducing the variance of the sampler. We show that by moving through this larger space, our objective converges to a deterministic (zero variance) solution, avoiding bad stationary points. This method can also be seen as an optimization-based derandomization approach and is an idea and method that we believe can be applied to many other problems.

Semantic Image Inversion and Editing using Rectified Stochastic Differential Equations

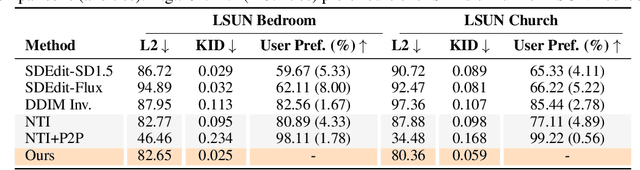
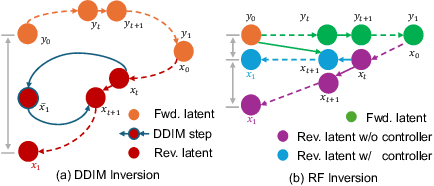
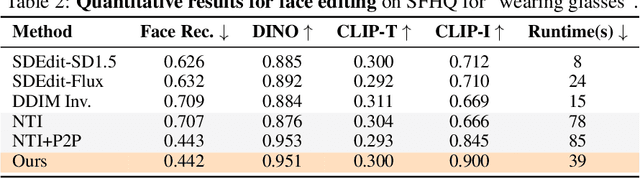
Generative models transform random noise into images; their inversion aims to transform images back to structured noise for recovery and editing. This paper addresses two key tasks: (i) inversion and (ii) editing of a real image using stochastic equivalents of rectified flow models (such as Flux). Although Diffusion Models (DMs) have recently dominated the field of generative modeling for images, their inversion presents faithfulness and editability challenges due to nonlinearities in drift and diffusion. Existing state-of-the-art DM inversion approaches rely on training of additional parameters or test-time optimization of latent variables; both are expensive in practice. Rectified Flows (RFs) offer a promising alternative to diffusion models, yet their inversion has been underexplored. We propose RF inversion using dynamic optimal control derived via a linear quadratic regulator. We prove that the resulting vector field is equivalent to a rectified stochastic differential equation. Additionally, we extend our framework to design a stochastic sampler for Flux. Our inversion method allows for state-of-the-art performance in zero-shot inversion and editing, outperforming prior works in stroke-to-image synthesis and semantic image editing, with large-scale human evaluations confirming user preference.

RL in Latent MDPs is Tractable: Online Guarantees via Off-Policy Evaluation

In many real-world decision problems there is partially observed, hidden or latent information that remains fixed throughout an interaction. Such decision problems can be modeled as Latent Markov Decision Processes (LMDPs), where a latent variable is selected at the beginning of an interaction and is not disclosed to the agent. In the last decade, there has been significant progress in solving LMDPs under different structural assumptions. However, for general LMDPs, there is no known learning algorithm that provably matches the existing lower bound~\cite{kwon2021rl}. We introduce the first sample-efficient algorithm for LMDPs without any additional structural assumptions. Our result builds off a new perspective on the role of off-policy evaluation guarantees and coverage coefficients in LMDPs, a perspective, that has been overlooked in the context of exploration in partially observed environments. Specifically, we establish a novel off-policy evaluation lemma and introduce a new coverage coefficient for LMDPs. Then, we show how these can be used to derive near-optimal guarantees of an optimistic exploration algorithm. These results, we believe, can be valuable for a wide range of interactive learning problems beyond LMDPs, and especially, for partially observed environments.

RB-Modulation: Training-Free Personalization of Diffusion Models using Stochastic Optimal Control

We propose Reference-Based Modulation (RB-Modulation), a new plug-and-play solution for training-free personalization of diffusion models. Existing training-free approaches exhibit difficulties in (a) style extraction from reference images in the absence of additional style or content text descriptions, (b) unwanted content leakage from reference style images, and (c) effective composition of style and content. RB-Modulation is built on a novel stochastic optimal controller where a style descriptor encodes the desired attributes through a terminal cost. The resulting drift not only overcomes the difficulties above, but also ensures high fidelity to the reference style and adheres to the given text prompt. We also introduce a cross-attention-based feature aggregation scheme that allows RB-Modulation to decouple content and style from the reference image. With theoretical justification and empirical evidence, our framework demonstrates precise extraction and control of content and style in a training-free manner. Further, our method allows a seamless composition of content and style, which marks a departure from the dependency on external adapters or ControlNets.

Beyond First-Order Tweedie: Solving Inverse Problems using Latent Diffusion

Sampling from the posterior distribution poses a major computational challenge in solving inverse problems using latent diffusion models. Common methods rely on Tweedie's first-order moments, which are known to induce a quality-limiting bias. Existing second-order approximations are impractical due to prohibitive computational costs, making standard reverse diffusion processes intractable for posterior sampling. This paper introduces Second-order Tweedie sampler from Surrogate Loss (STSL), a novel sampler that offers efficiency comparable to first-order Tweedie with a tractable reverse process using second-order approximation. Our theoretical results reveal that the second-order approximation is lower bounded by our surrogate loss that only requires $O(1)$ compute using the trace of the Hessian, and by the lower bound we derive a new drift term to make the reverse process tractable. Our method surpasses SoTA solvers PSLD and P2L, achieving 4X and 8X reduction in neural function evaluations, respectively, while notably enhancing sampling quality on FFHQ, ImageNet, and COCO benchmarks. In addition, we show STSL extends to text-guided image editing and addresses residual distortions present from corrupted images in leading text-guided image editing methods. To our best knowledge, this is the first work to offer an efficient second-order approximation in solving inverse problems using latent diffusion and editing real-world images with corruptions.

Prospective Side Information for Latent MDPs

In many interactive decision-making settings, there is latent and unobserved information that remains fixed. Consider, for example, a dialogue system, where complete information about a user, such as the user's preferences, is not given. In such an environment, the latent information remains fixed throughout each episode, since the identity of the user does not change during an interaction. This type of environment can be modeled as a Latent Markov Decision Process (LMDP), a special instance of Partially Observed Markov Decision Processes (POMDPs). Previous work established exponential lower bounds in the number of latent contexts for the LMDP class. This puts forward a question: under which natural assumptions a near-optimal policy of an LMDP can be efficiently learned? In this work, we study the class of LMDPs with {\em prospective side information}, when an agent receives additional, weakly revealing, information on the latent context at the beginning of each episode. We show that, surprisingly, this problem is not captured by contemporary settings and algorithms designed for partially observed environments. We then establish that any sample efficient algorithm must suffer at least $\Omega(K^{2/3})$-regret, as opposed to standard $\Omega(\sqrt{K})$ lower bounds, and design an algorithm with a matching upper bound.

Optimizing Solution-Samplers for Combinatorial Problems: The Landscape of Policy-Gradient Methods

Deep Neural Networks and Reinforcement Learning methods have empirically shown great promise in tackling challenging combinatorial problems. In those methods a deep neural network is used as a solution generator which is then trained by gradient-based methods (e.g., policy gradient) to successively obtain better solution distributions. In this work we introduce a novel theoretical framework for analyzing the effectiveness of such methods. We ask whether there exist generative models that (i) are expressive enough to generate approximately optimal solutions; (ii) have a tractable, i.e, polynomial in the size of the input, number of parameters; (iii) their optimization landscape is benign in the sense that it does not contain sub-optimal stationary points. Our main contribution is a positive answer to this question. Our result holds for a broad class of combinatorial problems including Max- and Min-Cut, Max-$k$-CSP, Maximum-Weight-Bipartite-Matching, and the Traveling Salesman Problem. As a byproduct of our analysis we introduce a novel regularization process over vanilla gradient descent and provide theoretical and experimental evidence that it helps address vanishing-gradient issues and escape bad stationary points.