Logarithmic Bayes Regret Bounds

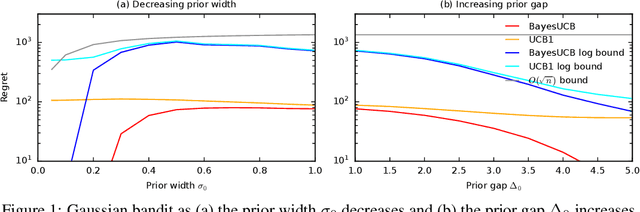
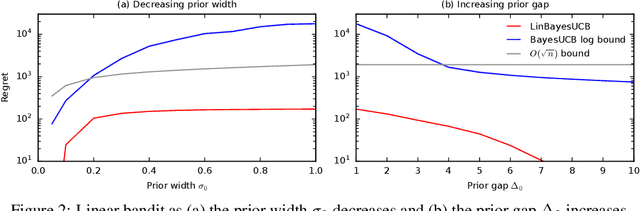
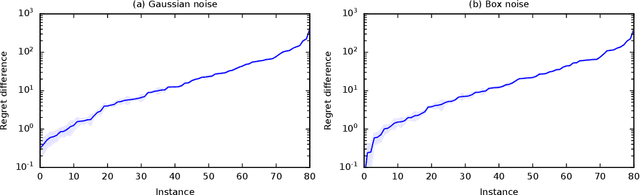
We derive the first finite-time logarithmic regret bounds for Bayesian bandits. For Gaussian bandits, we obtain a $O(c_h \log^2 n)$ bound, where $c_h$ is a prior-dependent constant. This matches the asymptotic lower bound of Lai (1987). Our proofs mark a technical departure from prior works, and are simple and general. To show generality, we apply our technique to linear bandits. Our bounds shed light on the value of the prior in the Bayesian setting, both in the objective and as a side information given to the learner. They significantly improve the $\tilde{O}(\sqrt{n})$ bounds, that despite the existing lower bounds, have become standard in the literature.

Selective Uncertainty Propagation in Offline RL

We study the finite-horizon offline reinforcement learning (RL) problem. Since actions at any state can affect next-state distributions, the related distributional shift challenges can make this problem far more statistically complex than offline policy learning for a finite sequence of stochastic contextual bandit environments. We formalize this insight by showing that the statistical hardness of offline RL instances can be measured by estimating the size of actions' impact on next-state distributions. Furthermore, this estimated impact allows us to propagate just enough value function uncertainty from future steps to avoid model exploitation, enabling us to develop algorithms that improve upon traditional pessimistic approaches for offline RL on statistically simple instances. Our approach is supported by theory and simulations.

Multi-Task Off-Policy Learning from Bandit Feedback

Many practical applications, such as recommender systems and learning to rank, involve solving multiple similar tasks. One example is learning of recommendation policies for users with similar movie preferences, where the users may still rank the individual movies slightly differently. Such tasks can be organized in a hierarchy, where similar tasks are related through a shared structure. In this work, we formulate this problem as a contextual off-policy optimization in a hierarchical graphical model from logged bandit feedback. To solve the problem, we propose a hierarchical off-policy optimization algorithm (HierOPO), which estimates the parameters of the hierarchical model and then acts pessimistically with respect to them. We instantiate HierOPO in linear Gaussian models, for which we also provide an efficient implementation and analysis. We prove per-task bounds on the suboptimality of the learned policies, which show a clear improvement over not using the hierarchical model. We also evaluate the policies empirically. Our theoretical and empirical results show a clear advantage of using the hierarchy over solving each task independently.

Bayesian Fixed-Budget Best-Arm Identification

Fixed-budget best-arm identification (BAI) is a bandit problem where the learning agent maximizes the probability of identifying the optimal arm after a fixed number of observations. In this work, we initiate the study of this problem in the Bayesian setting. We propose a Bayesian elimination algorithm and derive an upper bound on the probability that it fails to identify the optimal arm. The bound reflects the quality of the prior and is the first such bound in this setting. We prove it using a frequentist-like argument, where we carry the prior through, and then integrate out the random bandit instance at the end. Our upper bound asymptotically matches a newly established lower bound for $2$ arms. Our experimental results show that Bayesian elimination is superior to frequentist methods and competitive with the state-of-the-art Bayesian algorithms that have no guarantees in our setting.

Generalizing Hierarchical Bayesian Bandits

A contextual bandit is a popular and practical framework for online learning to act under uncertainty. In many problems, the number of actions is huge and their mean rewards are correlated. In this work, we introduce a general framework for capturing such correlations through a two-level graphical model where actions are related through multiple shared latent parameters. We propose a Thompson sampling algorithm G-HierTS that uses this structure to explore efficiently and bound its Bayes regret. The regret has two terms, one for learning action parameters and the other for learning the shared latent parameters. The terms reflect the structure of our model as well as the quality of priors. Our theoretical findings are validated empirically using both synthetic and real-world problems. We also experiment with G-HierTS that maintains a factored posterior over latent parameters. While this approximation does not come with guarantees, it improves computational efficiency with a minimal impact on empirical regret.

Meta-Learning for Simple Regret Minimization

We develop a meta-learning framework for simple regret minimization in bandits. In this framework, a learning agent interacts with a sequence of bandit tasks, which are sampled i.i.d.\ from an unknown prior distribution, and learns its meta-parameters to perform better on future tasks. We propose the first Bayesian and frequentist algorithms for this meta-learning problem. The Bayesian algorithm has access to a prior distribution over the meta-parameters and its meta simple regret over $m$ bandit tasks with horizon $n$ is mere $\tilde{O}(m / \sqrt{n})$. This is while we show that the meta simple regret of the frequentist algorithm is $\tilde{O}(\sqrt{m} n + m/ \sqrt{n})$, and thus, worse. However, the algorithm is more general, because it does not need a prior distribution over the meta-parameters, and is easier to implement for various distributions. We instantiate our algorithms for several classes of bandit problems. Our algorithms are general and we complement our theory by evaluating them empirically in several environments.

Task-Agnostic Graph Explanations

Graph Neural Networks (GNNs) have emerged as powerful tools to encode graph structured data. Due to their broad applications, there is an increasing need to develop tools to explain how GNNs make decisions given graph structured data. Existing learning-based GNN explanation approaches are task-specific in training and hence suffer from crucial drawbacks. Specifically, they are incapable of producing explanations for a multitask prediction model with a single explainer. They are also unable to provide explanations in cases where the GNN is trained in a self-supervised manner, and the resulting representations are used in future downstream tasks. To address these limitations, we propose a Task-Agnostic GNN Explainer (TAGE) trained under self-supervision with no knowledge of downstream tasks. TAGE enables the explanation of GNN embedding models without downstream tasks and allows efficient explanation of multitask models. Our extensive experiments show that TAGE can significantly speed up the explanation efficiency by using the same model to explain predictions for multiple downstream tasks while achieving explanation quality as good as or even better than current state-of-the-art GNN explanation approaches.

Deep Hierarchy in Bandits

Mean rewards of actions are often correlated. The form of these correlations may be complex and unknown a priori, such as the preferences of a user for recommended products and their categories. To maximize statistical efficiency, it is important to leverage these correlations when learning. We formulate a bandit variant of this problem where the correlations of mean action rewards are represented by a hierarchical Bayesian model with latent variables. Since the hierarchy can have multiple layers, we call it deep. We propose a hierarchical Thompson sampling algorithm (HierTS) for this problem, and show how to implement it efficiently for Gaussian hierarchies. The efficient implementation is possible due to a novel exact hierarchical representation of the posterior, which itself is of independent interest. We use this exact posterior to analyze the Bayes regret of HierTS in Gaussian bandits. Our analysis reflects the structure of the problem, that the regret decreases with the prior width, and also shows that hierarchies reduce the regret by non-constant factors in the number of actions. We confirm these theoretical findings empirically, in both synthetic and real-world experiments.

Cold Brew: Distilling Graph Node Representations with Incomplete or Missing Neighborhoods

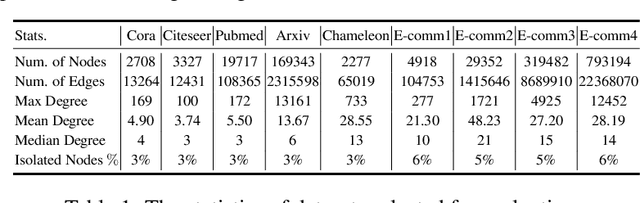
Graph Neural Networks (GNNs) have achieved state of the art performance in node classification, regression, and recommendation tasks. GNNs work well when high-quality and rich connectivity structure is available. However, this requirement is not satisfied in many real world graphs where the node degrees have power-law distributions as many nodes have either fewer or noisy connections. The extreme case of this situation is a node may have no neighbors at all, called Strict Cold Start (SCS) scenario. This forces the prediction models to rely completely on the node's input features. We propose Cold Brew to address the SCS and noisy neighbor setting compared to pointwise and other graph-based models via a distillation approach. We introduce feature-contribution ratio (FCR), a metric to study the viability of using inductive GNNs to solve the SCS problem and to select the best architecture for SCS generalization. We experimentally show FCR disentangles the contributions of various components of graph datasets and demonstrate the superior performance of Cold Brew on several public benchmarks and proprietary e-commerce datasets. The source code for our approach is available at: https://github.com/amazon-research/gnn-tail-generalization.

Probabilistic Entity Representation Model for Reasoning over Knowledge Graphs

Logical reasoning over Knowledge Graphs (KGs) is a fundamental technique that can provide efficient querying mechanism over large and incomplete databases. Current approaches employ spatial geometries such as boxes to learn query representations that encompass the answer entities and model the logical operations of projection and intersection. However, their geometry is restrictive and leads to non-smooth strict boundaries, which further results in ambiguous answer entities. Furthermore, previous works propose transformation tricks to handle unions which results in non-closure and, thus, cannot be chained in a stream. In this paper, we propose a Probabilistic Entity Representation Model (PERM) to encode entities as a Multivariate Gaussian density with mean and covariance parameters to capture its semantic position and smooth decision boundary, respectively. Additionally, we also define the closed logical operations of projection, intersection, and union that can be aggregated using an end-to-end objective function. On the logical query reasoning problem, we demonstrate that the proposed PERM significantly outperforms the state-of-the-art methods on various public benchmark KG datasets on standard evaluation metrics. We also evaluate PERM's competence on a COVID-19 drug-repurposing case study and show that our proposed work is able to recommend drugs with substantially better F1 than current methods. Finally, we demonstrate the working of our PERM's query answering process through a low-dimensional visualization of the Gaussian representations.