Multi-Objective Optimization via Wasserstein-Fisher-Rao Gradient Flow

Multi-objective optimization (MOO) aims to optimize multiple, possibly conflicting objectives with widespread applications. We introduce a novel interacting particle method for MOO inspired by molecular dynamics simulations. Our approach combines overdamped Langevin and birth-death dynamics, incorporating a "dominance potential" to steer particles toward global Pareto optimality. In contrast to previous methods, our method is able to relocate dominated particles, making it particularly adept at managing Pareto fronts of complicated geometries. Our method is also theoretically grounded as a Wasserstein-Fisher-Rao gradient flow with convergence guarantees. Extensive experiments confirm that our approach outperforms state-of-the-art methods on challenging synthetic and real-world datasets.

Selective Uncertainty Propagation in Offline RL

We study the finite-horizon offline reinforcement learning (RL) problem. Since actions at any state can affect next-state distributions, the related distributional shift challenges can make this problem far more statistically complex than offline policy learning for a finite sequence of stochastic contextual bandit environments. We formalize this insight by showing that the statistical hardness of offline RL instances can be measured by estimating the size of actions' impact on next-state distributions. Furthermore, this estimated impact allows us to propagate just enough value function uncertainty from future steps to avoid model exploitation, enabling us to develop algorithms that improve upon traditional pessimistic approaches for offline RL on statistically simple instances. Our approach is supported by theory and simulations.

Multi-Player Bandits Robust to Adversarial Collisions

Motivated by cognitive radios, stochastic Multi-Player Multi-Armed Bandits has been extensively studied in recent years. In this setting, each player pulls an arm, and receives a reward corresponding to the arm if there is no collision, namely the arm was selected by one single player. Otherwise, the player receives no reward if collision occurs. In this paper, we consider the presence of malicious players (or attackers) who obstruct the cooperative players (or defenders) from maximizing their rewards, by deliberately colliding with them. We provide the first decentralized and robust algorithm RESYNC for defenders whose performance deteriorates gracefully as $\tilde{O}(C)$ as the number of collisions $C$ from the attackers increases. We show that this algorithm is order-optimal by proving a lower bound which scales as $\Omega(C)$. This algorithm is agnostic to the algorithm used by the attackers and agnostic to the number of collisions $C$ faced from attackers.

Understanding the Limits of Poisoning Attacks in Episodic Reinforcement Learning

To understand the security threats to reinforcement learning (RL) algorithms, this paper studies poisoning attacks to manipulate \emph{any} order-optimal learning algorithm towards a targeted policy in episodic RL and examines the potential damage of two natural types of poisoning attacks, i.e., the manipulation of \emph{reward} and \emph{action}. We discover that the effect of attacks crucially depend on whether the rewards are bounded or unbounded. In bounded reward settings, we show that only reward manipulation or only action manipulation cannot guarantee a successful attack. However, by combining reward and action manipulation, the adversary can manipulate any order-optimal learning algorithm to follow any targeted policy with $\tilde{\Theta}(\sqrt{T})$ total attack cost, which is order-optimal, without any knowledge of the underlying MDP. In contrast, in unbounded reward settings, we show that reward manipulation attacks are sufficient for an adversary to successfully manipulate any order-optimal learning algorithm to follow any targeted policy using $\tilde{O}(\sqrt{T})$ amount of contamination. Our results reveal useful insights about what can or cannot be achieved by poisoning attacks, and are set to spur more works on the design of robust RL algorithms.

Secure-UCB: Saving Stochastic Bandits from Poisoning Attacks via Limited Data Verification

This paper studies bandit algorithms under data poisoning attacks in a bounded reward setting. We consider a strong attacker model in which the attacker can observe both the selected actions and their corresponding rewards, and can contaminate the rewards with additive noise. We show that \emph{any} bandit algorithm with regret $O(\log T)$ can be forced to suffer a regret $\Omega(T)$ with an expected amount of contamination $O(\log T)$. This amount of contamination is also necessary, as we prove that there exists an $O(\log T)$ regret bandit algorithm, specifically the classical UCB, that requires $\Omega(\log T)$ amount of contamination to suffer regret $\Omega(T)$. To combat such poising attacks, our second main contribution is to propose a novel algorithm, Secure-UCB, which uses limited \emph{verification} to access a limited number of uncontaminated rewards. We show that with $O(\log T)$ expected number of verifications, Secure-UCB can restore the order optimal $O(\log T)$ regret \emph{irrespective of the amount of contamination} used by the attacker. Finally, we prove that for any bandit algorithm, this number of verifications $O(\log T)$ is necessary to recover the order-optimal regret. We can then conclude that Secure-UCB is order-optimal in terms of both the expected regret and the expected number of verifications, and can save stochastic bandits from any data poisoning attack.

Sequential Choice Bandits with Feedback for Personalizing users' experience

In this work, we study sequential choice bandits with feedback. We propose bandit algorithms for a platform that personalizes users' experience to maximize its rewards. For each action directed to a given user, the platform is given a positive reward, which is a non-decreasing function of the action, if this action is below the user's threshold. Users are equipped with a patience budget, and actions that are above the threshold decrease the user's patience. When all patience is lost, the user abandons the platform. The platform attempts to learn the thresholds of the users in order to maximize its rewards, based on two different feedback models describing the information pattern available to the platform at each action. We define a notion of regret by determining the best action to be taken when the platform knows that the user's threshold is in a given interval. We then propose bandit algorithms for the two feedback models and show that upper and lower bounds on the regret are of the order of $\tilde{O}(N^{2/3})$ and $\tilde\Omega(N^{2/3})$, respectively, where $N$ is the total number of users. Finally, we show that the waiting time of any user before receiving a personalized experience is uniform in $N$.

Learning-based attacks in Cyber-Physical Systems: Exploration, Detection, and Control Cost trade-offs

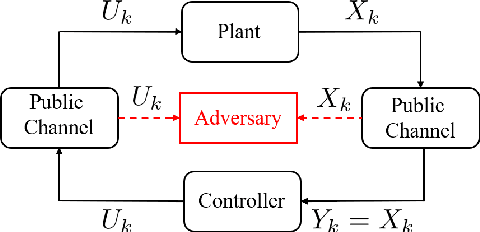
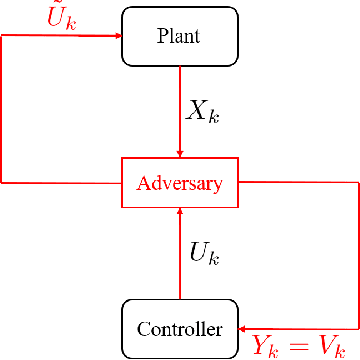
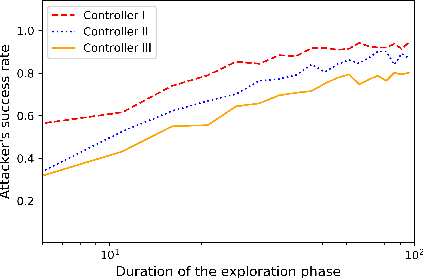
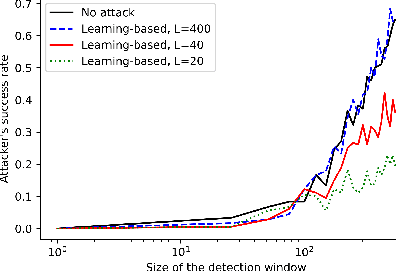
We study the problem of learning-based attacks in linear systems, where the communication channel between the controller and the plant can be hijacked by a malicious attacker. We assume the attacker learns the dynamics of the system from observations, then overrides the controller's actuation signal, while mimicking legitimate operation by providing fictitious sensor readings to the controller. On the other hand, the controller is on a lookout to detect the presence of the attacker and tries to enhance the detection performance by carefully crafting its control signals. We study the trade-offs between the information acquired by the attacker from observations, the detection capabilities of the controller, and the control cost. Specifically, we provide tight upper and lower bounds on the expected $\epsilon$-deception time, namely the time required by the controller to make a decision regarding the presence of an attacker with confidence at least $(1-\epsilon\log(1/\epsilon))$. We then show a probabilistic lower bound on the time that must be spent by the attacker learning the system, in order for the controller to have a given expected $\epsilon$-deception time. We show that this bound is also order optimal, in the sense that if the attacker satisfies it, then there exists a learning algorithm with the given order expected deception time. Finally, we show a lower bound on the expected energy expenditure required to guarantee detection with confidence at least $1-\epsilon \log(1/\epsilon)$.

Online learning with feedback graphs and switching costs

We study online learning when partial feedback information is provided following every action of the learning process, and the learner incurs switching costs for changing his actions. In this setting, the feedback information system can be represented by a graph, and previous work provided the expected regret of the learner in the case of a clique (Expert setup), or disconnected single loops (Multi-Armed Bandits). We provide a lower bound on the expected regret in the partial information (PI) setting, namely for general feedback graphs ---excluding the clique. We show that all algorithms that are optimal without switching costs are necessarily sub-optimal in the presence of switching costs, which motivates the need to design new algorithms in this setup. We propose two novel algorithms: Threshold Based EXP3 and EXP3.SC. For the two special cases of symmetric PI setting and Multi-Armed-Bandits, we show that the expected regret of both algorithms is order optimal in the duration of the learning process with a pre-constant dependent on the feedback system. Additionally, we show that Threshold Based EXP3 is order optimal in the switching cost, whereas EXP3.SC is not. Finally, empirical evaluations show that Threshold Based EXP3 outperforms previous algorithm EXP3 SET in the presence of switching costs, and Batch EXP3 in the special setting of Multi-Armed Bandits with switching costs, where both algorithms are order optimal.

Distributed Chernoff Test: Optimal decision systems over networks

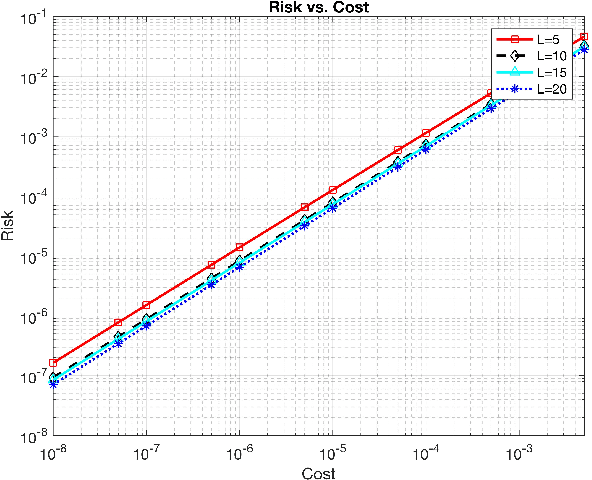
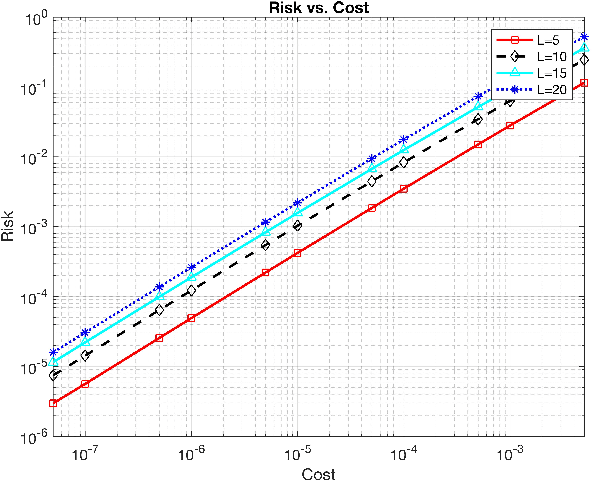
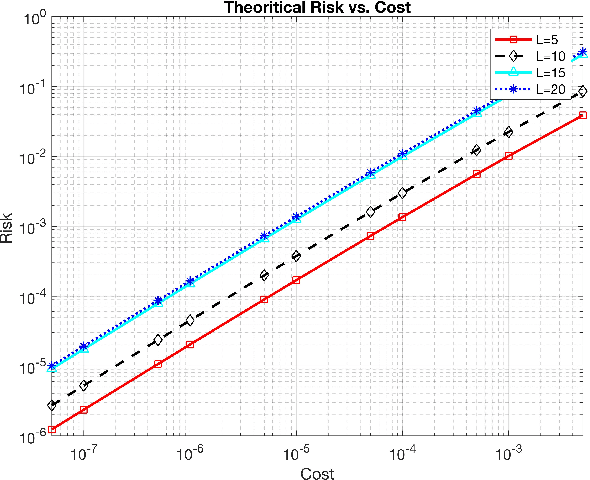
In this work, we propose two different sequential and adaptive hypothesis tests, motivated from classic Chernoff's test, for both decentralized and distributed setup of sensor networks. In the former setup, the sensors can communicate via central entity i.e. fusion center. On the other hand, in the latter setup, sensors are connected via communication link, and no central entity is present to facilitate the communication. We compare the performance of these tests with the optimal consistent sequential test in the sensor network. In decentralized setup, the proposed test achieves the same asymptotic optimality of the classic one, minimizing the expected cost required to reach a decision plus the expected cost of making a wrong decision, when the observation cost per unit time tends to zero. This test is also asymptotic optimal in the higher moments of decision time. The proposed test is parsimonious in terms of communications as the expected number of channel uses required by each sensor, in the regime of vanishing observation cost per unit time, to complete the test converges to four.In distributed setup, the proposed test is evaluated on the same performance measures as the test in decentralized setup. We also provide sufficient conditions for which the proposed test in distributed setup also achieves the same asymptotic optimality as the classic one. Like the proposed test in decentralized setup, under these sufficient conditions, the proposed test in distributed setup is also asymptotic optimal in the higher moments of time required to reach a decision in the sensor network. This test is parsimonious is terms of communications in comparison to the state of art schemes proposed in the literature for distributed hypothesis testing.