Particle Flows for Source Localization in 3-D Using TDOA Measurements

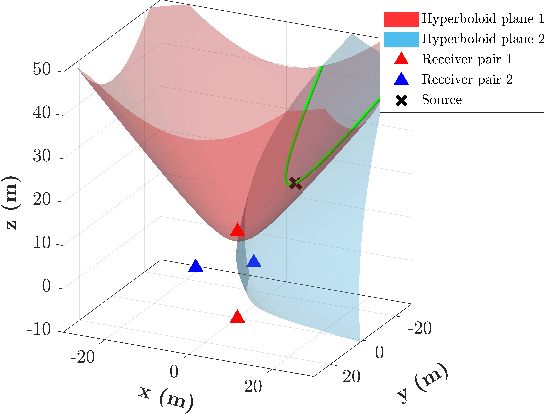
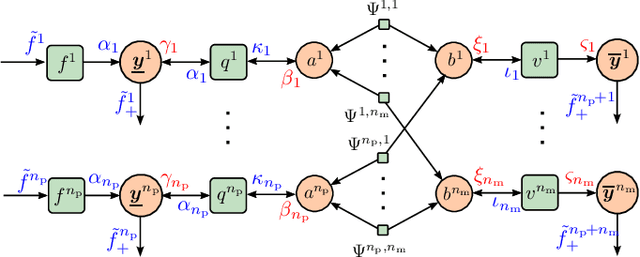
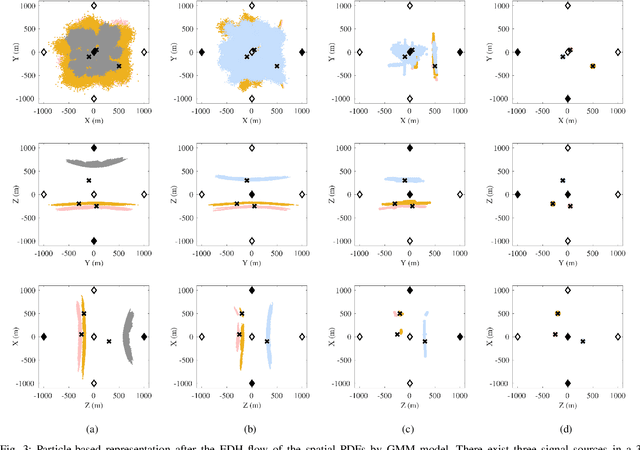
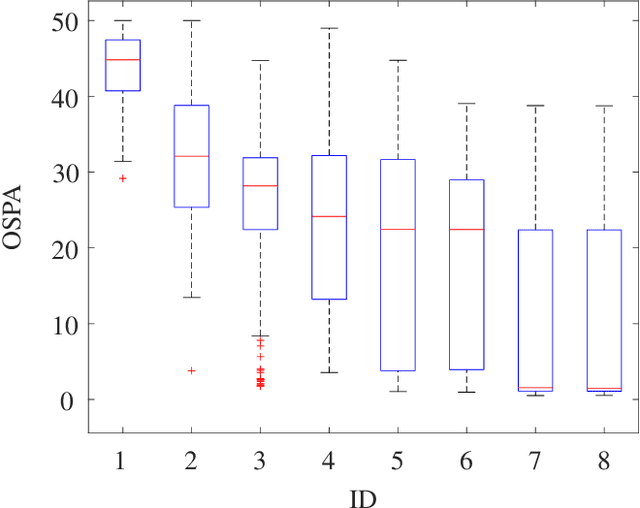
Localization using time-difference of arrival (TDOA) has myriad applications, e.g., in passive surveillance systems and marine mammal research. In this paper, we present a Bayesian estimation method that can localize an unknown number of static sources in 3-D based on TDOA measurements. The proposed localization algorithm based on particle flow (PFL) can overcome the challenges related to the highly nonlinear TDOA measurement model, the data association (DA) uncertainty, and the uncertainty in the number of sources to be localized. Different PFL strategies are compared within a unified belief propagation (BP) framework in a challenging multisensor source localization problem. In particular, we consider PFL-based approximation of beliefs based on one or multiple Gaussian kernels with parameters computed using deterministic and stochastic flow processes. Our numerical results demonstrate that the proposed method can correctly determine the number of sources and provide accurate location estimates. The stochastic flow demonstrates greater accuracy compared to the deterministic flow when using the same number of particles.

ISR: Invertible Symbolic Regression

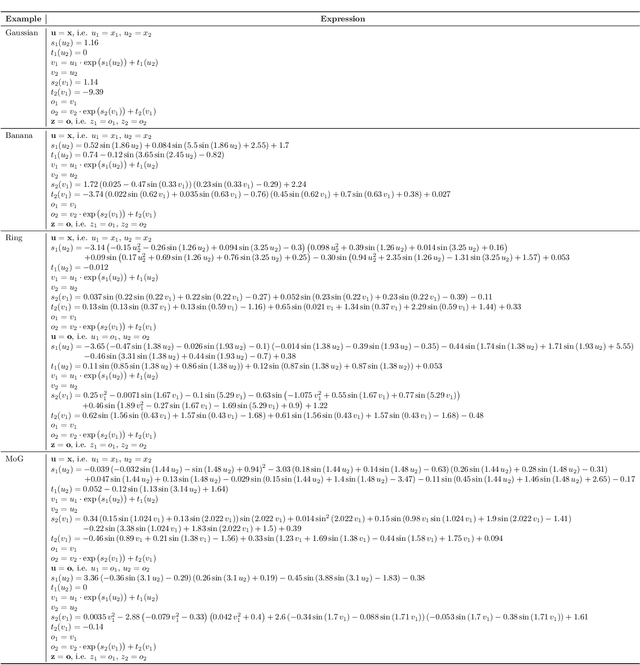
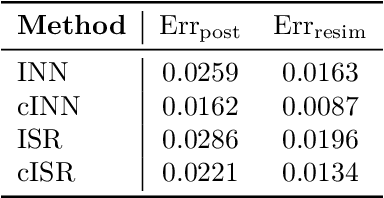
We introduce an Invertible Symbolic Regression (ISR) method. It is a machine learning technique that generates analytical relationships between inputs and outputs of a given dataset via invertible maps (or architectures). The proposed ISR method naturally combines the principles of Invertible Neural Networks (INNs) and Equation Learner (EQL), a neural network-based symbolic architecture for function learning. In particular, we transform the affine coupling blocks of INNs into a symbolic framework, resulting in an end-to-end differentiable symbolic invertible architecture that allows for efficient gradient-based learning. The proposed ISR framework also relies on sparsity promoting regularization, allowing the discovery of concise and interpretable invertible expressions. We show that ISR can serve as a (symbolic) normalizing flow for density estimation tasks. Furthermore, we highlight its practical applicability in solving inverse problems, including a benchmark inverse kinematics problem, and notably, a geoacoustic inversion problem in oceanography aimed at inferring posterior distributions of underlying seabed parameters from acoustic signals.

Uncertainty-aware Safe Exploratory Planning using Gaussian Process and Neural Control Contraction Metric

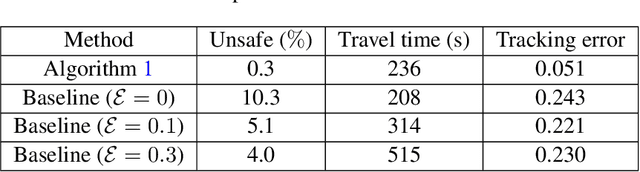
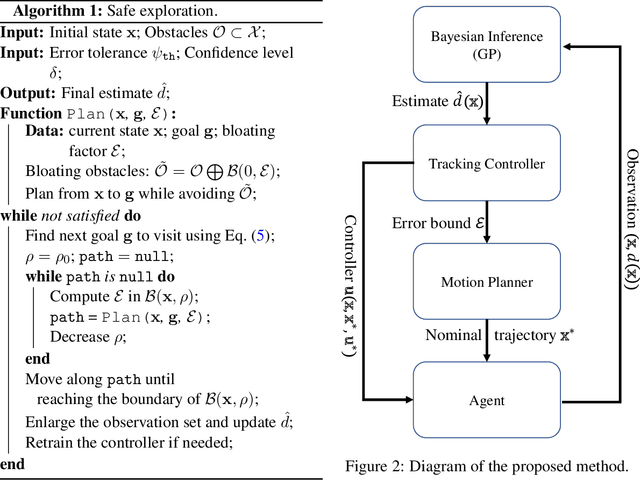
In this paper, we consider the problem of using a robot to explore an environment with an unknown, state-dependent disturbance function while avoiding some forbidden areas. The goal of the robot is to safely collect observations of the disturbance and construct an accurate estimate of the underlying disturbance function. We use Gaussian Process (GP) to get an estimate of the disturbance from data with a high-confidence bound on the regression error. Furthermore, we use neural Contraction Metrics to derive a tracking controller and the corresponding high-confidence uncertainty tube around the nominal trajectory planned for the robot, based on the estimate of the disturbance. From the robustness of the Contraction Metric, error bound can be pre-computed and used by the motion planner such that the actual trajectory is guaranteed to be safe. As the robot collects more and more observations along its trajectory, the estimate of the disturbance becomes more and more accurate, which in turn improves the performance of the tracking controller and enlarges the free space that the robot can safely explore. We evaluate the proposed method using a carefully designed environment with a ground vehicle. Results show that with the proposed method the robot can thoroughly explore the environment safely and quickly.

Control Barriers in Bayesian Learning of System Dynamics

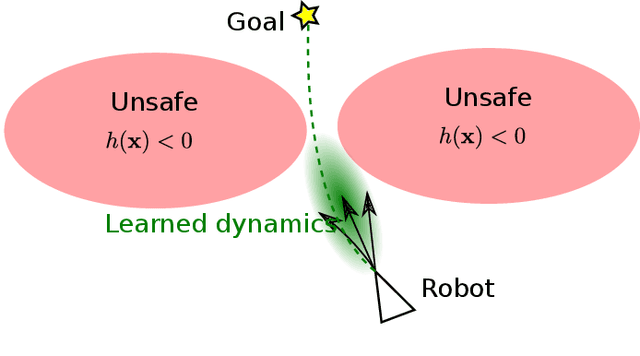
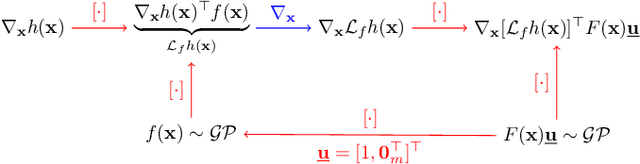
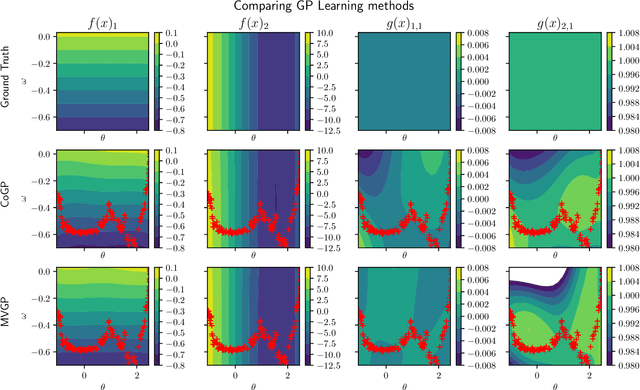
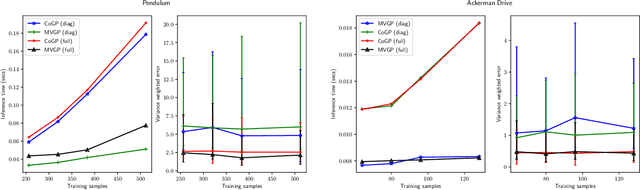
This paper focuses on learning a model of system dynamics online while satisfying safety constraints. Our objective is to avoid offline system identification or hand-specified models and allow a system to safely and autonomously estimate and adapt its own model during operation. Given streaming observations of the system state, we use Bayesian learning to obtain a distribution over the system dynamics. Specifically, we use a matrix variate Gaussian process (MVGP) regression approach with efficient covariance factorization to learn the drift and input gain terms of a nonlinear control-affine system. The MVGP distribution is then used to optimize the system behavior and ensure safety with high probability, by specifying control Lyapunov function (CLF) and control barrier function (CBF) chance constraints. We show that a safe control policy can be synthesized for systems with arbitrary relative degree and probabilistic CLF-CBF constraints by solving a second order cone program (SOCP). Finally, we extend our design to a self-triggering formulation, adaptively determining the time at which a new control input needs to be applied in order to guarantee safety.

Learning-based attacks in Cyber-Physical Systems: Exploration, Detection, and Control Cost trade-offs

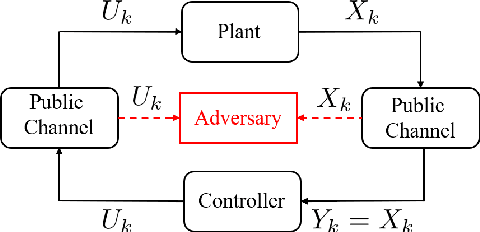
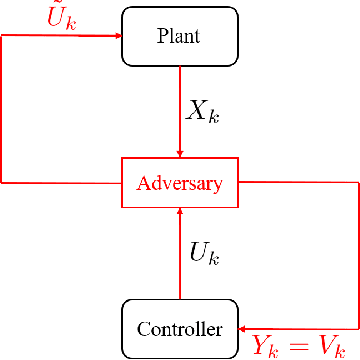
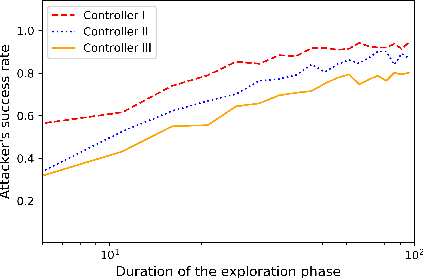
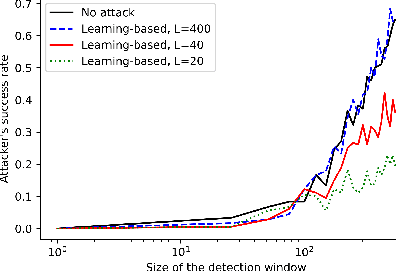
We study the problem of learning-based attacks in linear systems, where the communication channel between the controller and the plant can be hijacked by a malicious attacker. We assume the attacker learns the dynamics of the system from observations, then overrides the controller's actuation signal, while mimicking legitimate operation by providing fictitious sensor readings to the controller. On the other hand, the controller is on a lookout to detect the presence of the attacker and tries to enhance the detection performance by carefully crafting its control signals. We study the trade-offs between the information acquired by the attacker from observations, the detection capabilities of the controller, and the control cost. Specifically, we provide tight upper and lower bounds on the expected $\epsilon$-deception time, namely the time required by the controller to make a decision regarding the presence of an attacker with confidence at least $(1-\epsilon\log(1/\epsilon))$. We then show a probabilistic lower bound on the time that must be spent by the attacker learning the system, in order for the controller to have a given expected $\epsilon$-deception time. We show that this bound is also order optimal, in the sense that if the attacker satisfies it, then there exists a learning algorithm with the given order expected deception time. Finally, we show a lower bound on the expected energy expenditure required to guarantee detection with confidence at least $1-\epsilon \log(1/\epsilon)$.

Safe Multi-Agent Interaction through Robust Control Barrier Functions with Learned Uncertainties

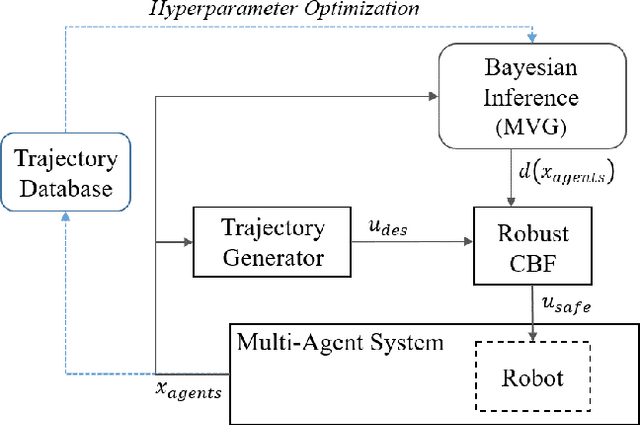
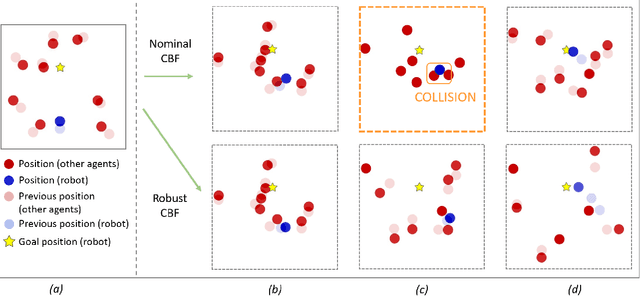
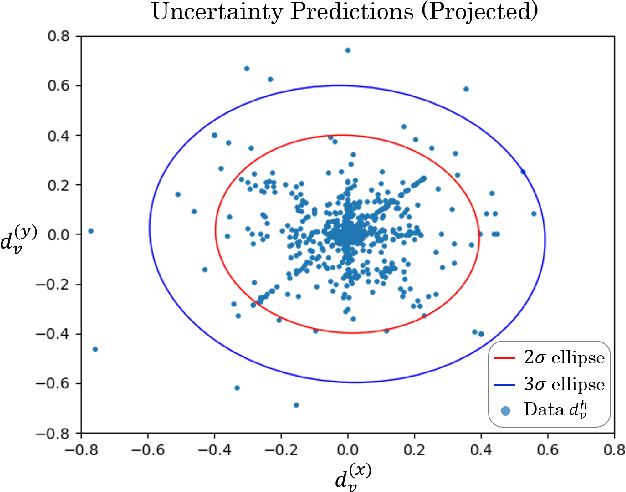
Robots operating in real world settings must navigate and maintain safety while interacting with many heterogeneous agents and obstacles. Multi-Agent Control Barrier Functions (CBF) have emerged as a computationally efficient tool to guarantee safety in multi-agent environments, but they assume perfect knowledge of both the robot dynamics and other agents' dynamics. While knowledge of the robot's dynamics might be reasonably well known, the heterogeneity of agents in real-world environments means there will always be considerable uncertainty in our prediction of other agents' dynamics. This work aims to learn high-confidence bounds for these dynamic uncertainties using Matrix-Variate Gaussian Process models, and incorporates them into a robust multi-agent CBF framework. We transform the resulting min-max robust CBF into a quadratic program, which can be efficiently solved in real time. We verify via simulation results that the nominal multi-agent CBF is often violated during agent interactions, whereas our robust formulation maintains safety with a much higher probability and adapts to learned uncertainties

Probabilistic Safety Constraints for Learned High Relative Degree System Dynamics

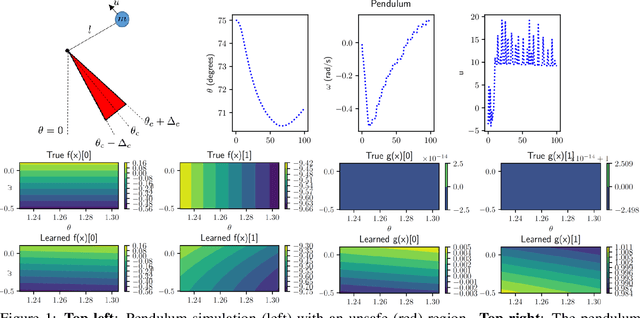
This paper focuses on learning a model of system dynamics online while satisfying safety constraints. Our motivation is to avoid offline system identification or hand-specified dynamics models and allow a system to safely and autonomously estimate and adapt its own model during online operation. Given streaming observations of the system state, we use Bayesian learning to obtain a distribution over the system dynamics. In turn, the distribution is used to optimize the system behavior and ensure safety with high probability, by specifying a chance constraint over a control barrier function.

Authentication of cyber-physical systems under learning-based attacks

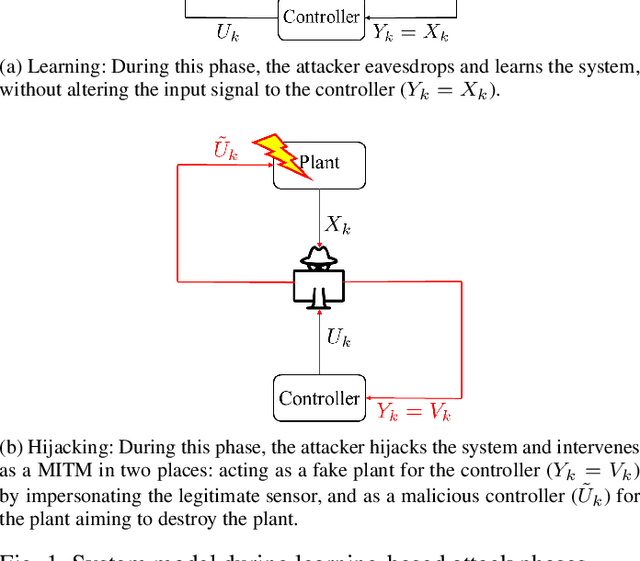
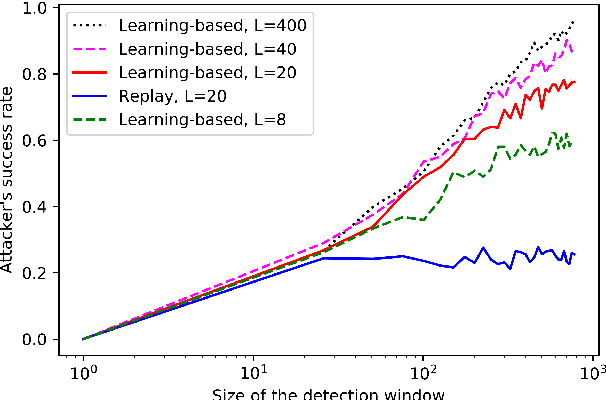
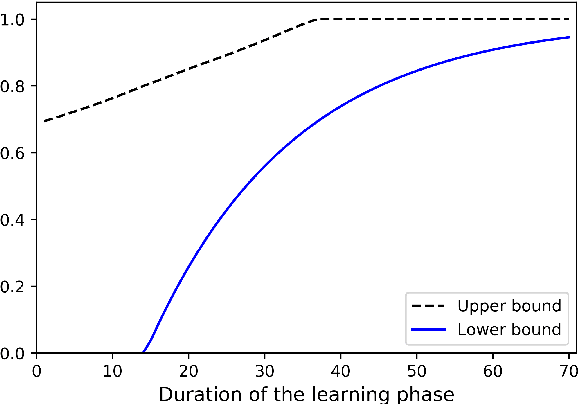
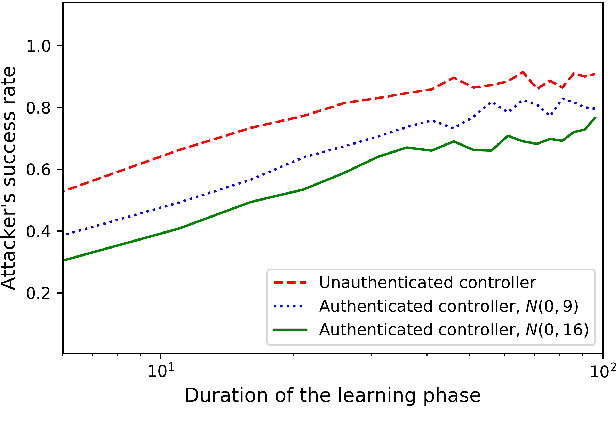
The problem of attacking and authenticating cyber-physical systems is considered. This paper concentrates on the case of a scalar, discrete-time, time-invariant, linear plant under an attack which can override the sensor and the controller signals. Prior works assumed the system was known to all parties and developed watermark-based methods. In contrast, in this paper the attacker needs to learn the open-loop gain in order to carry out a successful attack. A class of two-phase attacks are considered: during an exploration phase, the attacker passively eavesdrops and learns the plant dynamics, followed by an exploitation phase, during which the attacker hijacks the input to the plant and replaces the input to the controller with a carefully crafted fictitious sensor reading with the aim of destabilizing the plant without being detected by the controller. For an authentication test that examines the variance over a time window, tools from information theory and statistics are utilized to derive bounds on the detection and deception probabilities with and without a watermark signal, when the attacker uses an arbitrary learning algorithm to estimate the open-loop gain of the plant.