Kamal Youcef-Toumi
In-Situ Fault Detection of Submerged Pump Impellers Using Encapsulated Accelerometers and Machine Learning
Sep 19, 2025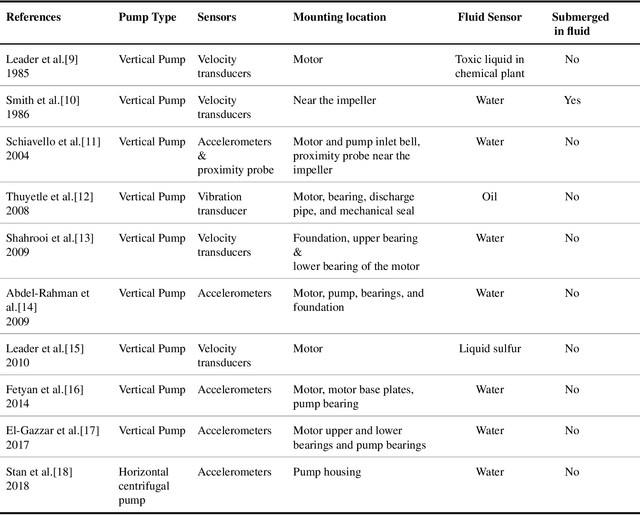
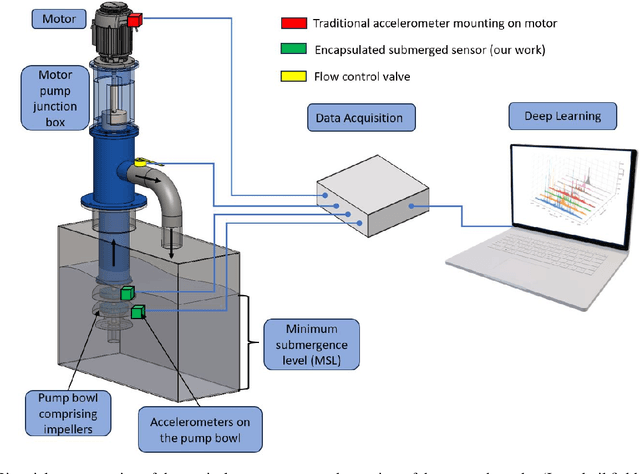
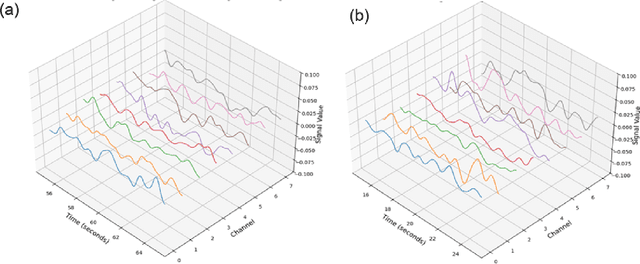

Abstract:Vertical turbine pumps in oil and gas operations rely on motor-mounted accelerometers for condition monitoring. However, these sensors cannot detect faults at submerged impellers exposed to harsh downhole environments. We present the first study deploying encapsulated accelerometers mounted directly on submerged impeller bowls, enabling in-situ vibration monitoring. Using a lab-scale pump setup with 1-meter oil submergence, we collected vibration data under normal and simulated fault conditions. The data were analyzed using a suite of machine learning models -- spanning traditional and deep learning methods -- to evaluate sensor effectiveness. Impeller-mounted sensors achieved 91.3% average accuracy and 0.973 AUC-ROC, outperforming the best non-submerged sensor. Crucially, encapsulation caused no statistically significant performance loss in sensor performance, confirming its viability for oil-submerged environments. While the lab setup used shallow submergence, real-world pump impellers operate up to hundreds of meters underground -- well beyond the range of surface-mounted sensors. This first-of-its-kind in-situ monitoring system demonstrates that impeller-mounted sensors -- encapsulated for protection while preserving diagnostic fidelity -- can reliably detect faults in critical submerged pump components. By capturing localized vibration signatures that are undetectable from surface-mounted sensors, this approach enables earlier fault detection, reduces unplanned downtime, and optimizes maintenance for downhole systems in oil and gas operations.
Eye Movement Feature-Guided Signal De-Drifting in Electrooculography Systems
Sep 09, 2025Abstract:Electrooculography (EOG) is widely used for gaze tracking in Human-Robot Collaboration (HRC). However, baseline drift caused by low-frequency noise significantly impacts the accuracy of EOG signals, creating challenges for further sensor fusion. This paper presents an Eye Movement Feature-Guided De-drift (FGD) method for mitigating drift artifacts in EOG signals. The proposed approach leverages active eye-movement feature recognition to reconstruct the feature-extracted EOG baseline and adaptively correct signal drift while preserving the morphological integrity of the EOG waveform. The FGD is evaluated using both simulation data and real-world data, achieving a significant reduction in mean error. The average error is reduced to 0.896{\deg} in simulation, representing a 36.29% decrease, and to 1.033{\deg} in real-world data, corresponding to a 26.53% reduction. Despite additional and unpredictable noise in real-world data, the proposed method consistently outperforms conventional de-drifting techniques, demonstrating its effectiveness in practical applications such as enhancing human performance augmentation.
Relevance-driven Decision Making for Safer and More Efficient Human Robot Collaboration
Sep 21, 2024
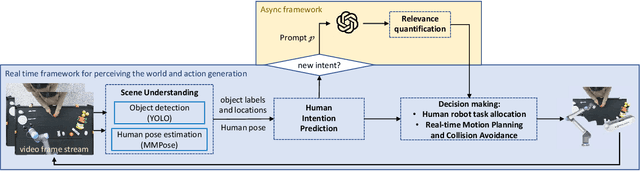
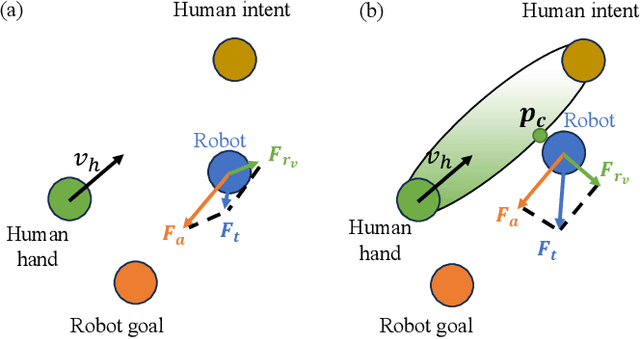
Abstract:Human intelligence possesses the ability to effectively focus on important environmental components, which enhances perception, learning, reasoning, and decision-making. Inspired by this cognitive mechanism, we introduced a novel concept termed relevance for Human-Robot Collaboration (HRC). Relevance is defined as the importance of the objects based on the applicability and pertinence of the objects for the human objective or other factors. In this paper, we further developed a novel two-loop framework integrating real-time and asynchronous processing to quantify relevance and apply relevance for safer and more efficient HRC. The asynchronous loop leverages the world knowledge from an LLM and quantifies relevance, and the real-time loop executes scene understanding, human intent prediction, and decision-making based on relevance. In decision making, we proposed and developed a human robot task allocation method based on relevance and a novel motion generation and collision avoidance methodology considering the prediction of human trajectory. Simulations and experiments show that our methodology for relevance quantification can accurately and robustly predict the human objective and relevance, with an average accuracy of up to 0.90 for objective prediction and up to 0.96 for relevance prediction. Moreover, our motion generation methodology reduces collision cases by 63.76% and collision frames by 44.74% when compared with a state-of-the-art (SOTA) collision avoidance method. Our framework and methodologies, with relevance, guide the robot on how to best assist humans and generate safer and more efficient actions for HRC.
Relevance for Human Robot Collaboration
Sep 12, 2024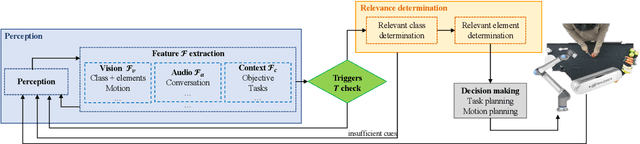
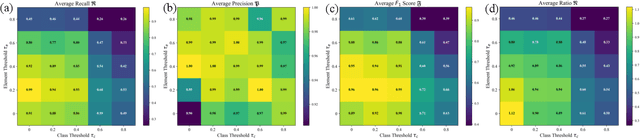
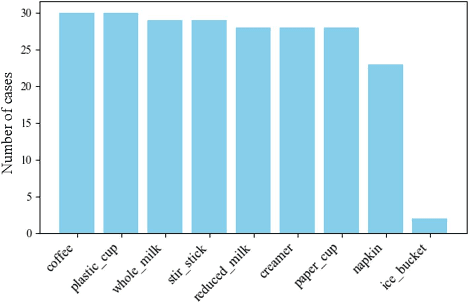

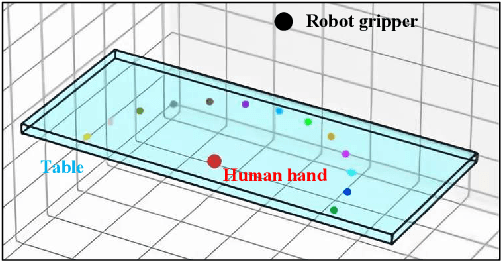
Abstract:Effective human-robot collaboration (HRC) requires the robots to possess human-like intelligence. Inspired by the human's cognitive ability to selectively process and filter elements in complex environments, this paper introduces a novel concept and scene-understanding approach termed `relevance.' It identifies relevant components in a scene. To accurately and efficiently quantify relevance, we developed an event-based framework that selectively triggers relevance determination, along with a probabilistic methodology built on a structured scene representation. Simulation results demonstrate that the relevance framework and methodology accurately predict the relevance of a general HRC setup, achieving a precision of 0.99 and a recall of 0.94. Relevance can be broadly applied to several areas in HRC to improve task planning time by 79.56% compared with pure planning for a cereal task, reduce perception latency by up to 26.53% for an object detector, improve HRC safety by up to 13.50% and reduce the number of inquiries for HRC by 75.36%. A real-world demonstration showcases the relevance framework's ability to intelligently assist humans in everyday tasks.
ISR: Invertible Symbolic Regression
May 10, 2024
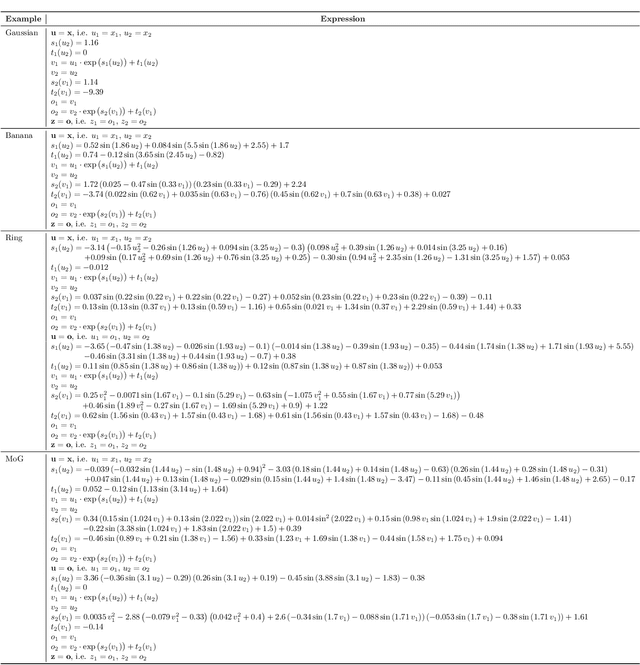

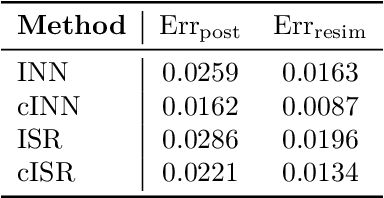
Abstract:We introduce an Invertible Symbolic Regression (ISR) method. It is a machine learning technique that generates analytical relationships between inputs and outputs of a given dataset via invertible maps (or architectures). The proposed ISR method naturally combines the principles of Invertible Neural Networks (INNs) and Equation Learner (EQL), a neural network-based symbolic architecture for function learning. In particular, we transform the affine coupling blocks of INNs into a symbolic framework, resulting in an end-to-end differentiable symbolic invertible architecture that allows for efficient gradient-based learning. The proposed ISR framework also relies on sparsity promoting regularization, allowing the discovery of concise and interpretable invertible expressions. We show that ISR can serve as a (symbolic) normalizing flow for density estimation tasks. Furthermore, we highlight its practical applicability in solving inverse problems, including a benchmark inverse kinematics problem, and notably, a geoacoustic inversion problem in oceanography aimed at inferring posterior distributions of underlying seabed parameters from acoustic signals.
Data-Driven Discovery of PDEs via the Adjoint Method
Jan 30, 2024Abstract:In this work, we present an adjoint-based method for discovering the underlying governing partial differential equations (PDEs) given data. The idea is to consider a parameterized PDE in a general form, and formulate the optimization problem that minimizes the error of PDE solution from data. Using variational calculus, we obtain an evolution equation for the Lagrange multipliers (adjoint equations) allowing us to compute the gradient of the objective function with respect to the parameters of PDEs given data in a straightforward manner. In particular, for a family of parameterized and nonlinear PDEs, we show how the corresponding adjoint equations can be derived. Here, we show that given smooth data set, the proposed adjoint method can recover the true PDE up to machine accuracy. However, in the presence of noise, the accuracy of the adjoint method becomes comparable to the famous PDE Functional Identification of Nonlinear Dynamics method known as PDE-FIND (Rudy et al., 2017). Even though the presented adjoint method relies on forward/backward solvers, it outperforms PDE-FIND for large data sets thanks to the analytic expressions for gradients of the cost function with respect to each PDE parameter.
How Does Perception Affect Safety: New Metrics and Strategy
Dec 12, 2023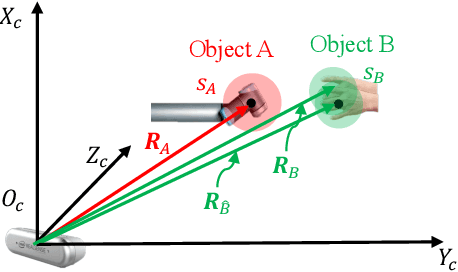
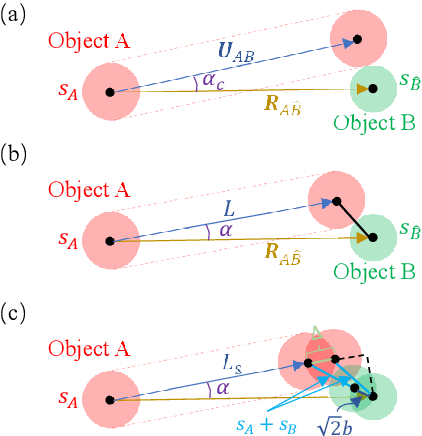
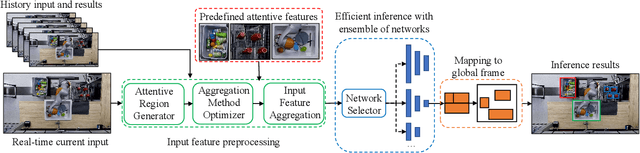
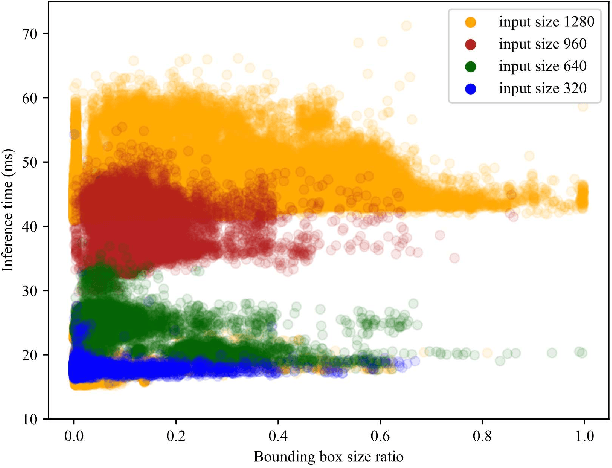
Abstract:Perception serves as a critical component in the functionality of autonomous agents. However, the intricate relationship between perception metrics and robotic metrics remains unclear, leading to ambiguity in the development and fine-tuning of perception algorithms. In this paper, we introduce a methodology for quantifying this relationship, taking into account factors such as detection rate, detection quality, and latency. Furthermore, we introduce two novel metrics for Human-Robot Collaboration safety predicated upon perception metrics: Critical Collision Probability (CCP) and Average Collision Probability (ACP). To validate the utility of these metrics in facilitating algorithm development and tuning, we develop an attentive processing strategy that focuses exclusively on key input features. This approach significantly reduces computational time while preserving a similar level of accuracy. Experimental results indicate that the implementation of this strategy in an object detector leads to a maximum reduction of 30.091% in inference time and 26.534% in total time per frame. Additionally, the strategy lowers the CCP and ACP in a baseline model by 11.252% and 13.501%, respectively. The source code will be made publicly available in the final proof version of the manuscript.
Enhanced Human-Robot Collaboration using Constrained Probabilistic Human-Motion Prediction
Oct 05, 2023Abstract:Human motion prediction is an essential step for efficient and safe human-robot collaboration. Current methods either purely rely on representing the human joints in some form of neural network-based architecture or use regression models offline to fit hyper-parameters in the hope of capturing a model encompassing human motion. While these methods provide good initial results, they are missing out on leveraging well-studied human body kinematic models as well as body and scene constraints which can help boost the efficacy of these prediction frameworks while also explicitly avoiding implausible human joint configurations. We propose a novel human motion prediction framework that incorporates human joint constraints and scene constraints in a Gaussian Process Regression (GPR) model to predict human motion over a set time horizon. This formulation is combined with an online context-aware constraints model to leverage task-dependent motions. It is tested on a human arm kinematic model and implemented on a human-robot collaborative setup with a UR5 robot arm to demonstrate the real-time capability of our approach. Simulations were also performed on datasets like HA4M and ANDY. The simulation and experimental results demonstrate considerable improvements in a Gaussian Process framework when these constraints are explicitly considered.
MESSY Estimation: Maximum-Entropy based Stochastic and Symbolic densitY Estimation
Jun 07, 2023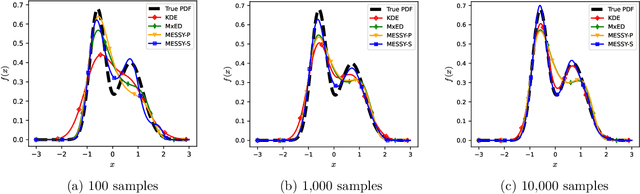
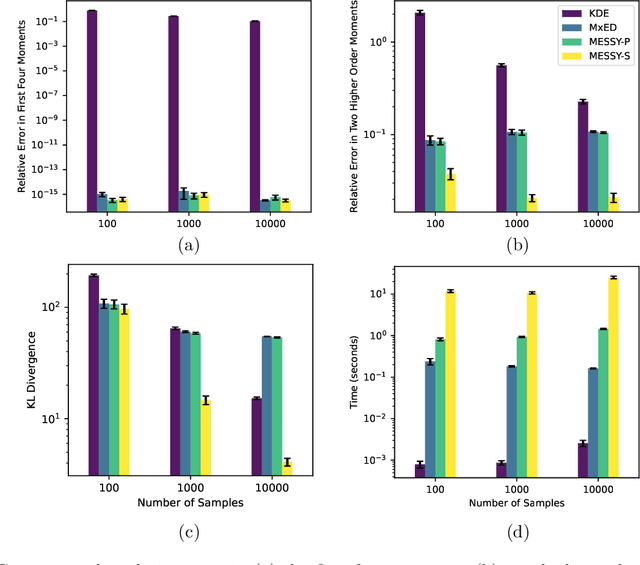
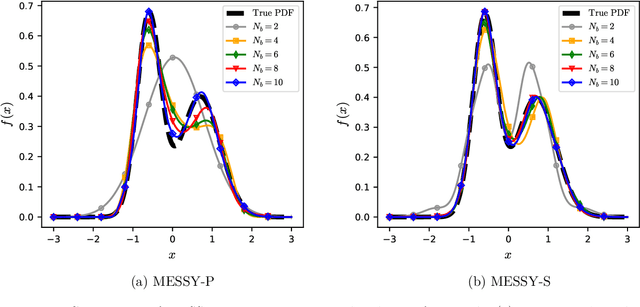
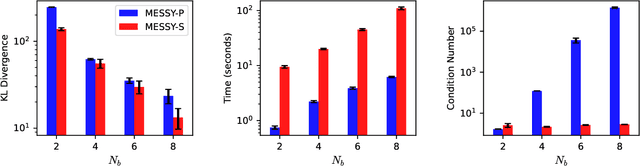
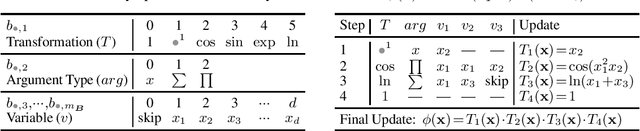
Abstract:We introduce MESSY estimation, a Maximum-Entropy based Stochastic and Symbolic densitY estimation method. The proposed approach recovers probability density functions symbolically from samples using moments of a Gradient flow in which the ansatz serves as the driving force. In particular, we construct a gradient-based drift-diffusion process that connects samples of the unknown distribution function to a guess symbolic expression. We then show that when the guess distribution has the maximum entropy form, the parameters of this distribution can be found efficiently by solving a linear system of equations constructed using the moments of the provided samples. Furthermore, we use Symbolic regression to explore the space of smooth functions and find optimal basis functions for the exponent of the maximum entropy functional leading to good conditioning. The cost of the proposed method in each iteration of the random search is linear with the number of samples and quadratic with the number of basis functions. We validate the proposed MESSY estimation method against other benchmark methods for the case of a bi-modal and a discontinuous density, as well as a density at the limit of physical realizability. We find that the addition of a symbolic search for basis functions improves the accuracy of the estimation at a reasonable additional computational cost. Our results suggest that the proposed method outperforms existing density recovery methods in the limit of a small to moderate number of samples by providing a low-bias and tractable symbolic description of the unknown density at a reasonable computational cost.
GSR: A Generalized Symbolic Regression Approach
May 31, 2022

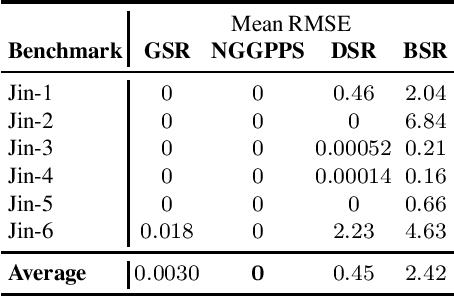
Abstract:Identifying the mathematical relationships that best describe a dataset remains a very challenging problem in machine learning, and is known as Symbolic Regression (SR). In contrast to neural networks which are often treated as black boxes, SR attempts to gain insight into the underlying relationships between the independent variables and the target variable of a given dataset by assembling analytical functions. In this paper, we present GSR, a Generalized Symbolic Regression approach, by modifying the conventional SR optimization problem formulation, while keeping the main SR objective intact. In GSR, we infer mathematical relationships between the independent variables and some transformation of the target variable. We constrain our search space to a weighted sum of basis functions, and propose a genetic programming approach with a matrix-based encoding scheme. We show that our GSR method outperforms several state-of-the-art methods on the well-known SR benchmark problem sets. Finally, we highlight the strengths of GSR by introducing SymSet, a new SR benchmark set which is more challenging relative to the existing benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge