ISR: Invertible Symbolic Regression

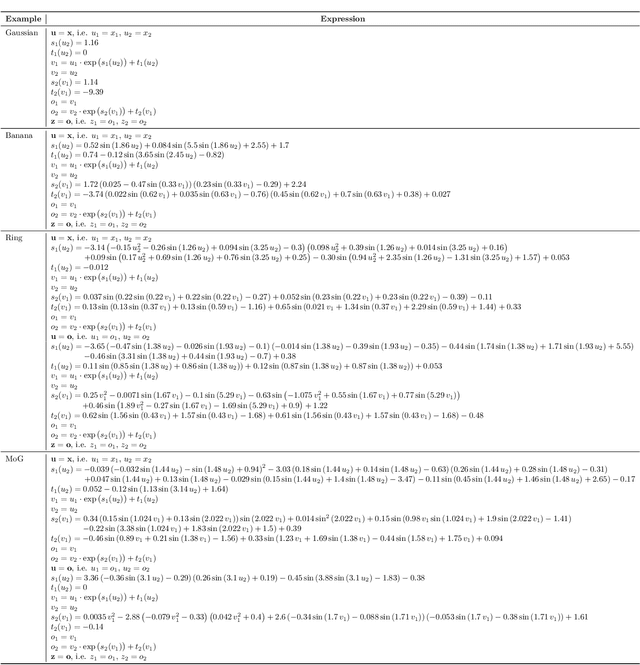
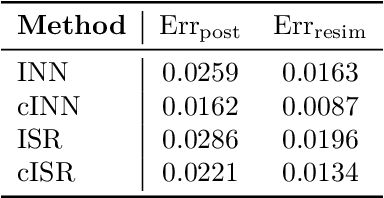
We introduce an Invertible Symbolic Regression (ISR) method. It is a machine learning technique that generates analytical relationships between inputs and outputs of a given dataset via invertible maps (or architectures). The proposed ISR method naturally combines the principles of Invertible Neural Networks (INNs) and Equation Learner (EQL), a neural network-based symbolic architecture for function learning. In particular, we transform the affine coupling blocks of INNs into a symbolic framework, resulting in an end-to-end differentiable symbolic invertible architecture that allows for efficient gradient-based learning. The proposed ISR framework also relies on sparsity promoting regularization, allowing the discovery of concise and interpretable invertible expressions. We show that ISR can serve as a (symbolic) normalizing flow for density estimation tasks. Furthermore, we highlight its practical applicability in solving inverse problems, including a benchmark inverse kinematics problem, and notably, a geoacoustic inversion problem in oceanography aimed at inferring posterior distributions of underlying seabed parameters from acoustic signals.

Data-Driven Discovery of PDEs via the Adjoint Method

In this work, we present an adjoint-based method for discovering the underlying governing partial differential equations (PDEs) given data. The idea is to consider a parameterized PDE in a general form, and formulate the optimization problem that minimizes the error of PDE solution from data. Using variational calculus, we obtain an evolution equation for the Lagrange multipliers (adjoint equations) allowing us to compute the gradient of the objective function with respect to the parameters of PDEs given data in a straightforward manner. In particular, for a family of parameterized and nonlinear PDEs, we show how the corresponding adjoint equations can be derived. Here, we show that given smooth data set, the proposed adjoint method can recover the true PDE up to machine accuracy. However, in the presence of noise, the accuracy of the adjoint method becomes comparable to the famous PDE Functional Identification of Nonlinear Dynamics method known as PDE-FIND (Rudy et al., 2017). Even though the presented adjoint method relies on forward/backward solvers, it outperforms PDE-FIND for large data sets thanks to the analytic expressions for gradients of the cost function with respect to each PDE parameter.

Enhanced Human-Robot Collaboration using Constrained Probabilistic Human-Motion Prediction

Human motion prediction is an essential step for efficient and safe human-robot collaboration. Current methods either purely rely on representing the human joints in some form of neural network-based architecture or use regression models offline to fit hyper-parameters in the hope of capturing a model encompassing human motion. While these methods provide good initial results, they are missing out on leveraging well-studied human body kinematic models as well as body and scene constraints which can help boost the efficacy of these prediction frameworks while also explicitly avoiding implausible human joint configurations. We propose a novel human motion prediction framework that incorporates human joint constraints and scene constraints in a Gaussian Process Regression (GPR) model to predict human motion over a set time horizon. This formulation is combined with an online context-aware constraints model to leverage task-dependent motions. It is tested on a human arm kinematic model and implemented on a human-robot collaborative setup with a UR5 robot arm to demonstrate the real-time capability of our approach. Simulations were also performed on datasets like HA4M and ANDY. The simulation and experimental results demonstrate considerable improvements in a Gaussian Process framework when these constraints are explicitly considered.

MESSY Estimation: Maximum-Entropy based Stochastic and Symbolic densitY Estimation

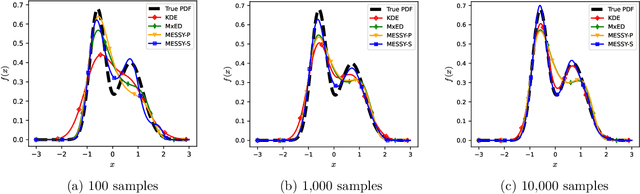
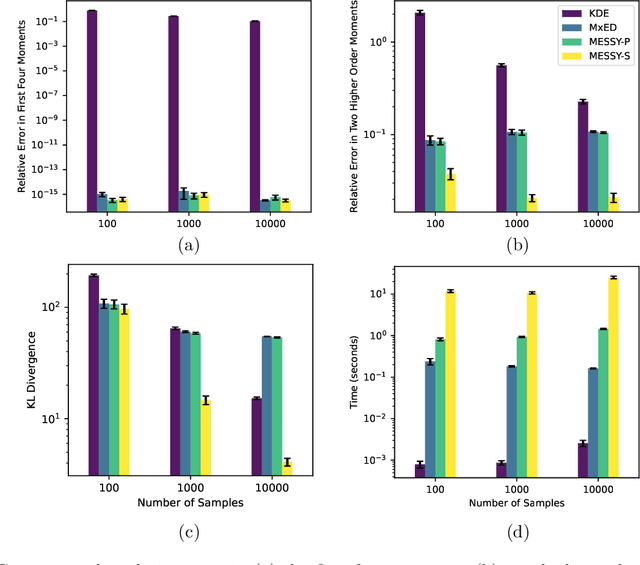
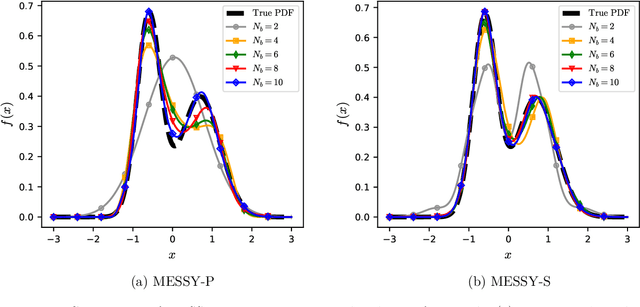
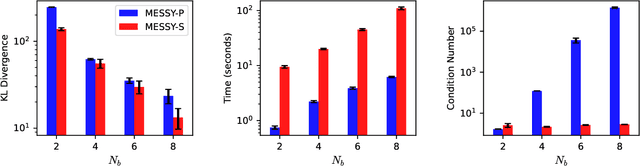
We introduce MESSY estimation, a Maximum-Entropy based Stochastic and Symbolic densitY estimation method. The proposed approach recovers probability density functions symbolically from samples using moments of a Gradient flow in which the ansatz serves as the driving force. In particular, we construct a gradient-based drift-diffusion process that connects samples of the unknown distribution function to a guess symbolic expression. We then show that when the guess distribution has the maximum entropy form, the parameters of this distribution can be found efficiently by solving a linear system of equations constructed using the moments of the provided samples. Furthermore, we use Symbolic regression to explore the space of smooth functions and find optimal basis functions for the exponent of the maximum entropy functional leading to good conditioning. The cost of the proposed method in each iteration of the random search is linear with the number of samples and quadratic with the number of basis functions. We validate the proposed MESSY estimation method against other benchmark methods for the case of a bi-modal and a discontinuous density, as well as a density at the limit of physical realizability. We find that the addition of a symbolic search for basis functions improves the accuracy of the estimation at a reasonable additional computational cost. Our results suggest that the proposed method outperforms existing density recovery methods in the limit of a small to moderate number of samples by providing a low-bias and tractable symbolic description of the unknown density at a reasonable computational cost.

GSR: A Generalized Symbolic Regression Approach

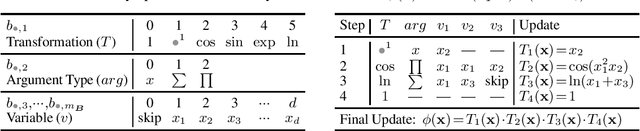
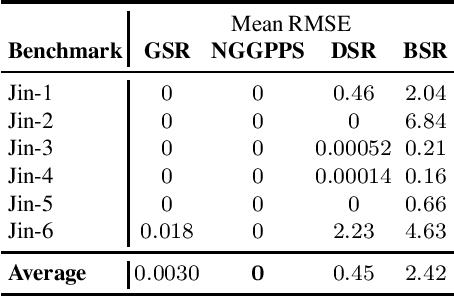
Identifying the mathematical relationships that best describe a dataset remains a very challenging problem in machine learning, and is known as Symbolic Regression (SR). In contrast to neural networks which are often treated as black boxes, SR attempts to gain insight into the underlying relationships between the independent variables and the target variable of a given dataset by assembling analytical functions. In this paper, we present GSR, a Generalized Symbolic Regression approach, by modifying the conventional SR optimization problem formulation, while keeping the main SR objective intact. In GSR, we infer mathematical relationships between the independent variables and some transformation of the target variable. We constrain our search space to a weighted sum of basis functions, and propose a genetic programming approach with a matrix-based encoding scheme. We show that our GSR method outperforms several state-of-the-art methods on the well-known SR benchmark problem sets. Finally, we highlight the strengths of GSR by introducing SymSet, a new SR benchmark set which is more challenging relative to the existing benchmarks.

Improving Regression Uncertainty Estimation Under Statistical Change

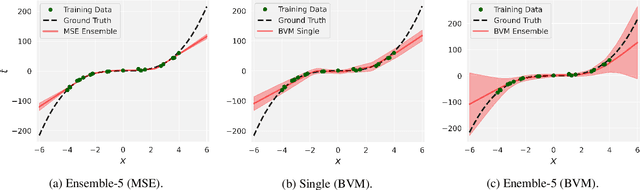
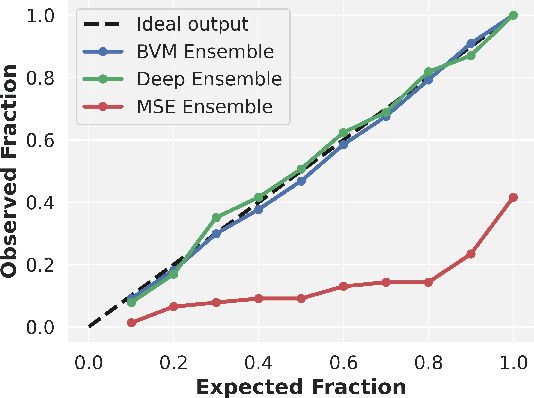
While deep neural networks are highly performant and successful in a wide range of real-world problems, estimating their predictive uncertainty remains a challenging task. To address this challenge, we propose and implement a loss function for regression uncertainty estimation based on the Bayesian Validation Metric (BVM) framework while using ensemble learning. A series of experiments on in-distribution data show that the proposed method is competitive with existing state-of-the-art methods. In addition, experiments on out-of-distribution data show that the proposed method is robust to statistical change and exhibits superior predictive capability.