Collision-based Dynamics for Multi-Marginal Optimal Transport

Inspired by the Boltzmann kinetics, we propose a collision-based dynamics with a Monte Carlo solution algorithm that approximates the solution of the multi-marginal optimal transport problem via randomized pairwise swapping of sample indices. The computational complexity and memory usage of the proposed method scale linearly with the number of samples, making it highly attractive for high-dimensional settings. In several examples, we demonstrate the efficiency of the proposed method compared to the state-of-the-art methods.

Optimal Transportation by Orthogonal Coupling Dynamics

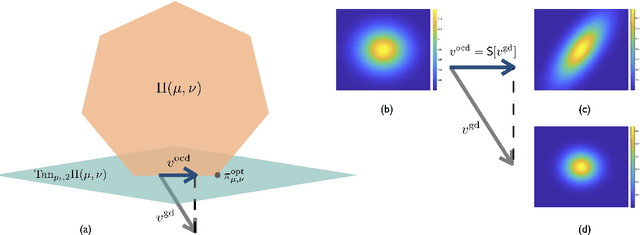
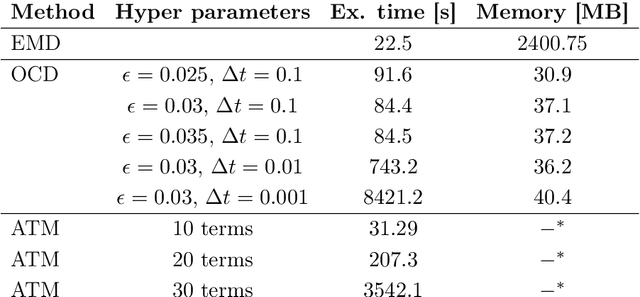
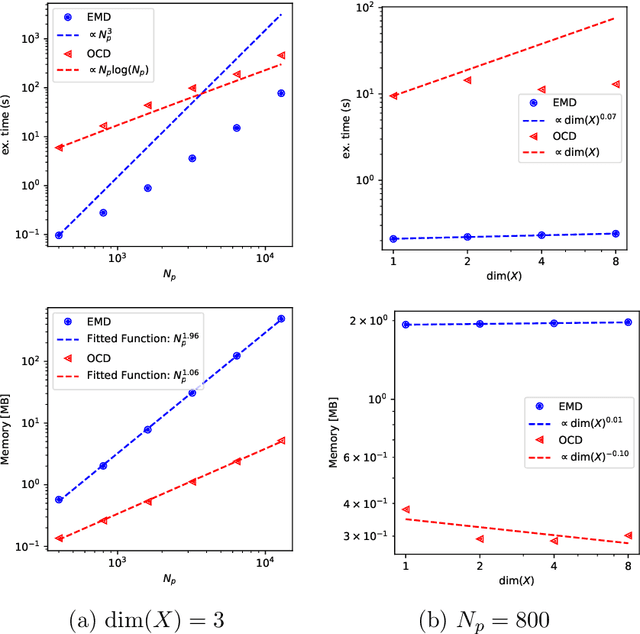
Many numerical algorithms and learning tasks rest on solution of the Monge-Kantorovich problem and corresponding Wasserstein distances. While the natural approach is to treat the problem as an infinite-dimensional linear programming, such a methodology severely limits the computational performance due to the polynomial scaling with respect to the sample size along with intensive memory requirements. We propose a novel alternative framework to address the Monge-Kantorovich problem based on a projection type gradient descent scheme. The micro-dynamics is built on the notion of the conditional expectation, where the connection with the opinion dynamics is explored and leveraged to build compact numerical schemes. We demonstrate that the devised dynamics recovers random maps with favourable computational performance. Along with the theoretical insight, the provided dynamics paves the way for innovative approaches to construct numerical schemes for computing optimal transport maps as well as Wasserstein distances.

ISR: Invertible Symbolic Regression

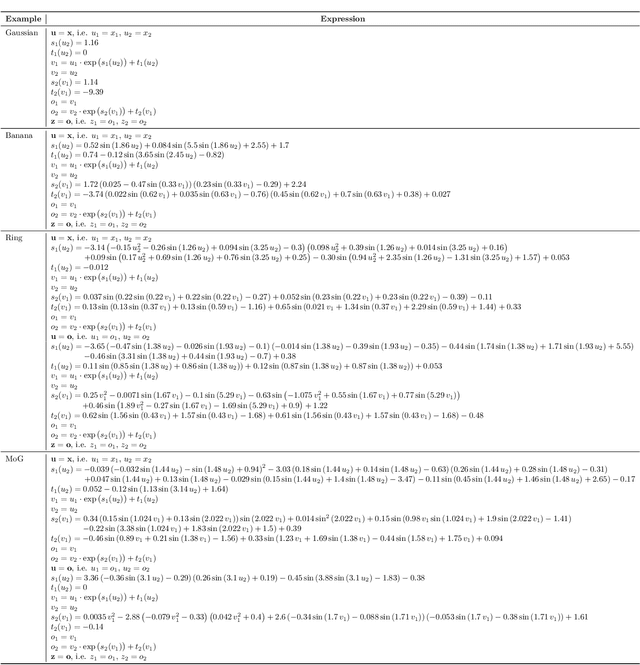
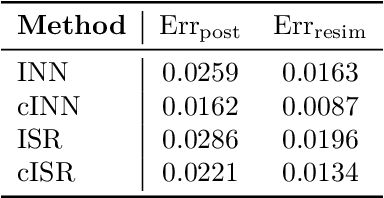
We introduce an Invertible Symbolic Regression (ISR) method. It is a machine learning technique that generates analytical relationships between inputs and outputs of a given dataset via invertible maps (or architectures). The proposed ISR method naturally combines the principles of Invertible Neural Networks (INNs) and Equation Learner (EQL), a neural network-based symbolic architecture for function learning. In particular, we transform the affine coupling blocks of INNs into a symbolic framework, resulting in an end-to-end differentiable symbolic invertible architecture that allows for efficient gradient-based learning. The proposed ISR framework also relies on sparsity promoting regularization, allowing the discovery of concise and interpretable invertible expressions. We show that ISR can serve as a (symbolic) normalizing flow for density estimation tasks. Furthermore, we highlight its practical applicability in solving inverse problems, including a benchmark inverse kinematics problem, and notably, a geoacoustic inversion problem in oceanography aimed at inferring posterior distributions of underlying seabed parameters from acoustic signals.

Data-Driven Discovery of PDEs via the Adjoint Method

In this work, we present an adjoint-based method for discovering the underlying governing partial differential equations (PDEs) given data. The idea is to consider a parameterized PDE in a general form, and formulate the optimization problem that minimizes the error of PDE solution from data. Using variational calculus, we obtain an evolution equation for the Lagrange multipliers (adjoint equations) allowing us to compute the gradient of the objective function with respect to the parameters of PDEs given data in a straightforward manner. In particular, for a family of parameterized and nonlinear PDEs, we show how the corresponding adjoint equations can be derived. Here, we show that given smooth data set, the proposed adjoint method can recover the true PDE up to machine accuracy. However, in the presence of noise, the accuracy of the adjoint method becomes comparable to the famous PDE Functional Identification of Nonlinear Dynamics method known as PDE-FIND (Rudy et al., 2017). Even though the presented adjoint method relies on forward/backward solvers, it outperforms PDE-FIND for large data sets thanks to the analytic expressions for gradients of the cost function with respect to each PDE parameter.

Gaussian Process Regression for Maximum Entropy Distribution

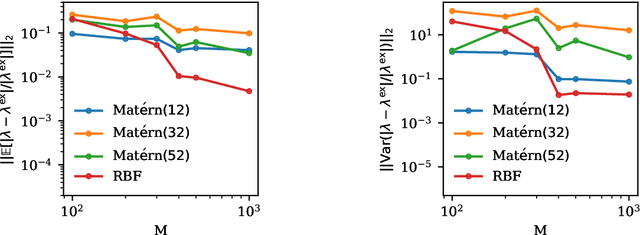
Maximum-Entropy Distributions offer an attractive family of probability densities suitable for moment closure problems. Yet finding the Lagrange multipliers which parametrize these distributions, turns out to be a computational bottleneck for practical closure settings. Motivated by recent success of Gaussian processes, we investigate the suitability of Gaussian priors to approximate the Lagrange multipliers as a map of a given set of moments. Examining various kernel functions, the hyperparameters are optimized by maximizing the log-likelihood. The performance of the devised data-driven Maximum-Entropy closure is studied for couple of test cases including relaxation of non-equilibrium distributions governed by Bhatnagar-Gross-Krook and Boltzmann kinetic equations.

MESSY Estimation: Maximum-Entropy based Stochastic and Symbolic densitY Estimation

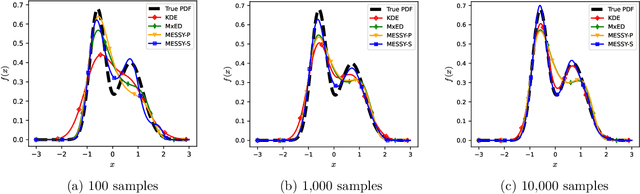
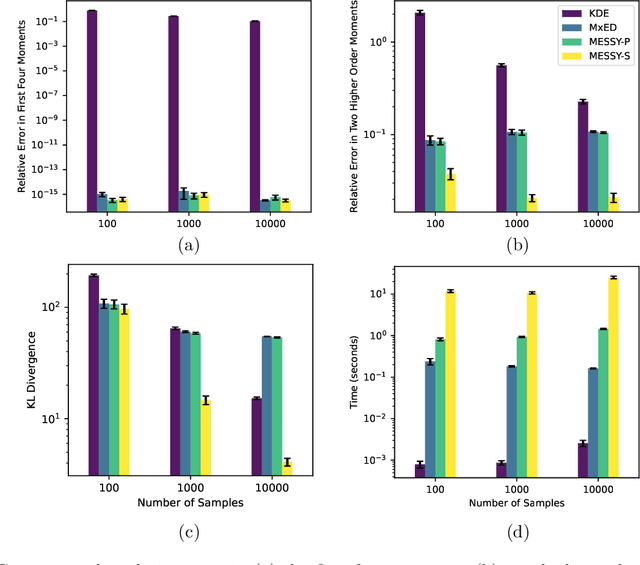
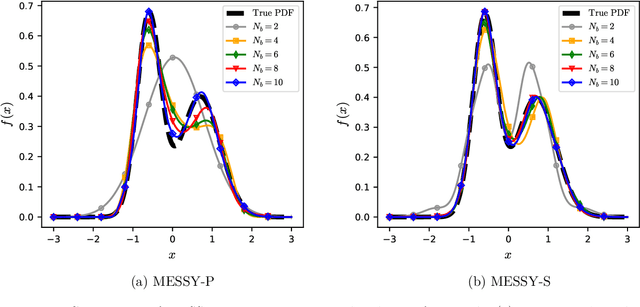
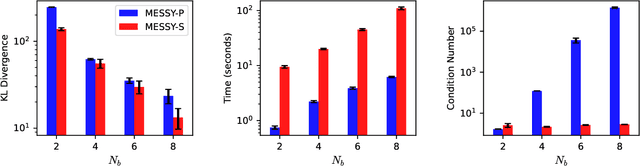
We introduce MESSY estimation, a Maximum-Entropy based Stochastic and Symbolic densitY estimation method. The proposed approach recovers probability density functions symbolically from samples using moments of a Gradient flow in which the ansatz serves as the driving force. In particular, we construct a gradient-based drift-diffusion process that connects samples of the unknown distribution function to a guess symbolic expression. We then show that when the guess distribution has the maximum entropy form, the parameters of this distribution can be found efficiently by solving a linear system of equations constructed using the moments of the provided samples. Furthermore, we use Symbolic regression to explore the space of smooth functions and find optimal basis functions for the exponent of the maximum entropy functional leading to good conditioning. The cost of the proposed method in each iteration of the random search is linear with the number of samples and quadratic with the number of basis functions. We validate the proposed MESSY estimation method against other benchmark methods for the case of a bi-modal and a discontinuous density, as well as a density at the limit of physical realizability. We find that the addition of a symbolic search for basis functions improves the accuracy of the estimation at a reasonable additional computational cost. Our results suggest that the proposed method outperforms existing density recovery methods in the limit of a small to moderate number of samples by providing a low-bias and tractable symbolic description of the unknown density at a reasonable computational cost.