Optimal Transportation by Orthogonal Coupling Dynamics
Paper and Code
Oct 10, 2024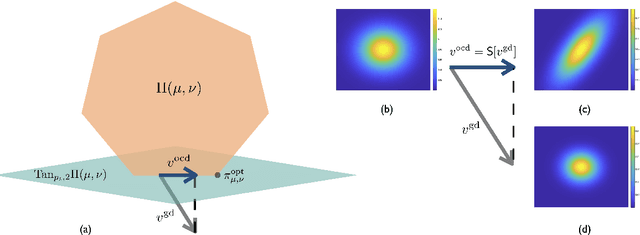
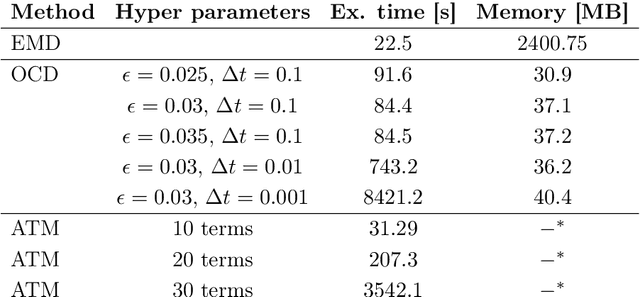
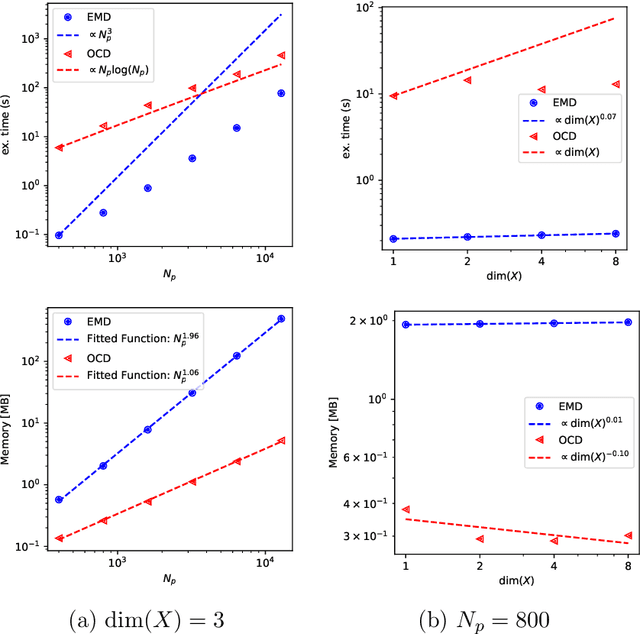

Many numerical algorithms and learning tasks rest on solution of the Monge-Kantorovich problem and corresponding Wasserstein distances. While the natural approach is to treat the problem as an infinite-dimensional linear programming, such a methodology severely limits the computational performance due to the polynomial scaling with respect to the sample size along with intensive memory requirements. We propose a novel alternative framework to address the Monge-Kantorovich problem based on a projection type gradient descent scheme. The micro-dynamics is built on the notion of the conditional expectation, where the connection with the opinion dynamics is explored and leveraged to build compact numerical schemes. We demonstrate that the devised dynamics recovers random maps with favourable computational performance. Along with the theoretical insight, the provided dynamics paves the way for innovative approaches to construct numerical schemes for computing optimal transport maps as well as Wasserstein distances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge