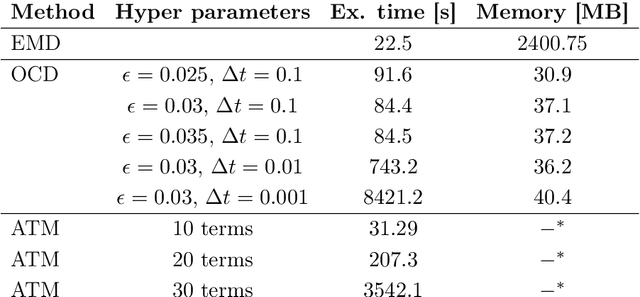
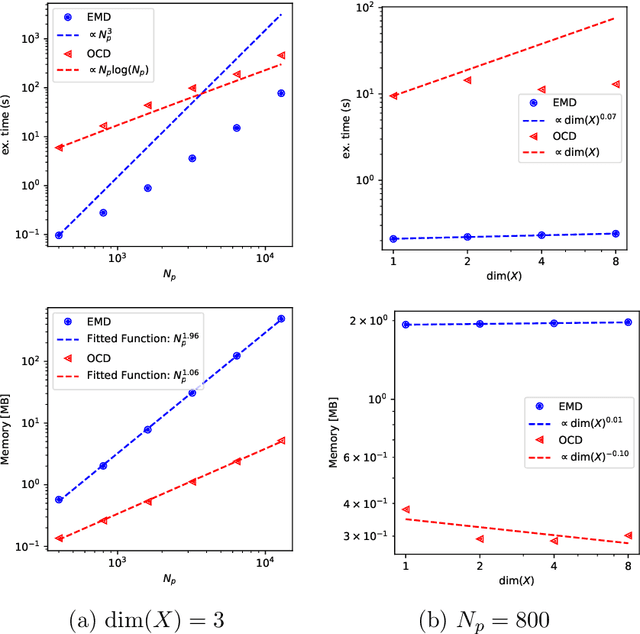
Collision-based Dynamics for Multi-Marginal Optimal Transport

Inspired by the Boltzmann kinetics, we propose a collision-based dynamics with a Monte Carlo solution algorithm that approximates the solution of the multi-marginal optimal transport problem via randomized pairwise swapping of sample indices. The computational complexity and memory usage of the proposed method scale linearly with the number of samples, making it highly attractive for high-dimensional settings. In several examples, we demonstrate the efficiency of the proposed method compared to the state-of-the-art methods.

Optimal Transportation by Orthogonal Coupling Dynamics

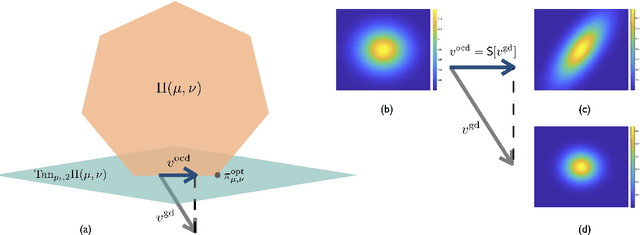
Many numerical algorithms and learning tasks rest on solution of the Monge-Kantorovich problem and corresponding Wasserstein distances. While the natural approach is to treat the problem as an infinite-dimensional linear programming, such a methodology severely limits the computational performance due to the polynomial scaling with respect to the sample size along with intensive memory requirements. We propose a novel alternative framework to address the Monge-Kantorovich problem based on a projection type gradient descent scheme. The micro-dynamics is built on the notion of the conditional expectation, where the connection with the opinion dynamics is explored and leveraged to build compact numerical schemes. We demonstrate that the devised dynamics recovers random maps with favourable computational performance. Along with the theoretical insight, the provided dynamics paves the way for innovative approaches to construct numerical schemes for computing optimal transport maps as well as Wasserstein distances.