Inferential Moments of Uncertain Multivariable Systems

This article offers a new paradigm for analyzing the behavior of uncertain multivariable systems using a set of quantities we call \emph{inferential moments}. Marginalization is an uncertainty quantification process that averages conditional probabilities to quantify the \emph{expected value} of a probability of interest. Inferential moments are higher order conditional probability moments that describe how a distribution is expected to respond to new information. Of particular interest in this article is the \emph{inferential deviation}, which is the expected fluctuation of the probability of one variable in response to an inferential update of another. We find a power series expansion of the Mutual Information in terms of inferential moments, which implies that inferential moment logic may be useful for tasks typically performed with information theoretic tools. We explore this in two applications that analyze the inferential deviations of a Bayesian Network to improve situational awareness and decision-making. We implement a simple greedy algorithm for optimal sensor tasking using inferential deviations that generally outperforms a similar greedy Mutual Information algorithm in terms of predictive probabilistic error.

Improving Regression Uncertainty Estimation Under Statistical Change

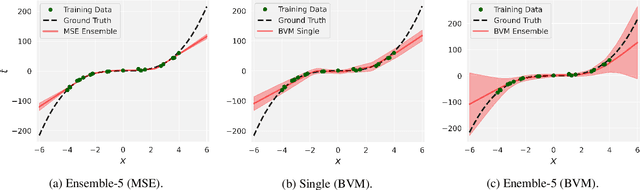
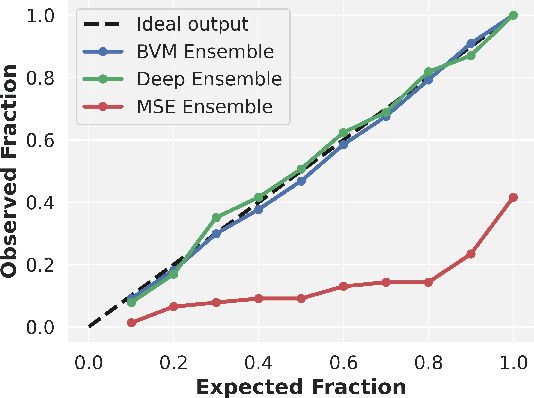
While deep neural networks are highly performant and successful in a wide range of real-world problems, estimating their predictive uncertainty remains a challenging task. To address this challenge, we propose and implement a loss function for regression uncertainty estimation based on the Bayesian Validation Metric (BVM) framework while using ensemble learning. A series of experiments on in-distribution data show that the proposed method is competitive with existing state-of-the-art methods. In addition, experiments on out-of-distribution data show that the proposed method is robust to statistical change and exhibits superior predictive capability.

The Design of Mutual Information as a Global Correlation Quantifier

We design a functional that is capable of quantifying the amount of global correlations encoded in a given probability distribution $\rho$, by imposing what we call the \textit{Principle of Constant Correlations} (PCC) and using eliminative induction. The residual functional after eliminative induction is the mutual information (MI) and therefore the MI is designed to quantify the amount of global correlations encoded in $\rho$. The MI is the unique functional capable of determining whether a certain class of inferential transformations, $\rho\xrightarrow{*}\rho'$, preserve, destroy or create correlations. Further, Our design derivation allows us to improve the notion and efficacy of statistical sufficiency by expressing it in terms of a normalized MI that represents the percentage in which a statistic or transformation is a sufficient.