GSR: A Generalized Symbolic Regression Approach

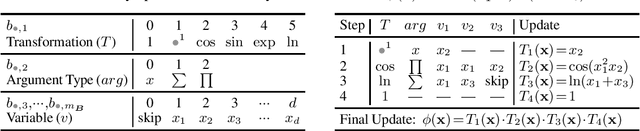
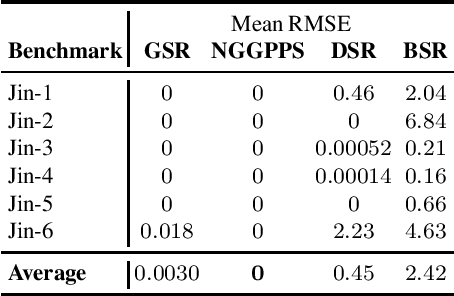
Identifying the mathematical relationships that best describe a dataset remains a very challenging problem in machine learning, and is known as Symbolic Regression (SR). In contrast to neural networks which are often treated as black boxes, SR attempts to gain insight into the underlying relationships between the independent variables and the target variable of a given dataset by assembling analytical functions. In this paper, we present GSR, a Generalized Symbolic Regression approach, by modifying the conventional SR optimization problem formulation, while keeping the main SR objective intact. In GSR, we infer mathematical relationships between the independent variables and some transformation of the target variable. We constrain our search space to a weighted sum of basis functions, and propose a genetic programming approach with a matrix-based encoding scheme. We show that our GSR method outperforms several state-of-the-art methods on the well-known SR benchmark problem sets. Finally, we highlight the strengths of GSR by introducing SymSet, a new SR benchmark set which is more challenging relative to the existing benchmarks.

Fast and High-Quality Blind Multi-Spectral Image Pansharpening

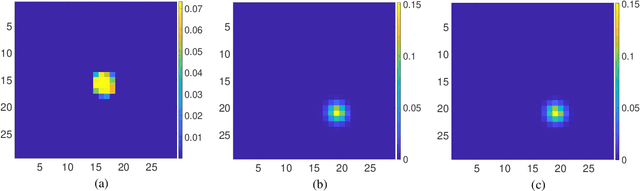
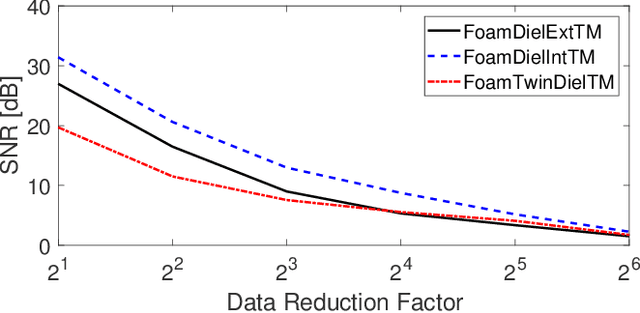
Blind pansharpening addresses the problem of generating a high spatial-resolution multi-spectral (HRMS) image given a low spatial-resolution multi-spectral (LRMS) image with the guidance of its associated spatially misaligned high spatial-resolution panchromatic (PAN) image without parametric side information. In this paper, we propose a fast approach to blind pansharpening and achieve state-of-the-art image reconstruction quality. Typical blind pansharpening algorithms are often computationally intensive since the blur kernel and the target HRMS image are often computed using iterative solvers and in an alternating fashion. To achieve fast blind pansharpening, we decouple the solution of the blur kernel and of the HRMS image. First, we estimate the blur kernel by computing the kernel coefficients with minimum total generalized variation that blur a downsampled version of the PAN image to approximate a linear combination of the LRMS image channels. Then, we estimate each channel of the HRMS image using local Laplacian prior to regularize the relationship between each HRMS channel and the PAN image. Solving the HRMS image is accelerated by both parallelizing across the channels and by fast numerical algorithms for each channel. Due to the fast scheme and the powerful priors we used on the blur kernel coefficients (total generalized variation) and on the cross-channel relationship (local Laplacian prior), numerical experiments demonstrate that our algorithm outperforms state-of-the-art model-based counterparts in terms of both computational time and reconstruction quality of the HRMS images.

Sparse Blind Deconvolution for Distributed Radar Autofocus Imaging

A common problem that arises in radar imaging systems, especially those mounted on mobile platforms, is antenna position ambiguity. Approaches to resolve this ambiguity and correct position errors are generally known as radar autofocus. Common techniques that attempt to resolve the antenna ambiguity generally assume an unknown gain and phase error afflicting the radar measurements. However, ensuring identifiability and tractability of the unknown error imposes strict restrictions on the allowable antenna perturbations. Furthermore, these techniques are often not applicable in near-field imaging, where mapping the position ambiguity to phase errors breaks down. In this paper, we propose an alternate formulation where the position error of each antenna is mapped to a spatial shift operator in the image-domain. Thus, the radar autofocus problem becomes a multichannel blind deconvolution problem, in which the radar measurements correspond to observations of a static radar image that is convolved with the spatial shift kernel associated with each antenna. To solve the reformulated problem, we also develop a block coordinate descent framework that leverages the sparsity and piece-wise smoothness of the radar scene, as well as the one-sparse property of the two dimensional shift kernels. We evaluate the performance of our approach using both simulated and experimental radar measurements, and demonstrate its superior performance compared to state-of-the-art methods.

Accelerated Image Reconstruction for Nonlinear Diffractive Imaging

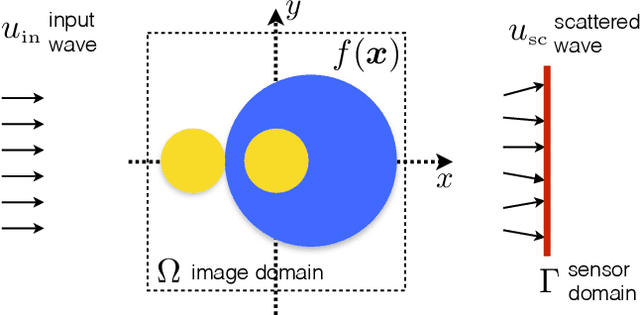
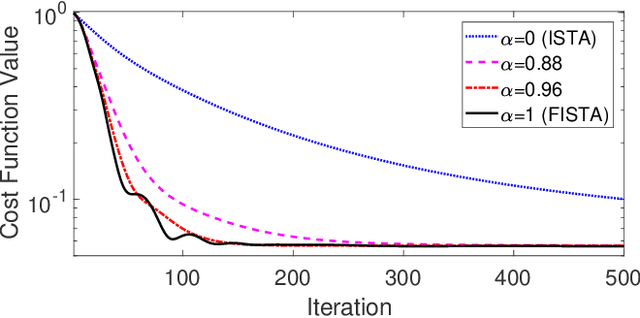
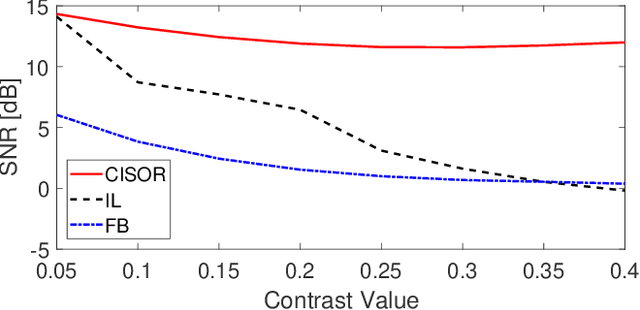
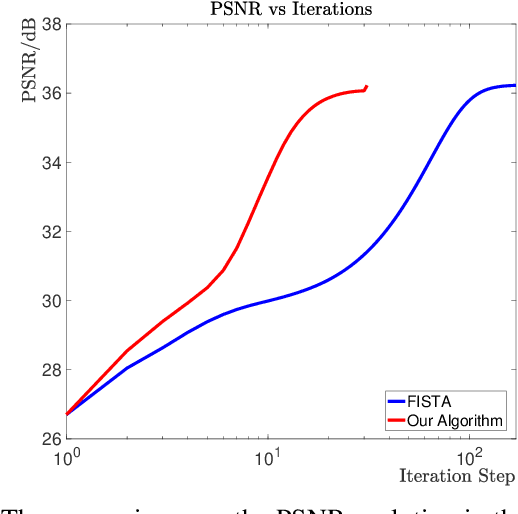
The problem of reconstructing an object from the measurements of the light it scatters is common in numerous imaging applications. While the most popular formulations of the problem are based on linearizing the object-light relationship, there is an increased interest in considering nonlinear formulations that can account for multiple light scattering. In this paper, we propose an image reconstruction method, called CISOR, for nonlinear diffractive imaging, based on a nonconvex optimization formulation with total variation (TV) regularization. The nonconvex solver used in CISOR is our new variant of fast iterative shrinkage/thresholding algorithm (FISTA). We provide fast and memory-efficient implementation of the new FISTA variant and prove that it reliably converges for our nonconvex optimization problem. In addition, we systematically compare our method with other state-of-the-art methods on simulated as well as experimentally measured data in both 2D and 3D settings.

Online Convolutional Dictionary Learning for Multimodal Imaging

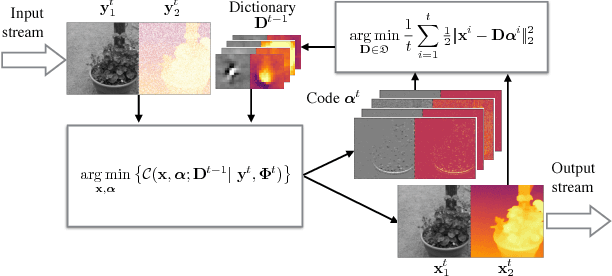
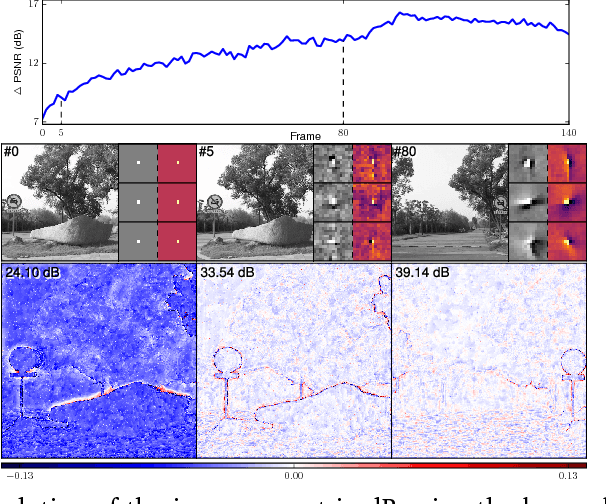
Computational imaging methods that can exploit multiple modalities have the potential to enhance the capabilities of traditional sensing systems. In this paper, we propose a new method that reconstructs multimodal images from their linear measurements by exploiting redundancies across different modalities. Our method combines a convolutional group-sparse representation of images with total variation (TV) regularization for high-quality multimodal imaging. We develop an online algorithm that enables the unsupervised learning of convolutional dictionaries on large-scale datasets that are typical in such applications. We illustrate the benefit of our approach in the context of joint intensity-depth imaging.

SEAGLE: Sparsity-Driven Image Reconstruction under Multiple Scattering

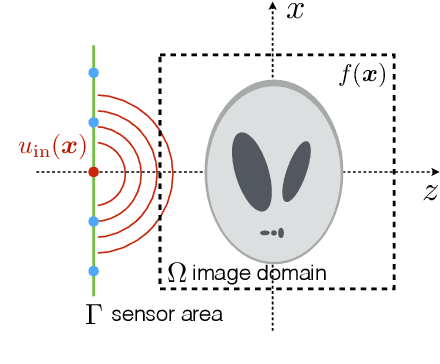
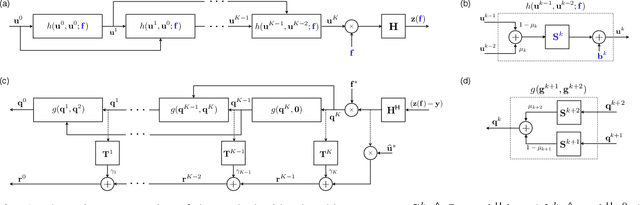
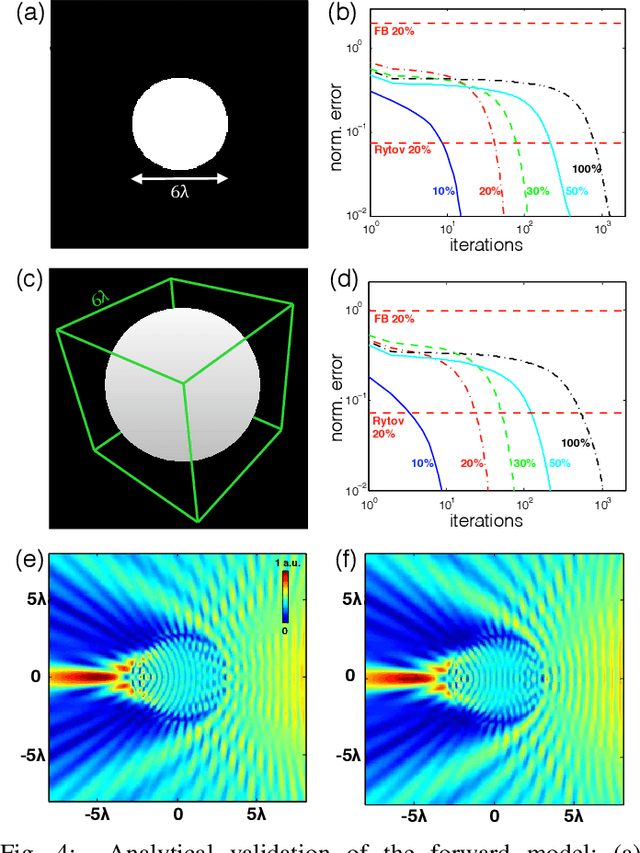
Multiple scattering of an electromagnetic wave as it passes through an object is a fundamental problem that limits the performance of current imaging systems. In this paper, we describe a new technique-called Series Expansion with Accelerated Gradient Descent on Lippmann-Schwinger Equation (SEAGLE)-for robust imaging under multiple scattering based on a combination of a new nonlinear forward model and a total variation (TV) regularizer. The proposed forward model can account for multiple scattering, which makes it advantageous in applications where linear models are inaccurate. Specifically, it corresponds to a series expansion of the scattered wave with an accelerated-gradient method. This expansion guarantees the convergence even for strongly scattering objects. One of our key insights is that it is possible to obtain an explicit formula for computing the gradient of our nonlinear forward model with respect to the unknown object, thus enabling fast image reconstruction with the state-of-the-art fast iterative shrinkage/thresholding algorithm (FISTA). The proposed method is validated on both simulated and experimentally measured data.

Compressive Imaging with Iterative Forward Models

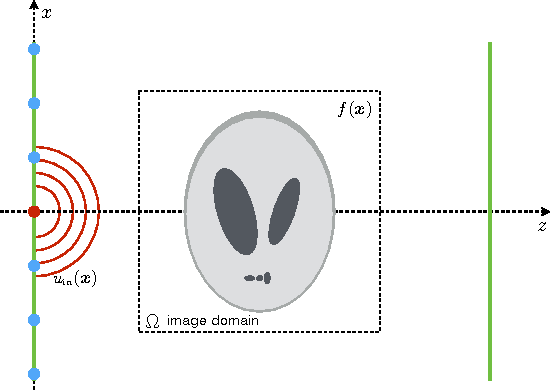
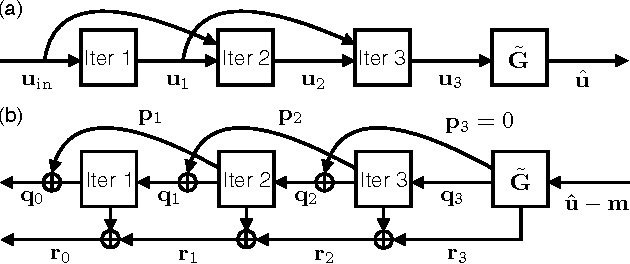
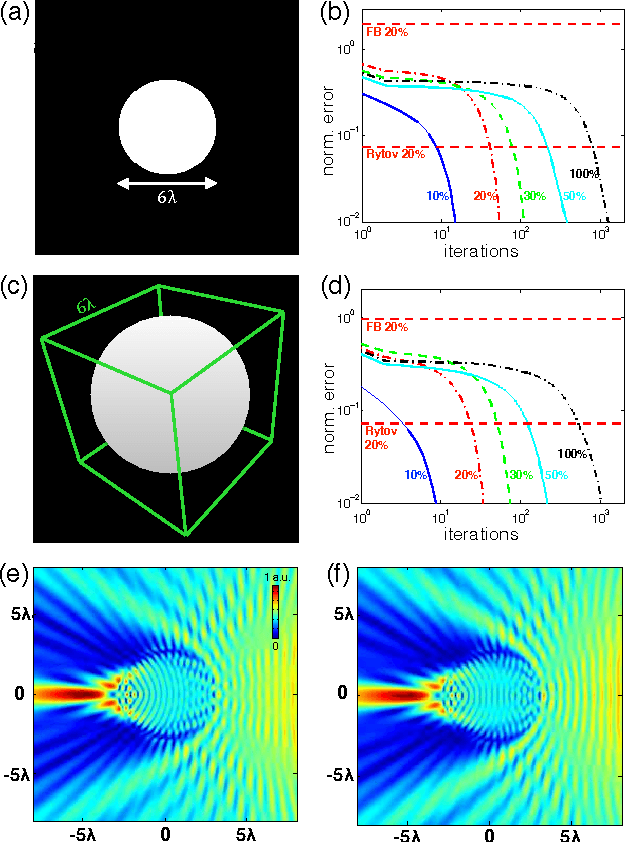
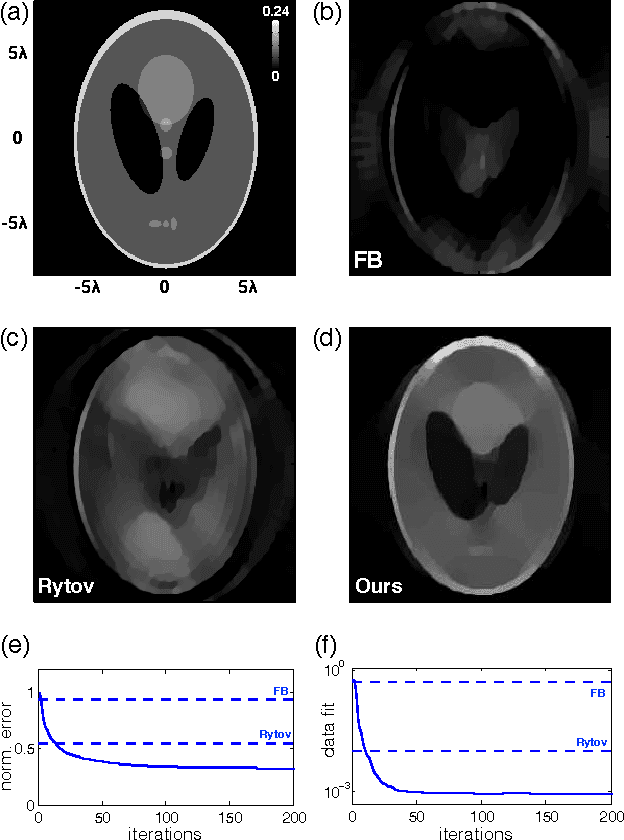
We propose a new compressive imaging method for reconstructing 2D or 3D objects from their scattered wave-field measurements. Our method relies on a novel, nonlinear measurement model that can account for the multiple scattering phenomenon, which makes the method preferable in applications where linear measurement models are inaccurate. We construct the measurement model by expanding the scattered wave-field with an accelerated-gradient method, which is guaranteed to converge and is suitable for large-scale problems. We provide explicit formulas for computing the gradient of our measurement model with respect to the unknown image, which enables image formation with a sparsity- driven numerical optimization algorithm. We validate the method both analytically and with numerical simulations.

A Recursive Born Approach to Nonlinear Inverse Scattering

The Iterative Born Approximation (IBA) is a well-known method for describing waves scattered by semi-transparent objects. In this paper, we present a novel nonlinear inverse scattering method that combines IBA with an edge-preserving total variation (TV) regularizer. The proposed method is obtained by relating iterations of IBA to layers of a feedforward neural network and developing a corresponding error backpropagation algorithm for efficiently estimating the permittivity of the object. Simulations illustrate that, by accounting for multiple scattering, the method successfully recovers the permittivity distribution where the traditional linear inverse scattering fails.