Multiview Sensing With Unknown Permutations: An Optimal Transport Approach

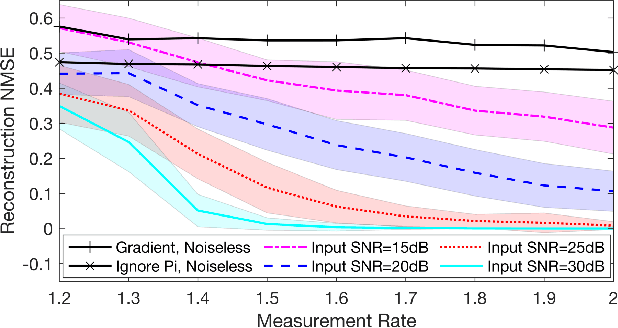
In several applications, including imaging of deformable objects while in motion, simultaneous localization and mapping, and unlabeled sensing, we encounter the problem of recovering a signal that is measured subject to unknown permutations. In this paper we take a fresh look at this problem through the lens of optimal transport (OT). In particular, we recognize that in most practical applications the unknown permutations are not arbitrary but some are more likely to occur than others. We exploit this by introducing a regularization function that promotes the more likely permutations in the solution. We show that, even though the general problem is not convex, an appropriate relaxation of the resulting regularized problem allows us to exploit the well-developed machinery of OT and develop a tractable algorithm.

Two-Dimensional Non-Line-of-Sight Scene Estimation from a Single Edge Occluder

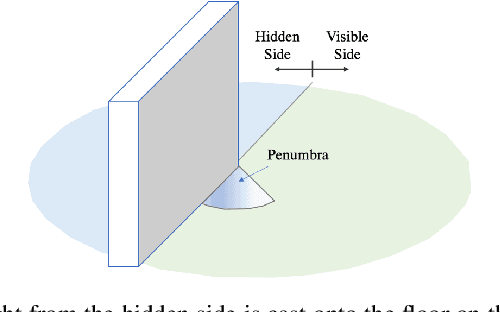
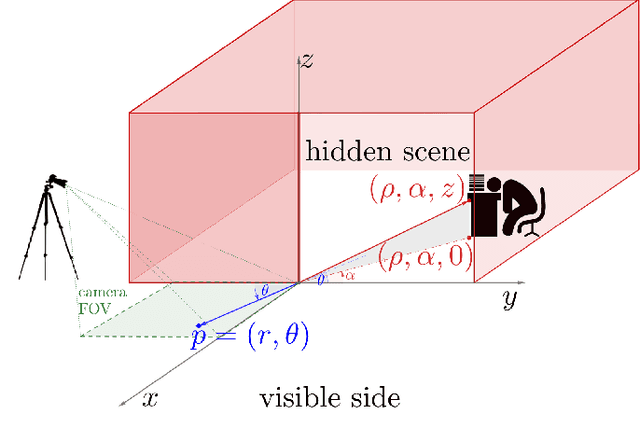
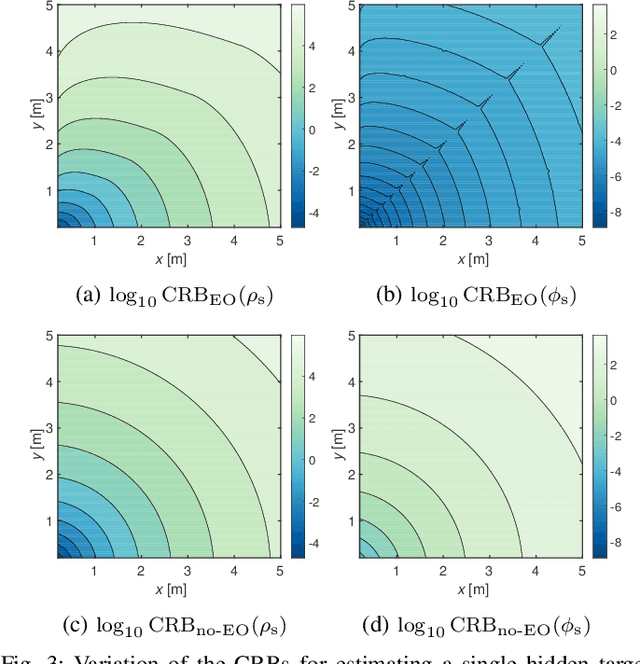
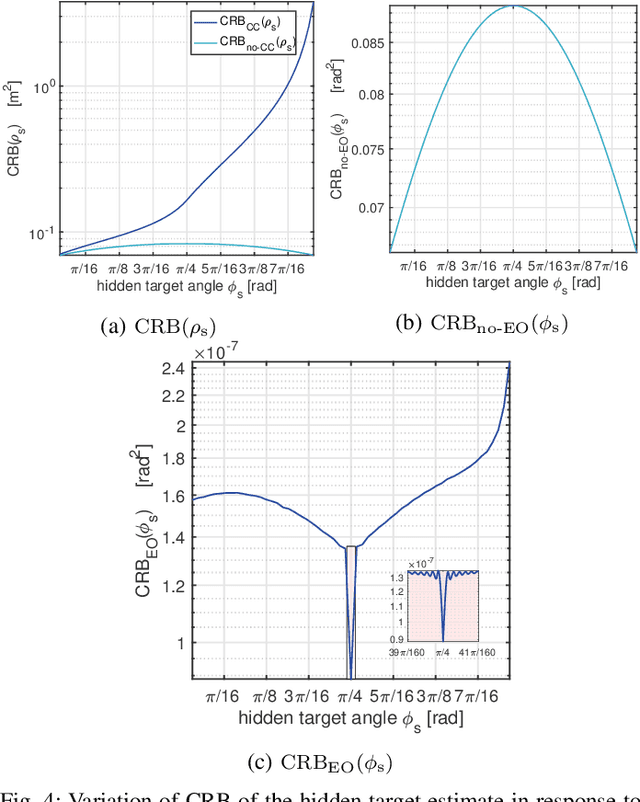
Passive non-line-of-sight imaging methods are often faster and stealthier than their active counterparts, requiring less complex and costly equipment. However, many of these methods exploit motion of an occluder or the hidden scene, or require knowledge or calibration of complicated occluders. The edge of a wall is a known and ubiquitous occluding structure that may be used as an aperture to image the region hidden behind it. Light from around the corner is cast onto the floor forming a fan-like penumbra rather than a sharp shadow. Subtle variations in the penumbra contain a remarkable amount of information about the hidden scene. Previous work has leveraged the vertical nature of the edge to demonstrate 1D (in angle measured around the corner) reconstructions of moving and stationary hidden scenery from as little as a single photograph of the penumbra. In this work, we introduce a second reconstruction dimension: range measured from the edge. We derive a new forward model, accounting for radial falloff, and propose two inversion algorithms to form 2D reconstructions from a single photograph of the penumbra. Performances of both algorithms are demonstrated on experimental data corresponding to several different hidden scene configurations. A Cramer-Rao bound analysis further demonstrates the feasibility (and utility) of the 2D corner camera.

On the modes of convergence of Stochastic Optimistic Mirror Descent for saddle point problems

In this article, we study the convergence of Mirror Descent (MD) and Optimistic Mirror Descent (OMD) for saddle point problems satisfying the notion of coherence as proposed in Mertikopoulos et al. We prove convergence of OMD with exact gradients for coherent saddle point problems, and show that monotone convergence only occurs after some sufficiently large number of iterations. This is in contrast to the claim in Mertikopoulos et al. of monotone convergence of OMD with exact gradients for coherent saddle point problems. Besides highlighting this important subtlety, we note that the almost sure convergence guarantees of MD and OMD with stochastic gradients for strictly coherent saddle point problems that are claimed in Mertikopoulos et al. are not fully justified by their proof. As such, we fill out the missing details in the proof and as a result have only been able to prove convergence with high probability. We would like to note that our analysis relies heavily on the core ideas and proof techniques introduced in Zhou et al. and Mertikopoulos et al., and we only aim to re-state and correct the results in light of what we were able to prove rigorously while filling in the much needed missing details in their proofs.

Accelerated Image Reconstruction for Nonlinear Diffractive Imaging

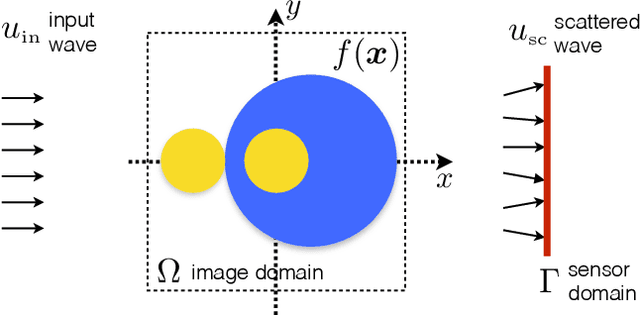
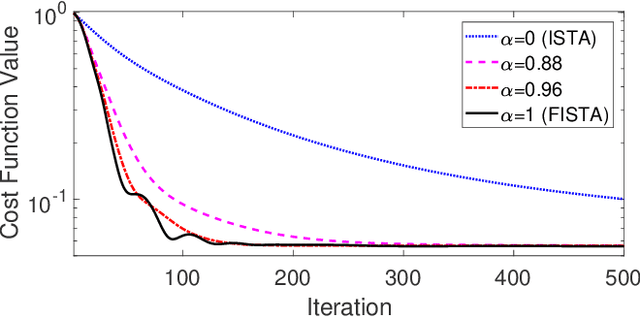
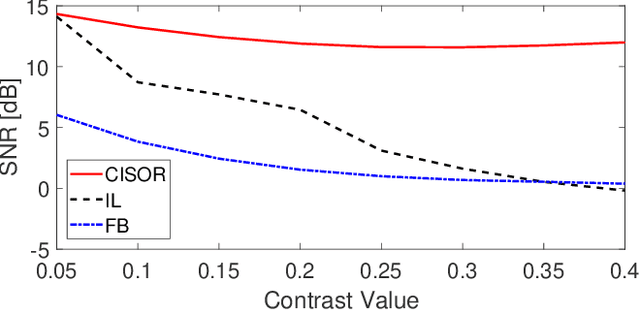
The problem of reconstructing an object from the measurements of the light it scatters is common in numerous imaging applications. While the most popular formulations of the problem are based on linearizing the object-light relationship, there is an increased interest in considering nonlinear formulations that can account for multiple light scattering. In this paper, we propose an image reconstruction method, called CISOR, for nonlinear diffractive imaging, based on a nonconvex optimization formulation with total variation (TV) regularization. The nonconvex solver used in CISOR is our new variant of fast iterative shrinkage/thresholding algorithm (FISTA). We provide fast and memory-efficient implementation of the new FISTA variant and prove that it reliably converges for our nonconvex optimization problem. In addition, we systematically compare our method with other state-of-the-art methods on simulated as well as experimentally measured data in both 2D and 3D settings.