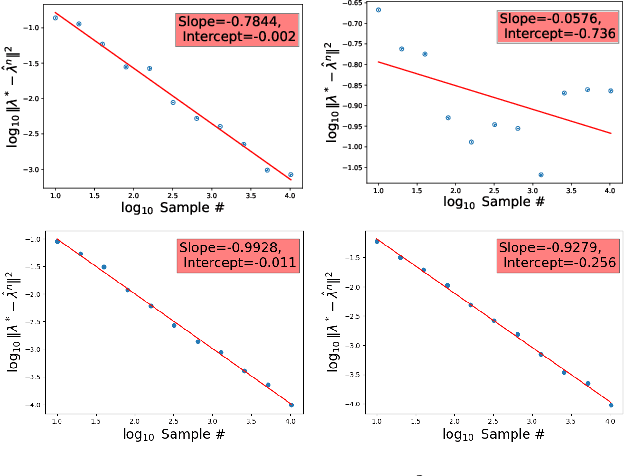
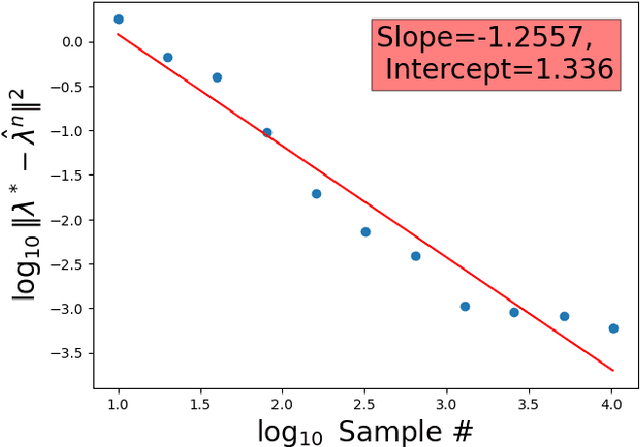
Synthesis and Analysis of Data as Probability Measures with Entropy-Regularized Optimal Transport

We consider synthesis and analysis of probability measures using the entropy-regularized Wasserstein-2 cost and its unbiased version, the Sinkhorn divergence. The synthesis problem consists of computing the barycenter, with respect to these costs, of $m$ reference measures given a set of coefficients belonging to the $m$-dimensional simplex. The analysis problem consists of finding the coefficients for the closest barycenter in the Wasserstein-2 distance to a given measure $\mu$. Under the weakest assumptions on the measures thus far in the literature, we compute the derivative of the entropy-regularized Wasserstein-2 cost. We leverage this to establish a characterization of regularized barycenters as solutions to a fixed-point equation for the average of the entropic maps from the barycenter to the reference measures. This characterization yields a finite-dimensional, convex, quadratic program for solving the analysis problem when $\mu$ is a barycenter. It is shown that these coordinates, as well as the value of the barycenter functional, can be estimated from samples with dimension-independent rates of convergence, a hallmark of entropy-regularized optimal transport, and we verify these rates experimentally. We also establish that barycentric coordinates are stable with respect to perturbations in the Wasserstein-2 metric, suggesting a robustness of these coefficients to corruptions. We employ the barycentric coefficients as features for classification of corrupted point cloud data, and show that compared to neural network baselines, our approach is more efficient in small training data regimes.

Linearized Wasserstein Barycenters: Synthesis, Analysis, Representational Capacity, and Applications

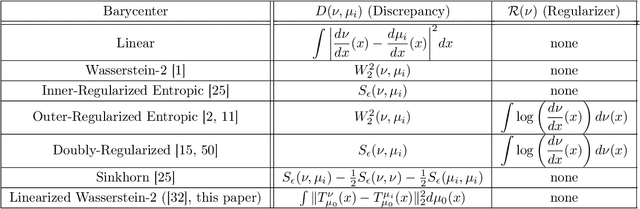
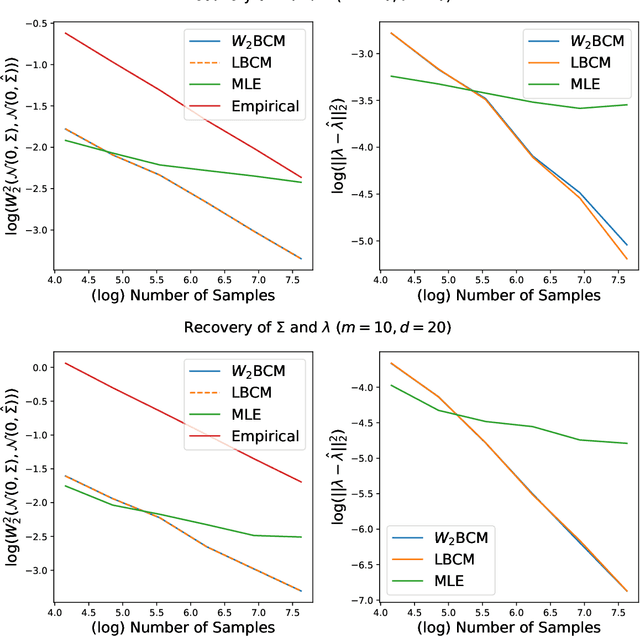
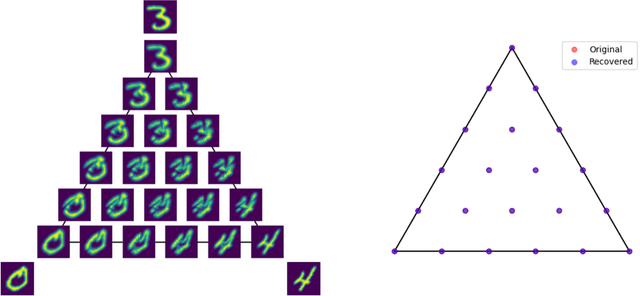
We propose the \textit{linear barycentric coding model (LBCM)} that utilizes the linear optimal transport (LOT) metric for analysis and synthesis of probability measures. We provide a closed-form solution to the variational problem characterizing the probability measures in the LBCM and establish equivalence of the LBCM to the set of Wasserstein-2 barycenters in the special case of compatible measures. Computational methods for synthesizing and analyzing measures in the LBCM are developed with finite sample guarantees. One of our main theoretical contributions is to identify an LBCM, expressed in terms of a simple family, which is sufficient to express all probability measures on the interval $[0,1]$. We show that a natural analogous construction of an LBCM in $\mathbb{R}^2$ fails, and we leave it as an open problem to identify the proper extension in more than one dimension. We conclude by demonstrating the utility of LBCM for covariance estimation and data imputation.

Estimation of entropy-regularized optimal transport maps between non-compactly supported measures

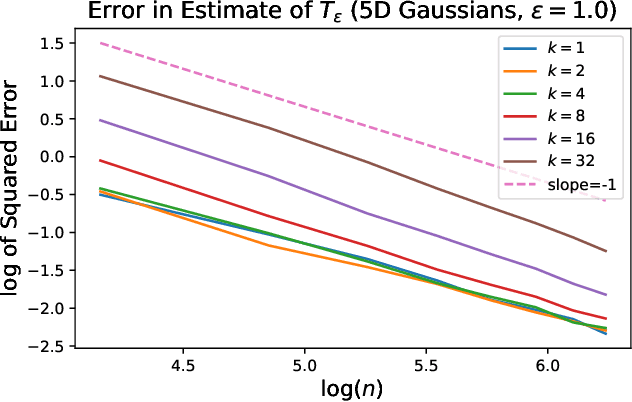
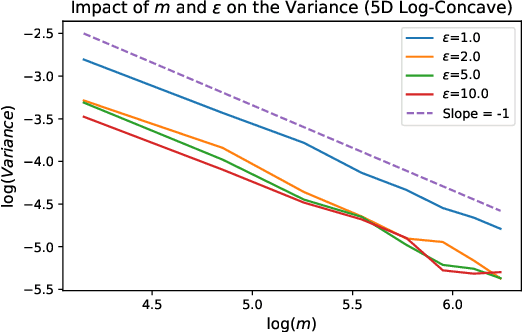
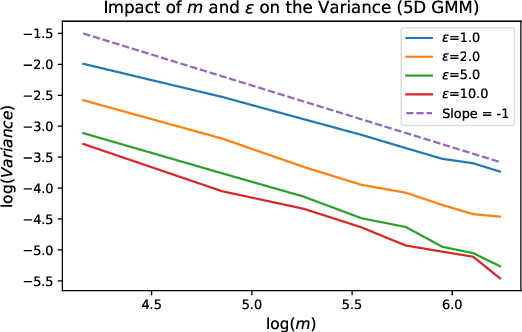
This paper addresses the problem of estimating entropy-regularized optimal transport (EOT) maps with squared-Euclidean cost between source and target measures that are subGaussian. In the case that the target measure is compactly supported or strongly log-concave, we show that for a recently proposed in-sample estimator, the expected squared $L^2$-error decays at least as fast as $O(n^{-1/3})$ where $n$ is the sample size. For the general subGaussian case we show that the expected $L^1$-error decays at least as fast as $O(n^{-1/6})$, and in both cases we have polynomial dependence on the regularization parameter. While these results are suboptimal compared to known results in the case of compactness of both the source and target measures (squared $L^2$-error converging at a rate $O(n^{-1})$) and for when the source is subGaussian while the target is compactly supported (squared $L^2$-error converging at a rate $O(n^{-1/2})$), their importance lie in eliminating the compact support requirements. The proof technique makes use of a bias-variance decomposition where the variance is controlled using standard concentration of measure results and the bias is handled by T1-transport inequalities along with sample complexity results in estimation of EOT cost under subGaussian assumptions. Our experimental results point to a looseness in controlling the variance terms and we conclude by posing several open problems.

On neural and dimensional collapse in supervised and unsupervised contrastive learning with hard negative sampling

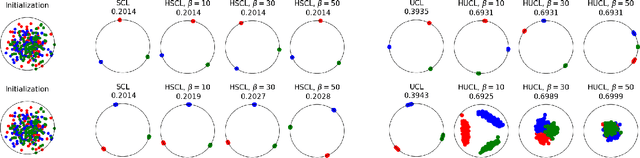
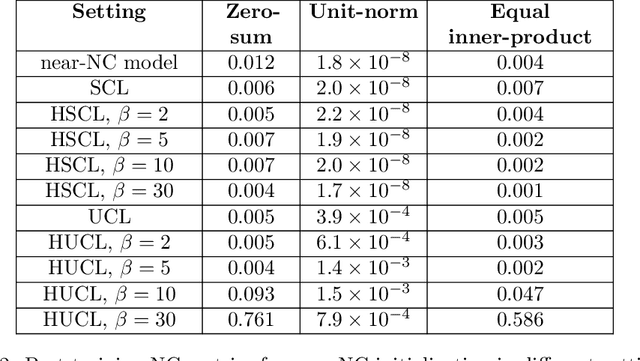
For a widely-studied data model and general loss and sample-hardening functions we prove that the Supervised Contrastive Learning (SCL), Hard-SCL (HSCL), and Unsupervised Contrastive Learning (UCL) risks are minimized by representations that exhibit Neural Collapse (NC), i.e., the class means form an Equianglular Tight Frame (ETF) and data from the same class are mapped to the same representation. We also prove that for any representation mapping, the HSCL and Hard-UCL (HUCL) risks are lower bounded by the corresponding SCL and UCL risks. Although the optimality of ETF is known for SCL, albeit only for InfoNCE loss, its optimality for HSCL and UCL under general loss and hardening functions is novel. Moreover, our proofs are much simpler, compact, and transparent. We empirically demonstrate, for the first time, that ADAM optimization of HSCL and HUCL risks with random initialization and suitable hardness levels can indeed converge to the NC geometry if we incorporate unit-ball or unit-sphere feature normalization. Without incorporating hard negatives or feature normalization, however, the representations learned via ADAM suffer from dimensional collapse (DC) and fail to attain the NC geometry.

Accuracy versus time frontiers of semi-supervised and self-supervised learning on medical images

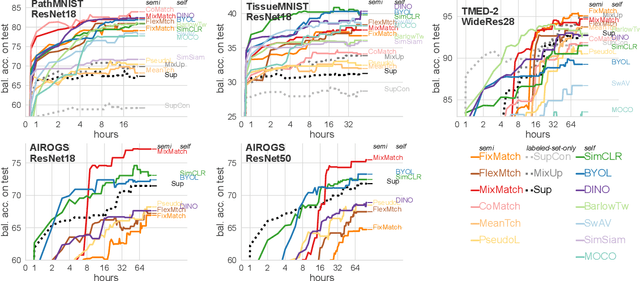
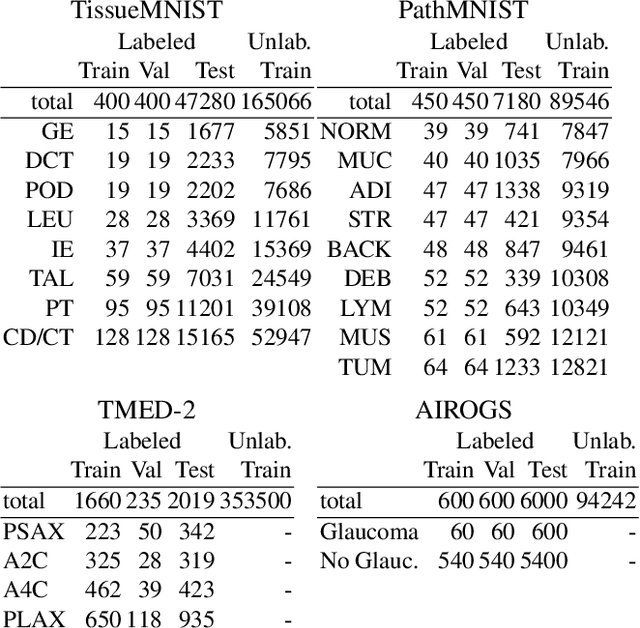
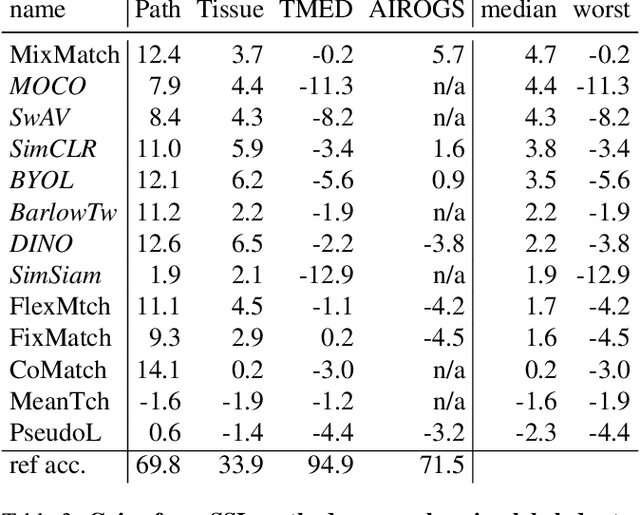
For many applications of classifiers to medical images, a trustworthy label for each image can be difficult or expensive to obtain. In contrast, images without labels are more readily available. Two major research directions both promise that additional unlabeled data can improve classifier performance: self-supervised learning pretrains useful representations on unlabeled data only, then fine-tunes a classifier on these representations via the labeled set; semi-supervised learning directly trains a classifier on labeled and unlabeled data simultaneously. Recent methods from both directions have claimed significant gains on non-medical tasks, but do not systematically assess medical images and mostly compare only to methods in the same direction. This study contributes a carefully-designed benchmark to help answer a practitioner's key question: given a small labeled dataset and a limited budget of hours to spend on training, what gains from additional unlabeled images are possible and which methods best achieve them? Unlike previous benchmarks, ours uses realistic-sized validation sets to select hyperparameters, assesses runtime-performance tradeoffs, and bridges two research fields. By comparing 6 semi-supervised methods and 5 self-supervised methods to strong labeled-only baselines on 3 medical datasets with 30-1000 labels per class, we offer insights to resource-constrained, results-focused practitioners: MixMatch, SimCLR, and BYOL represent strong choices that were not surpassed by more recent methods. After much effort selecting hyperparameters on one dataset, we publish settings that enable strong methods to perform well on new medical tasks within a few hours, with further search over dozens of hours delivering modest additional gains.

A principled approach to model validation in domain generalization

Domain generalization aims to learn a model with good generalization ability, that is, the learned model should not only perform well on several seen domains but also on unseen domains with different data distributions. State-of-the-art domain generalization methods typically train a representation function followed by a classifier jointly to minimize both the classification risk and the domain discrepancy. However, when it comes to model selection, most of these methods rely on traditional validation routines that select models solely based on the lowest classification risk on the validation set. In this paper, we theoretically demonstrate a trade-off between minimizing classification risk and mitigating domain discrepancy, i.e., it is impossible to achieve the minimum of these two objectives simultaneously. Motivated by this theoretical result, we propose a novel model selection method suggesting that the validation process should account for both the classification risk and the domain discrepancy. We validate the effectiveness of the proposed method by numerical results on several domain generalization datasets.

On Rank Energy Statistics via Optimal Transport: Continuity, Convergence, and Change Point Detection

This paper considers the use of recently proposed optimal transport-based multivariate test statistics, namely rank energy and its variant the soft rank energy derived from entropically regularized optimal transport, for the unsupervised nonparametric change point detection (CPD) problem. We show that the soft rank energy enjoys both fast rates of statistical convergence and robust continuity properties which lead to strong performance on real datasets. Our theoretical analyses remove the need for resampling and out-of-sample extensions previously required to obtain such rates. In contrast the rank energy suffers from the curse of dimensionality in statistical estimation and moreover can signal a change point from arbitrarily small perturbations, which leads to a high rate of false alarms in CPD. Additionally, under mild regularity conditions, we quantify the discrepancy between soft rank energy and rank energy in terms of the regularization parameter. Finally, we show our approach performs favorably in numerical experiments compared to several other optimal transport-based methods as well as maximum mean discrepancy.

Alternating minimization algorithm with initialization analysis for r-local and k-sparse unlabeled sensing

The unlabeled sensing problem is to recover an unknown signal from permuted linear measurements. We propose an alternating minimization algorithm with a suitable initialization for the widely considered k-sparse permutation model. Assuming either a Gaussian measurement matrix or a sub-Gaussian signal, we upper bound the initialization error for the r-local and k-sparse permutation models in terms of the block size $r$ and the number of shuffles k, respectively. Our algorithm is computationally scalable and, compared to baseline methods, achieves superior performance on real and synthetic datasets.

Trade-off between reconstruction loss and feature alignment for domain generalization

Domain generalization (DG) is a branch of transfer learning that aims to train the learning models on several seen domains and subsequently apply these pre-trained models to other unseen (unknown but related) domains. To deal with challenging settings in DG where both data and label of the unseen domain are not available at training time, the most common approach is to design the classifiers based on the domain-invariant representation features, i.e., the latent representations that are unchanged and transferable between domains. Contrary to popular belief, we show that designing classifiers based on invariant representation features alone is necessary but insufficient in DG. Our analysis indicates the necessity of imposing a constraint on the reconstruction loss induced by representation functions to preserve most of the relevant information about the label in the latent space. More importantly, we point out the trade-off between minimizing the reconstruction loss and achieving domain alignment in DG. Our theoretical results motivate a new DG framework that jointly optimizes the reconstruction loss and the domain discrepancy. Both theoretical and numerical results are provided to justify our approach.

Non-Parametric and Regularized Dynamical Wasserstein Barycenters for Time-Series Analysis

We consider probabilistic time-series models for systems that gradually transition among a finite number of states. We are particularly motivated by applications such as human activity analysis where the observed time-series contains segments representing distinct activities such as running or walking as well as segments characterized by continuous transition among these states. Accordingly, the dynamical Wasserstein barycenter (DWB) model introduced in Cheng et al. in 2021 [1] associates with each state, which we call a pure state, its own probability distribution, and models these continuous transitions with the dynamics of the barycentric weights that combine the pure state distributions via the Wasserstein barycenter. Here, focusing on the univariate case where Wasserstein distances and barycenters can be computed in closed form, we extend [1] by discussing two challenges associated with learning a DWB model and two improvements. First, we highlight the issue of uniqueness in identifying the model parameters. Secondly, we discuss the challenge of estimating a dynamically evolving distribution given a limited number of samples. The uncertainty associated with this estimation may cause a model's learned dynamics to not reflect the gradual transitions characteristic of the system. The first improvement introduces a regularization framework that addresses this uncertainty by imposing temporal smoothness on the dynamics of the barycentric weights while leveraging the understanding of the non-uniqueness of the problem. This is done without defining an entire stochastic model for the dynamics of the system as in [1]. Our second improvement lifts the Gaussian assumption on the pure states distributions in [1] by proposing a quantile-based non-parametric representation. We pose model estimation in a variational framework and propose a finite approximation to the infinite dimensional problem.