Non-Parametric and Regularized Dynamical Wasserstein Barycenters for Time-Series Analysis

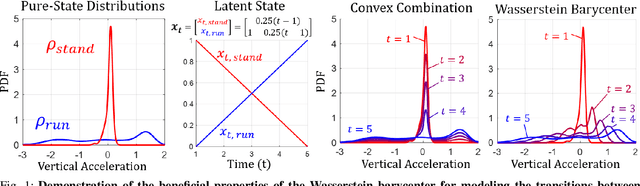
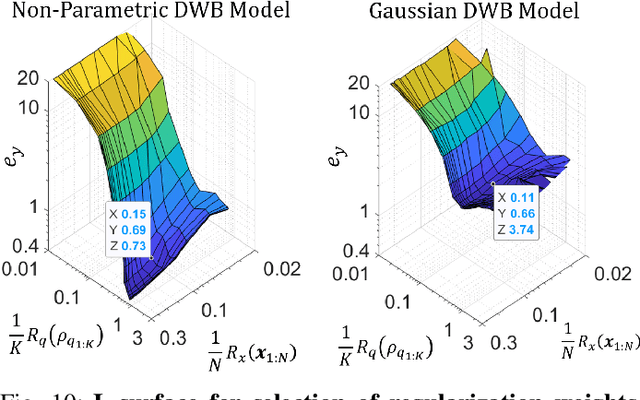
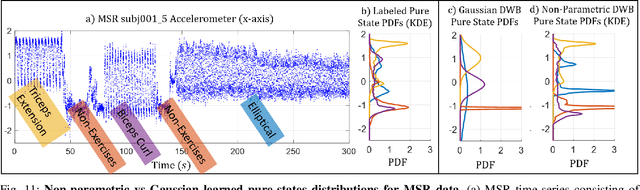
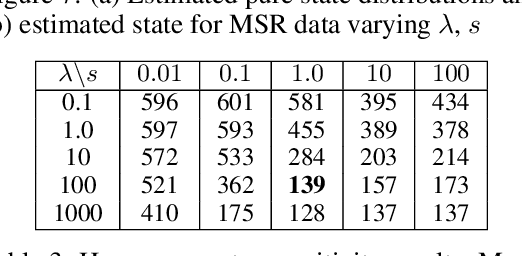
We consider probabilistic time-series models for systems that gradually transition among a finite number of states. We are particularly motivated by applications such as human activity analysis where the observed time-series contains segments representing distinct activities such as running or walking as well as segments characterized by continuous transition among these states. Accordingly, the dynamical Wasserstein barycenter (DWB) model introduced in Cheng et al. in 2021 [1] associates with each state, which we call a pure state, its own probability distribution, and models these continuous transitions with the dynamics of the barycentric weights that combine the pure state distributions via the Wasserstein barycenter. Here, focusing on the univariate case where Wasserstein distances and barycenters can be computed in closed form, we extend [1] by discussing two challenges associated with learning a DWB model and two improvements. First, we highlight the issue of uniqueness in identifying the model parameters. Secondly, we discuss the challenge of estimating a dynamically evolving distribution given a limited number of samples. The uncertainty associated with this estimation may cause a model's learned dynamics to not reflect the gradual transitions characteristic of the system. The first improvement introduces a regularization framework that addresses this uncertainty by imposing temporal smoothness on the dynamics of the barycentric weights while leveraging the understanding of the non-uniqueness of the problem. This is done without defining an entire stochastic model for the dynamics of the system as in [1]. Our second improvement lifts the Gaussian assumption on the pure states distributions in [1] by proposing a quantile-based non-parametric representation. We pose model estimation in a variational framework and propose a finite approximation to the infinite dimensional problem.

Easy Variational Inference for Categorical Models via an Independent Binary Approximation

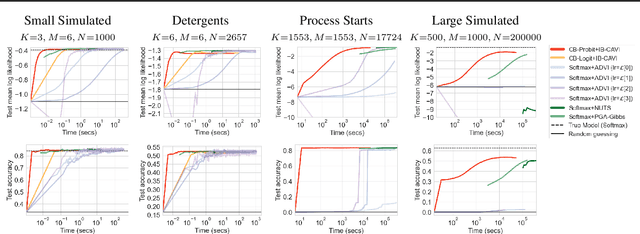
We pursue tractable Bayesian analysis of generalized linear models (GLMs) for categorical data. Thus far, GLMs are difficult to scale to more than a few dozen categories due to non-conjugacy or strong posterior dependencies when using conjugate auxiliary variable methods. We define a new class of GLMs for categorical data called categorical-from-binary (CB) models. Each CB model has a likelihood that is bounded by the product of binary likelihoods, suggesting a natural posterior approximation. This approximation makes inference straightforward and fast; using well-known auxiliary variables for probit or logistic regression, the product of binary models admits conjugate closed-form variational inference that is embarrassingly parallel across categories and invariant to category ordering. Moreover, an independent binary model simultaneously approximates multiple CB models. Bayesian model averaging over these can improve the quality of the approximation for any given dataset. We show that our approach scales to thousands of categories, outperforming posterior estimation competitors like Automatic Differentiation Variational Inference (ADVI) and No U-Turn Sampling (NUTS) in the time required to achieve fixed prediction quality.

Dynamical Wasserstein Barycenters for Time-series Modeling

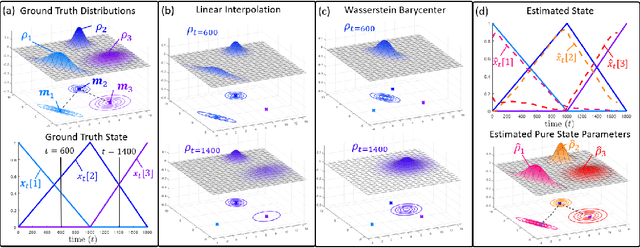
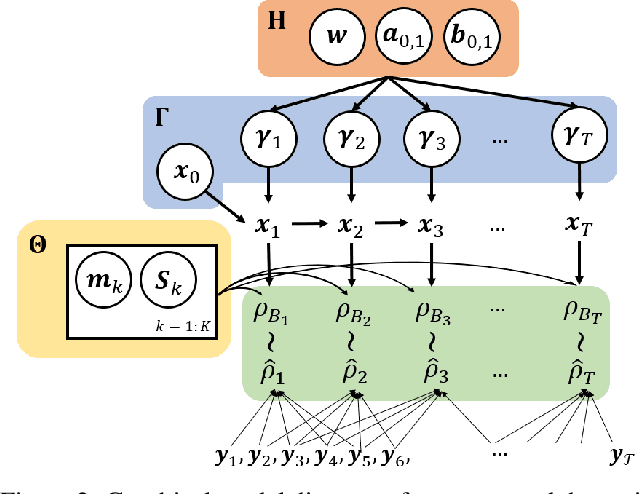
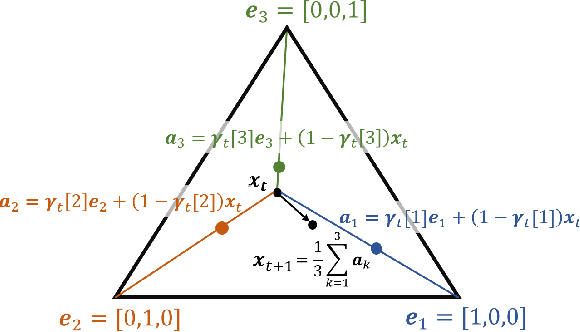
Many time series can be modeled as a sequence of segments representing high-level discrete states, such as running and walking in a human activity application. Flexible models should describe the system state and observations in stationary "pure-state" periods as well as transition periods between adjacent segments, such as a gradual slowdown between running and walking. However, most prior work assumes instantaneous transitions between pure discrete states. We propose a dynamical Wasserstein barycentric (DWB) model that estimates the system state over time as well as the data-generating distributions of pure states in an unsupervised manner. Our model assumes each pure state generates data from a multivariate normal distribution, and characterizes transitions between states via displacement-interpolation specified by the Wasserstein barycenter. The system state is represented by a barycentric weight vector which evolves over time via a random walk on the simplex. Parameter learning leverages the natural Riemannian geometry of Gaussian distributions under the Wasserstein distance, which leads to improved convergence speeds. Experiments on several human activity datasets show that our proposed DWB model accurately learns the generating distribution of pure states while improving state estimation for transition periods compared to the commonly used linear interpolation mixture models.

On Matched Filtering for Statistical Change Point Detection

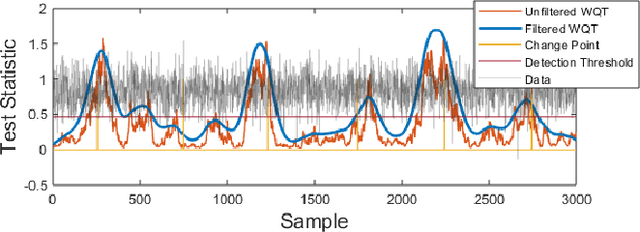
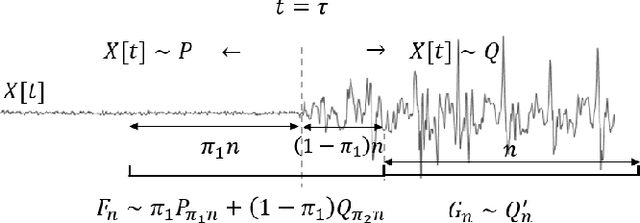
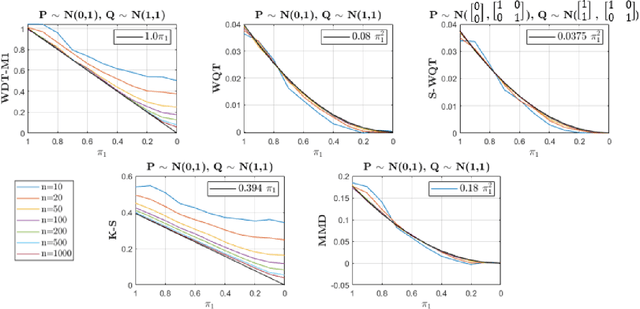
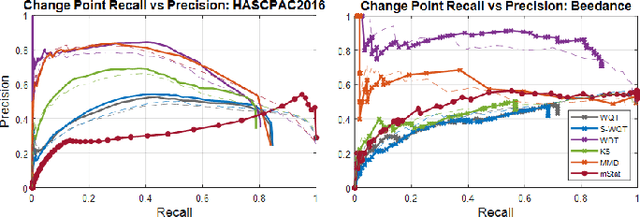
Non-parametric and distribution-free two-sample tests have been the foundation of many change point detection algorithms.However, noise in the data make these tests susceptible to false positives and localization ambiguity. We address these issues by deriving asymptotically matched filters under standard IID assumptions on the data for various sliding window two-sample tests.In particular, in this paper we focus on the Wasserstein quantile test, the Wasserstein-1 distance test, maximum mean discrepancy(MMD) test, and the Kolmogorov-Smirnov (KS) test. To the best of our knowledge this is the first time an matched filtering has been proposed and evaluated for these tests or for change point detection. While in this paper we only consider a subset of tests, the proposed methodology and analysis can be extended to other tests. Quite remarkably, this simple post processing turns out to be quite robust in terms of mitigating false positives and improving change point localization, thereby making these distribution-free tests practically useful. We demonstrate this through experiments on synthetic data as well as activity recognition benchmarks. We further highlight and contrast several properties such as sensitivity of these tests and compare their relative performance.

Optimal Transport Based Change Point Detection and Time Series Segment Clustering

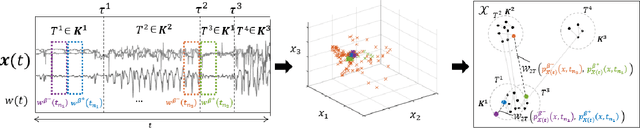
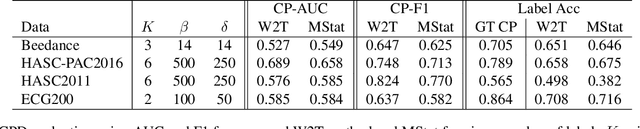
Two common problems in time series analysis are the decomposition of the data stream into disjoint segments, each of which is in some sense 'homogeneous' - a problem that is also referred to as Change Point Detection (CPD) - and the grouping of similar nonadjacent segments, or Time Series Segment Clustering (TSSC). Building upon recent theoretical advances characterizing the limiting distribution free behavior of the Wasserstein two-sample test, we propose a novel algorithm for unsupervised, distribution-free CPD, which is amenable to both offline and online settings. We also introduce a method to mitigate false positives in CPD, and address TSSC by using the Wasserstein distance between the detected segments to build an affinity matrix to which we apply spectral clustering. Results on both synthetic and real data sets show the benefits of the approach.

Ensemble Multi-task Gaussian Process Regression with Multiple Latent Processes

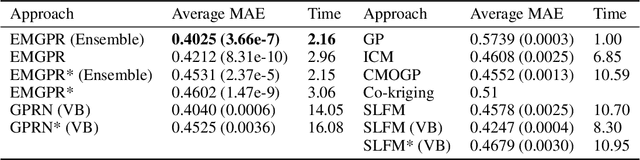
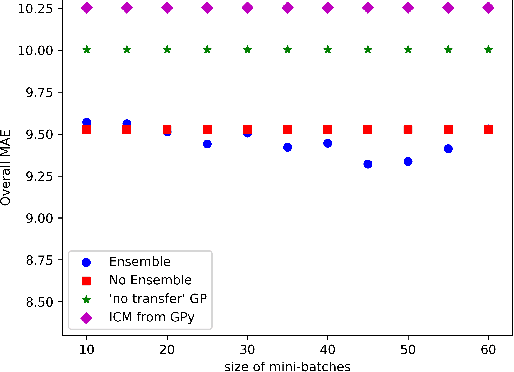
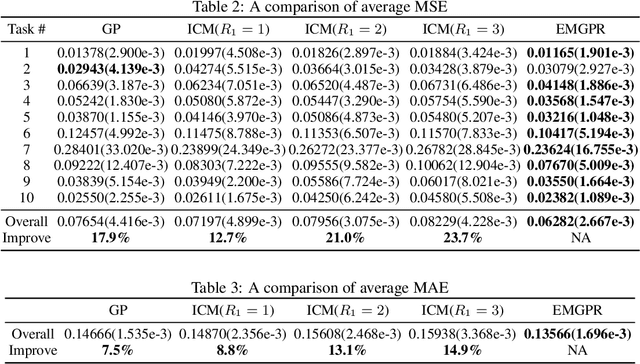
Multi-task/Multi-output learning seeks to exploit correlation among tasks to enhance performance over learning or solving each task independently. In this paper, we investigate this problem in the context of Gaussian Processes (GPs) and propose a new model which learns a mixture of latent processes by decomposing the covariance matrix into a sum of structured hidden components each of which is controlled by a latent GP over input features and a "weight" over tasks. From this sum structure, we propose a parallelizable parameter learning algorithm with a predetermined initialization for the "weights". We also notice that an ensemble parameter learning approach using mini-batches of training data not only reduces the computation complexity of learning but also improves the regression performance. We evaluate our model on two datasets, the smaller Swiss Jura dataset and another relatively larger ATMS dataset from NOAA. Substantial improvements are observed compared with established alternatives.

On the Fusion of Compton Scatter and Attenuation Data for Limited-view X-ray Tomographic Applications

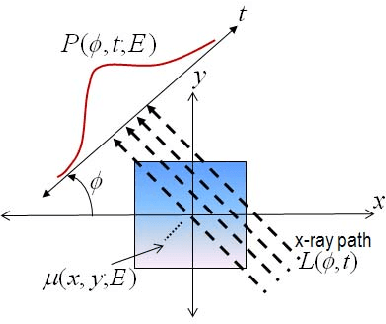
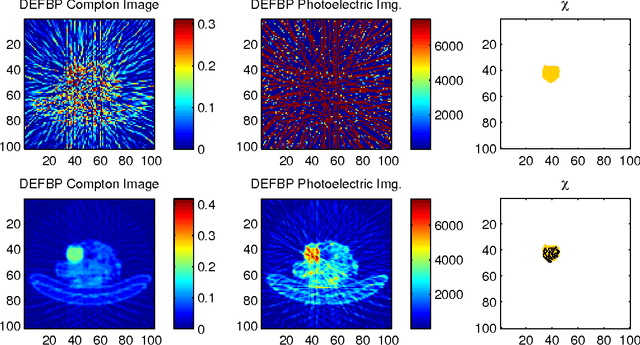
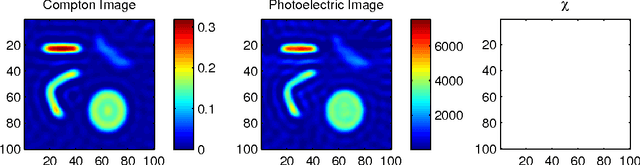
In this paper we demonstrate the utility of fusing energy-resolved observations of Compton scattered photons with traditional attenuation data for the joint recovery of mass density and photoelectric absorption in the context of limited view tomographic imaging applications. We begin with the development of a physical and associated numerical model for the Compton scatter process. Using this model, we propose a variational approach recovering these two material properties. In addition to the typical data-fidelity terms, the optimization functional includes regularization for both the mass density and photoelectric coefficients. We consider a novel edge-preserving method in the case of mass density. To aid in the recovery of the photoelectric information, we draw on our recent method in \cite{r15} and employ a non-local regularization scheme that builds on the fact that mass density is more stably imaged. Simulation results demonstrate clear advantages associated with the use of both scattered photon data and energy resolved information in mapping the two material properties of interest. Specifically, comparing images obtained using only conventional attenuation data with those where we employ only Compton scatter photons and images formed from the combination of the two, shows that taking advantage of both types of data for reconstruction provides far more accurate results.

Stabilizing dual-energy X-ray computed tomography reconstructions using patch-based regularization

Recent years have seen growing interest in exploiting dual- and multi-energy measurements in computed tomography (CT) in order to characterize material properties as well as object shape. Material characterization is performed by decomposing the scene into constitutive basis functions, such as Compton scatter and photoelectric absorption functions. While well motivated physically, the joint recovery of the spatial distribution of photoelectric and Compton properties is severely complicated by the fact that the data are several orders of magnitude more sensitive to Compton scatter coefficients than to photoelectric absorption, so small errors in Compton estimates can create large artifacts in the photoelectric estimate. To address these issues, we propose a model-based iterative approach which uses patch-based regularization terms to stabilize inversion of photoelectric coefficients, and solve the resulting problem though use of computationally attractive Alternating Direction Method of Multipliers (ADMM) solution techniques. Using simulations and experimental data acquired on a commercial scanner, we demonstrate that the proposed processing can lead to more stable material property estimates which should aid materials characterization in future dual- and multi-energy CT systems.

Tensor-based formulation and nuclear norm regularization for multi-energy computed tomography

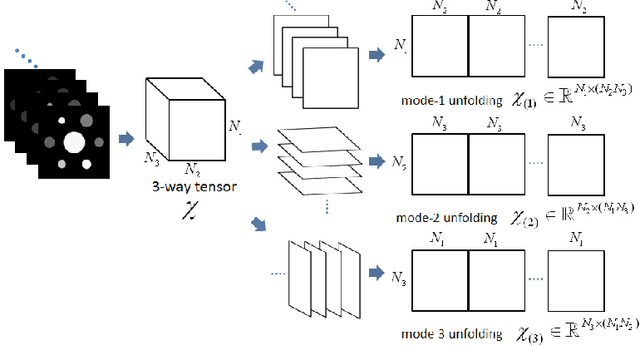
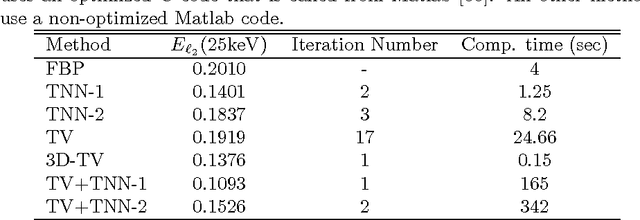
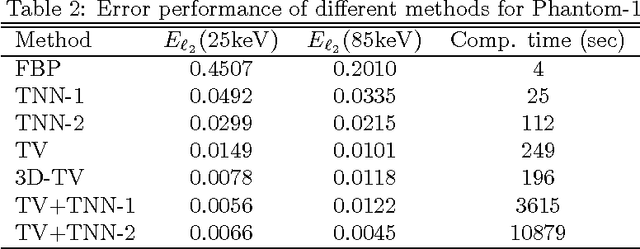
The development of energy selective, photon counting X-ray detectors allows for a wide range of new possibilities in the area of computed tomographic image formation. Under the assumption of perfect energy resolution, here we propose a tensor-based iterative algorithm that simultaneously reconstructs the X-ray attenuation distribution for each energy. We use a multi-linear image model rather than a more standard "stacked vector" representation in order to develop novel tensor-based regularizers. Specifically, we model the multi-spectral unknown as a 3-way tensor where the first two dimensions are space and the third dimension is energy. This approach allows for the design of tensor nuclear norm regularizers, which like its two dimensional counterpart, is a convex function of the multi-spectral unknown. The solution to the resulting convex optimization problem is obtained using an alternating direction method of multipliers (ADMM) approach. Simulation results shows that the generalized tensor nuclear norm can be used as a stand alone regularization technique for the energy selective (spectral) computed tomography (CT) problem and when combined with total variation regularization it enhances the regularization capabilities especially at low energy images where the effects of noise are most prominent.

A Parametric Level Set Approach to Simultaneous Object Identification and Background Reconstruction for Dual Energy Computed Tomography

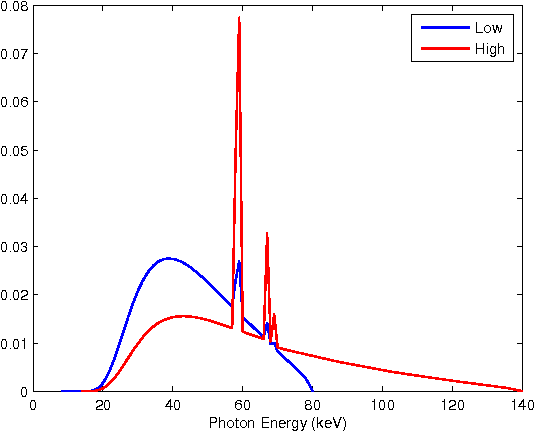
Dual energy computerized tomography has gained great interest because of its ability to characterize the chemical composition of a material rather than simply providing relative attenuation images as in conventional tomography. The purpose of this paper is to introduce a novel polychromatic dual energy processing algorithm with an emphasis on detection and characterization of piecewise constant objects embedded in an unknown, cluttered background. Physical properties of the objects, specifically the Compton scattering and photoelectric absorption coefficients, are assumed to be known with some level of uncertainty. Our approach is based on a level-set representation of the characteristic function of the object and encompasses a number of regularization techniques for addressing both the prior information we have concerning the physical properties of the object as well as fundamental, physics-based limitations associated with our ability to jointly recover the Compton scattering and photoelectric absorption properties of the scene. In the absence of an object with appropriate physical properties, our approach returns a null characteristic function and thus can be viewed as simultaneously solving the detection and characterization problems. Unlike the vast majority of methods which define the level set function non-parametrically, i.e., as a dense set of pixel values), we define our level set parametrically via radial basis functions (RBF's) and employ a Gauss-Newton type algorithm for cost minimization. Numerical results show that the algorithm successfully detects objects of interest, finds their shape and location, and gives a adequate reconstruction of the background.