Using machine learning to measure evidence of students' sensemaking in physics courses

In the education system, problem-solving correctness is often inappropriately conflated with student learning. Advances in both Physics Education Research (PER) and Machine Learning (ML) provide the initial tools to develop a more meaningful and efficient measurement scheme for whether physics students are engaging in sensemaking: a learning process of figuring out the how and why for a particular phenomena. In this work, we contribute such a measurement scheme, which quantifies the evidence of students' physical sensemaking given their written explanations for their solutions to physics problems. We outline how the proposed human annotation scheme can be automated into a deployable ML model using language encoders and shared probabilistic classifiers. The procedure is scalable for a large number of problems and students. We implement three unique language encoders with logistic regression, and provide a deployability analysis on 385 real student explanations from the 2023 Introduction to Physics course at Tufts University. Furthermore, we compute sensemaking scores for all students, and analyze these measurements alongside their corresponding problem-solving accuracies. We find no linear relationship between these two variables, supporting the hypothesis that one is not a reliable proxy for the other. We discuss how sensemaking scores can be used alongside problem-solving accuracies to provide a more nuanced snapshot of student performance in physics class.

Decision-aware training of spatiotemporal forecasting models

Optimal allocation of scarce resources is a common problem for decision makers faced with choosing a limited number of locations for intervention. Spatiotemporal prediction models could make such decisions data-driven. A recent performance metric called fraction of best possible reach (BPR) measures the impact of using a model's recommended size K subset of sites compared to the best possible top-K in hindsight. We tackle two open problems related to BPR. First, we explore how to rank all sites numerically given a probabilistic model that predicts event counts jointly across sites. Ranking via the per-site mean is suboptimal for BPR. Instead, we offer a better ranking for BPR backed by decision theory. Second, we explore how to train a probabilistic model's parameters to maximize BPR. Discrete selection of K sites implies all-zero parameter gradients which prevent standard gradient training. We overcome this barrier via advances in perturbed optimizers. We further suggest a training objective that combines likelihood with a decision-aware BPR constraint to deliver high-quality top-K rankings as well as good forecasts for all sites. We demonstrate our approach on two where-to-intervene applications: mitigating opioid-related fatal overdoses for public health and monitoring endangered wildlife.

Learning Hyperparameters via a Data-Emphasized Variational Objective

When training large flexible models, practitioners often rely on grid search to select hyperparameters that control over-fitting. This grid search has several disadvantages: the search is computationally expensive, requires carving out a validation set that reduces the available data for training, and requires users to specify candidate values. In this paper, we propose an alternative: directly learning regularization hyperparameters on the full training set via the evidence lower bound ("ELBo") objective from variational methods. For deep neural networks with millions of parameters, we recommend a modified ELBo that upweights the influence of the data likelihood relative to the prior. Our proposed technique overcomes all three disadvantages of grid search. In a case study on transfer learning of image classifiers, we show how our method reduces the 88+ hour grid search of past work to under 3 hours while delivering comparable accuracy. We further demonstrate how our approach enables efficient yet accurate approximations of Gaussian processes with learnable length-scale kernels.

Learning the Regularization Strength for Deep Fine-Tuning via a Data-Emphasized Variational Objective

A number of popular transfer learning methods rely on grid search to select regularization hyperparameters that control over-fitting. This grid search requirement has several key disadvantages: the search is computationally expensive, requires carving out a validation set that reduces the size of available data for model training, and requires practitioners to specify candidate values. In this paper, we propose an alternative to grid search: directly learning regularization hyperparameters on the full training set via model selection techniques based on the evidence lower bound ("ELBo") objective from variational methods. For deep neural networks with millions of parameters, we specifically recommend a modified ELBo that upweights the influence of the data likelihood relative to the prior while remaining a valid bound on the evidence for Bayesian model selection. Our proposed technique overcomes all three disadvantages of grid search. We demonstrate effectiveness on image classification tasks on several datasets, yielding heldout accuracy comparable to existing approaches with far less compute time.

Transfer Learning with Informative Priors: Simple Baselines Better than Previously Reported

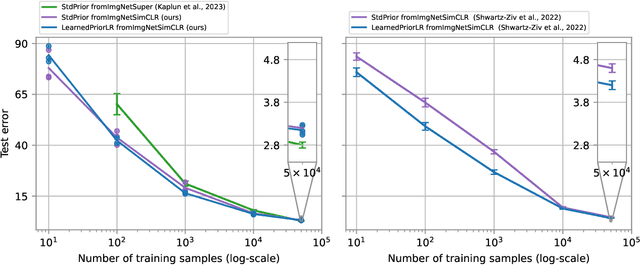
We pursue transfer learning to improve classifier accuracy on a target task with few labeled examples available for training. Recent work suggests that using a source task to learn a prior distribution over neural net weights, not just an initialization, can boost target task performance. In this study, we carefully compare transfer learning with and without source task informed priors across 5 datasets. We find that standard transfer learning informed by an initialization only performs far better than reported in previous comparisons. The relative gains of methods using informative priors over standard transfer learning vary in magnitude across datasets. For the scenario of 5-300 examples per class, we find negative or negligible gains on 2 datasets, modest gains (between 1.5-3 points of accuracy) on 2 other datasets, and substantial gains (>8 points) on one dataset. Among methods using informative priors, we find that an isotropic covariance appears competitive with learned low-rank covariance matrix while being substantially simpler to understand and tune. Further analysis suggests that the mechanistic justification for informed priors -- hypothesized improved alignment between train and test loss landscapes -- is not consistently supported due to high variability in empirical landscapes. We release code to allow independent reproduction of all experiments.

InterLUDE: Interactions between Labeled and Unlabeled Data to Enhance Semi-Supervised Learning

Semi-supervised learning (SSL) seeks to enhance task performance by training on both labeled and unlabeled data. Mainstream SSL image classification methods mostly optimize a loss that additively combines a supervised classification objective with a regularization term derived solely from unlabeled data. This formulation neglects the potential for interaction between labeled and unlabeled images. In this paper, we introduce InterLUDE, a new approach to enhance SSL made of two parts that each benefit from labeled-unlabeled interaction. The first part, embedding fusion, interpolates between labeled and unlabeled embeddings to improve representation learning. The second part is a new loss, grounded in the principle of consistency regularization, that aims to minimize discrepancies in the model's predictions between labeled versus unlabeled inputs. Experiments on standard closed-set SSL benchmarks and a medical SSL task with an uncurated unlabeled set show clear benefits to our approach. On the STL-10 dataset with only 40 labels, InterLUDE achieves 3.2% error rate, while the best previous method reports 14.9%.

Semi-Supervised Multimodal Multi-Instance Learning for Aortic Stenosis Diagnosis

Automated interpretation of ultrasound imaging of the heart (echocardiograms) could improve the detection and treatment of aortic stenosis (AS), a deadly heart disease. However, existing deep learning pipelines for assessing AS from echocardiograms have two key limitations. First, most methods rely on limited 2D cineloops, thereby ignoring widely available Doppler imaging that contains important complementary information about pressure gradients and blood flow abnormalities associated with AS. Second, obtaining labeled data is difficult. There are often far more unlabeled echocardiogram recordings available, but these remain underutilized by existing methods. To overcome these limitations, we introduce Semi-supervised Multimodal Multiple-Instance Learning (SMMIL), a new deep learning framework for automatic interpretation for structural heart diseases like AS. When deployed, SMMIL can combine information from two input modalities, spectral Dopplers and 2D cineloops, to produce a study-level AS diagnosis. During training, SMMIL can combine a smaller labeled set and an abundant unlabeled set of both modalities to improve its classifier. Experiments demonstrate that SMMIL outperforms recent alternatives at 3-level AS severity classification as well as several clinically relevant AS detection tasks.

Discovering group dynamics in synchronous time series via hierarchical recurrent switching-state models

We seek to model a collection of time series arising from multiple entities interacting over the same time period. Recent work focused on modeling individual time series is inadequate for our intended applications, where collective system-level behavior influences the trajectories of individual entities. To address such problems, we present a new hierarchical switching-state model that can be trained in an unsupervised fashion to simultaneously explain both system-level and individual-level dynamics. We employ a latent system-level discrete state Markov chain that drives latent entity-level chains which in turn govern the dynamics of each observed time series. Feedback from the observations to the chains at both the entity and system levels improves flexibility via context-dependent state transitions. Our hierarchical switching recurrent dynamical models can be learned via closed-form variational coordinate ascent updates to all latent chains that scale linearly in the number of individual time series. This is asymptotically no more costly than fitting separate models for each entity. Experiments on synthetic and real datasets show that our model can produce better forecasts of future entity behavior than existing methods. Moreover, the availability of latent state chains at both the entity and system level enables interpretation of group dynamics.

A Probabilistic Method to Predict Classifier Accuracy on Larger Datasets given Small Pilot Data

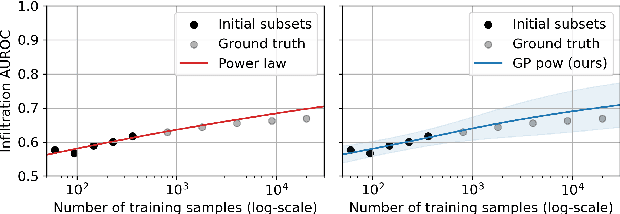
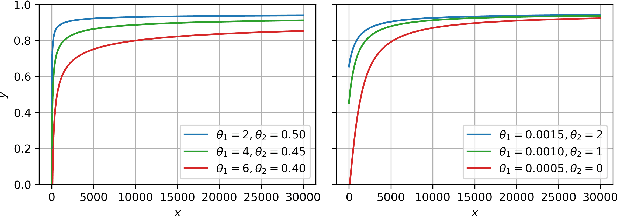
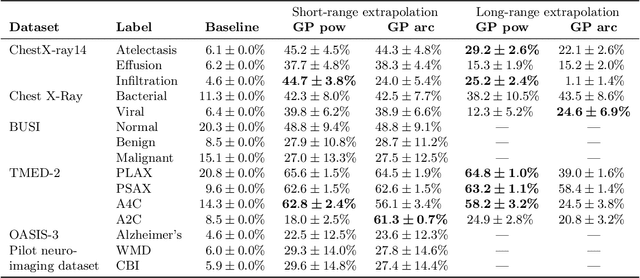
Practitioners building classifiers often start with a smaller pilot dataset and plan to grow to larger data in the near future. Such projects need a toolkit for extrapolating how much classifier accuracy may improve from a 2x, 10x, or 50x increase in data size. While existing work has focused on finding a single "best-fit" curve using various functional forms like power laws, we argue that modeling and assessing the uncertainty of predictions is critical yet has seen less attention. In this paper, we propose a Gaussian process model to obtain probabilistic extrapolations of accuracy or similar performance metrics as dataset size increases. We evaluate our approach in terms of error, likelihood, and coverage across six datasets. Though we focus on medical tasks and image modalities, our open source approach generalizes to any kind of classifier.

SINCERE: Supervised Information Noise-Contrastive Estimation REvisited

The information noise-contrastive estimation (InfoNCE) loss function provides the basis of many self-supervised deep learning methods due to its strong empirical results and theoretic motivation. Previous work suggests a supervised contrastive (SupCon) loss to extend InfoNCE to learn from available class labels. This SupCon loss has been widely-used due to reports of good empirical performance. However, in this work we suggest that the specific SupCon loss formulated by prior work has questionable theoretic justification, because it can encourage images from the same class to repel one another in the learned embedding space. This problematic behavior gets worse as the number of inputs sharing one class label increases. We propose the Supervised InfoNCE REvisited (SINCERE) loss as a remedy. SINCERE is a theoretically justified solution for a supervised extension of InfoNCE that never causes images from the same class to repel one another. We further show that minimizing our new loss is equivalent to maximizing a bound on the KL divergence between class conditional embedding distributions. We compare SINCERE and SupCon losses in terms of learning trajectories during pretraining and in ultimate linear classifier performance after finetuning. Our proposed SINCERE loss better separates embeddings from different classes during pretraining while delivering competitive accuracy.