Discovering group dynamics in synchronous time series via hierarchical recurrent switching-state models

We seek to model a collection of time series arising from multiple entities interacting over the same time period. Recent work focused on modeling individual time series is inadequate for our intended applications, where collective system-level behavior influences the trajectories of individual entities. To address such problems, we present a new hierarchical switching-state model that can be trained in an unsupervised fashion to simultaneously explain both system-level and individual-level dynamics. We employ a latent system-level discrete state Markov chain that drives latent entity-level chains which in turn govern the dynamics of each observed time series. Feedback from the observations to the chains at both the entity and system levels improves flexibility via context-dependent state transitions. Our hierarchical switching recurrent dynamical models can be learned via closed-form variational coordinate ascent updates to all latent chains that scale linearly in the number of individual time series. This is asymptotically no more costly than fitting separate models for each entity. Experiments on synthetic and real datasets show that our model can produce better forecasts of future entity behavior than existing methods. Moreover, the availability of latent state chains at both the entity and system level enables interpretation of group dynamics.

Flexible Models for Microclustering with Application to Entity Resolution

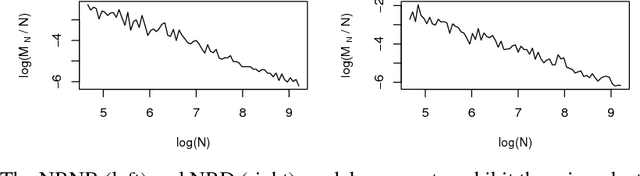
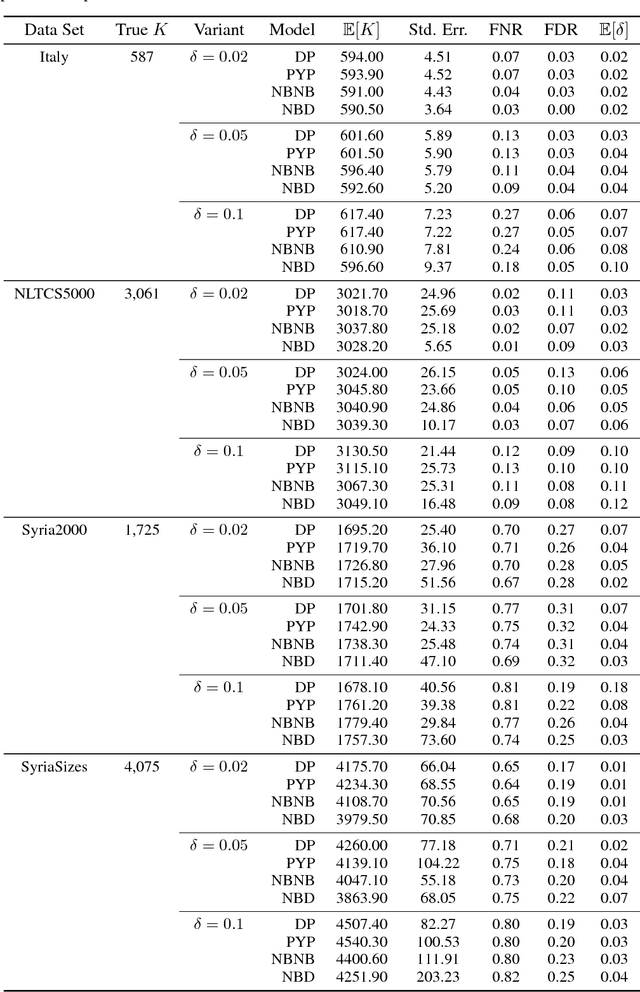
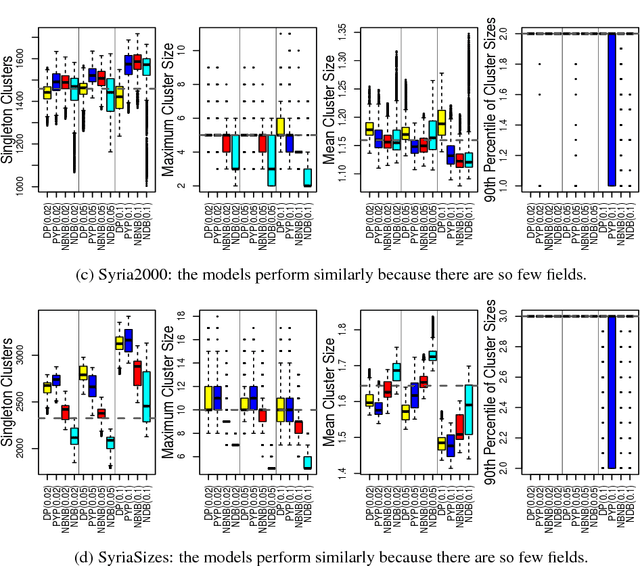
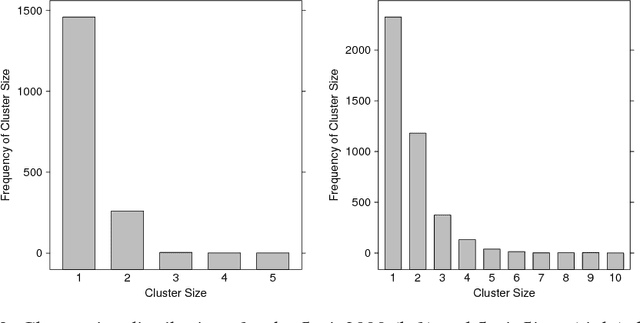
Most generative models for clustering implicitly assume that the number of data points in each cluster grows linearly with the total number of data points. Finite mixture models, Dirichlet process mixture models, and Pitman--Yor process mixture models make this assumption, as do all other infinitely exchangeable clustering models. However, for some applications, this assumption is inappropriate. For example, when performing entity resolution, the size of each cluster should be unrelated to the size of the data set, and each cluster should contain a negligible fraction of the total number of data points. These applications require models that yield clusters whose sizes grow sublinearly with the size of the data set. We address this requirement by defining the microclustering property and introducing a new class of models that can exhibit this property. We compare models within this class to two commonly used clustering models using four entity-resolution data sets.

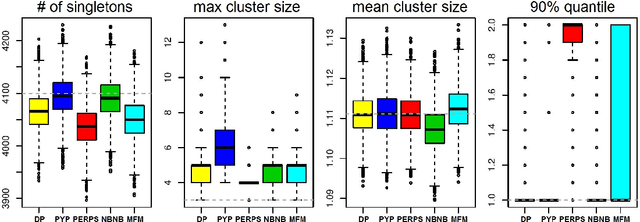
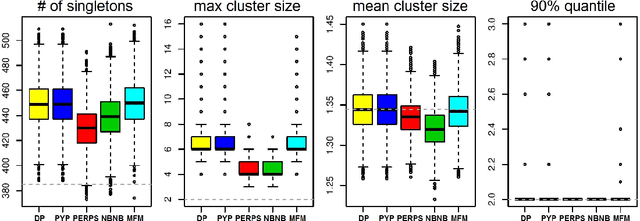
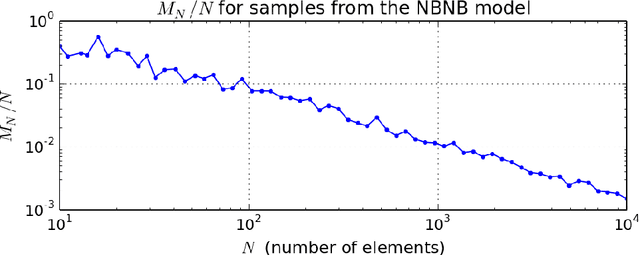
Microclustering: When the Cluster Sizes Grow Sublinearly with the Size of the Data Set

Most generative models for clustering implicitly assume that the number of data points in each cluster grows linearly with the total number of data points. Finite mixture models, Dirichlet process mixture models, and Pitman--Yor process mixture models make this assumption, as do all other infinitely exchangeable clustering models. However, for some tasks, this assumption is undesirable. For example, when performing entity resolution, the size of each cluster is often unrelated to the size of the data set. Consequently, each cluster contains a negligible fraction of the total number of data points. Such tasks therefore require models that yield clusters whose sizes grow sublinearly with the size of the data set. We address this requirement by defining the \emph{microclustering property} and introducing a new model that exhibits this property. We compare this model to several commonly used clustering models by checking model fit using real and simulated data sets.