A Primer on the Data Cleaning Pipeline

The availability of both structured and unstructured databases, such as electronic health data, social media data, patent data, and surveys that are often updated in real time, among others, has grown rapidly over the past decade. With this expansion, the statistical and methodological questions around data integration, or rather merging multiple data sources, has also grown. Specifically, the science of the ``data cleaning pipeline'' contains four stages that allow an analyst to perform downstream tasks, predictive analyses, or statistical analyses on ``cleaned data.'' This article provides a review of this emerging field, introducing technical terminology and commonly used methods.

(Almost) All of Entity Resolution

Whether the goal is to estimate the number of people that live in a congressional district, to estimate the number of individuals that have died in an armed conflict, or to disambiguate individual authors using bibliographic data, all these applications have a common theme - integrating information from multiple sources. Before such questions can be answered, databases must be cleaned and integrated in a systematic and accurate way, commonly known as record linkage, de-duplication, or entity resolution. In this article, we review motivational applications and seminal papers that have led to the growth of this area. Specifically, we review the foundational work that began in the 1940's and 50's that have led to modern probabilistic record linkage. We review clustering approaches to entity resolution, semi- and fully supervised methods, and canonicalization, which are being used throughout industry and academia in applications such as human rights, official statistics, medicine, citation networks, among others. Finally, we discuss current research topics of practical importance.

d-blink: Distributed End-to-End Bayesian Entity Resolution

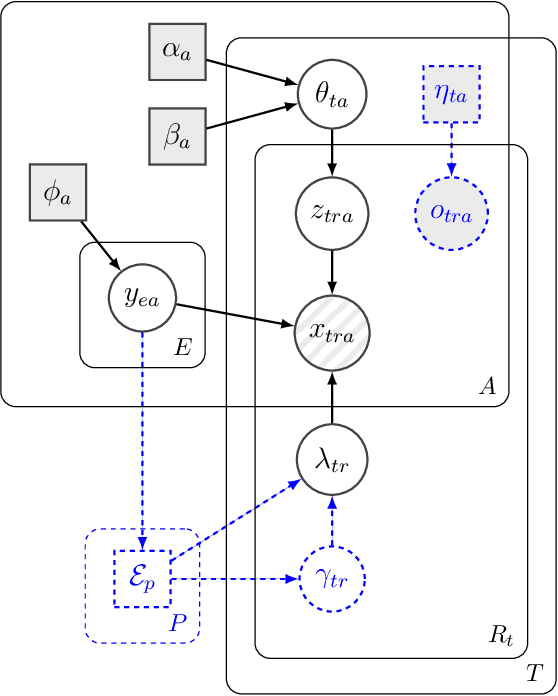
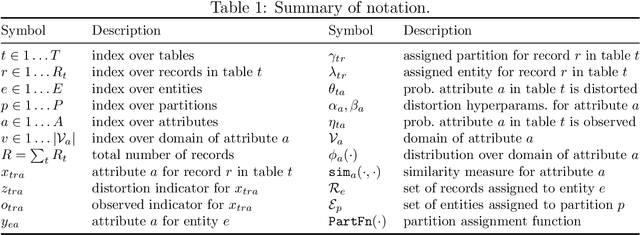
Entity resolution (ER) (record linkage or de-duplication) is the process of merging together noisy databases, often in the absence of a unique identifier. A major advancement in ER methodology has been the application of Bayesian generative models. Such models provide a natural framework for clustering records to unobserved (latent) entities, while providing exact uncertainty quantification and tight performance bounds. Despite these advancements, existing models do not scale to realistically-sized databases (larger than 1000 records) and they do not incorporate probabilistic blocking. In this paper, we propose "distributed Bayesian linkage" or d-blink -- the first scalable and distributed end-to-end Bayesian model for ER, which propagates uncertainty in blocking, matching and merging. We make several novel contributions, including: (i) incorporating probabilistic blocking directly into the model through auxiliary partitions; (ii) support for missing values; (iii) a partially-collapsed Gibbs sampler; and (iv) a novel perturbation sampling algorithm (leveraging the Vose-Alias method) that enables fast updates of the entity attributes. Finally, we conduct experiments on five data sets which show that d-blink can achieve significant efficiency gains -- in excess of 300$\times$ -- when compared to existing non-distributed methods.

Probabilistic Blocking with An Application to the Syrian Conflict

Entity resolution seeks to merge databases as to remove duplicate entries where unique identifiers are typically unknown. We review modern blocking approaches for entity resolution, focusing on those based upon locality sensitive hashing (LSH). First, we introduce $k$-means locality sensitive hashing (KLSH), which is based upon the information retrieval literature and clusters similar records into blocks using a vector-space representation and projections. Second, we introduce a subquadratic variant of LSH to the literature, known as Densified One Permutation Hashing (DOPH). Third, we propose a weighted variant of DOPH. We illustrate each method on an application to a subset of the ongoing Syrian conflict, giving a discussion of each method.

Posterior Prototyping: Bridging the Gap between Bayesian Record Linkage and Regression

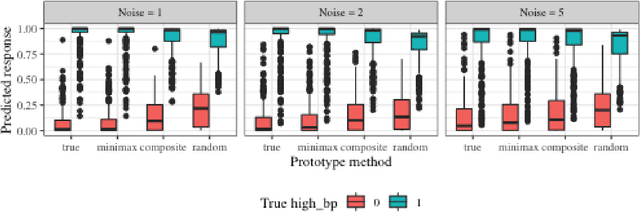
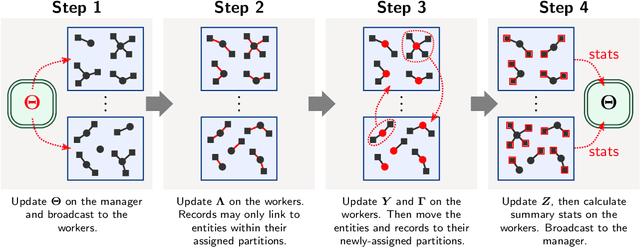
Record linkage (entity resolution or de-deduplication) is the process of merging noisy databases to remove duplicate entities. While record linkage removes duplicate entities from the data, many researchers are interested in performing inference, prediction or post-linkage analysis on the linked data, which we call the downstream task. Depending on the downstream task, one may wish to find the most representative record before performing the post-linkage analysis. Motivated by the downstream task, we propose first performing record linkage using a Bayesian model and then choosing representative records through prototyping. Given the information about the representative records, we then explore two downstream tasks - linear regression and binary classification via logistic regression. In addition, we explore how error propagation occurs in both of these settings. We provide thorough empirical studies for our proposed methodology, and conclude with a discussion of practical insights into our work.

Performance Bounds for Graphical Record Linkage

Record linkage involves merging records in large, noisy databases to remove duplicate entities. It has become an important area because of its widespread occurrence in bibliometrics, public health, official statistics production, political science, and beyond. Traditional linkage methods directly linking records to one another are computationally infeasible as the number of records grows. As a result, it is increasingly common for researchers to treat record linkage as a clustering task, in which each latent entity is associated with one or more noisy database records. We critically assess performance bounds using the Kullback-Leibler (KL) divergence under a Bayesian record linkage framework, making connections to Kolchin partition models. We provide an upper bound using the KL divergence and a lower bound on the minimum probability of misclassifying a latent entity. We give insights for when our bounds hold using simulated data and provide practical user guidance.

Bayesian Learning of Dynamic Multilayer Networks

A plethora of networks is being collected in a growing number of fields, including disease transmission, international relations, social interactions, and others. As data streams continue to grow, the complexity associated with these highly multidimensional connectivity data presents novel challenges. In this paper, we focus on the time-varying interconnections among a set of actors in multiple contexts, called layers. Current literature lacks flexible statistical models for dynamic multilayer networks, which can enhance quality in inference and prediction by efficiently borrowing information within each network, across time, and between layers. Motivated by this gap, we develop a Bayesian nonparametric model leveraging latent space representations. Our formulation characterizes the edge probabilities as a function of shared and layer-specific actors positions in a latent space, with these positions changing in time via Gaussian processes. This representation facilitates dimensionality reduction and incorporates different sources of information in the observed data. In addition, we obtain tractable procedures for posterior computation, inference, and prediction. We provide theoretical results on the flexibility of our model. Our methods are tested on simulations and infection studies monitoring dynamic face-to-face contacts among individuals in multiple days, where we perform better than current methods in inference and prediction.

Flexible Models for Microclustering with Application to Entity Resolution

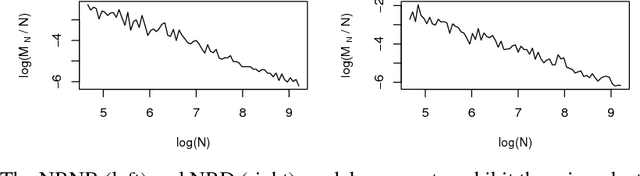
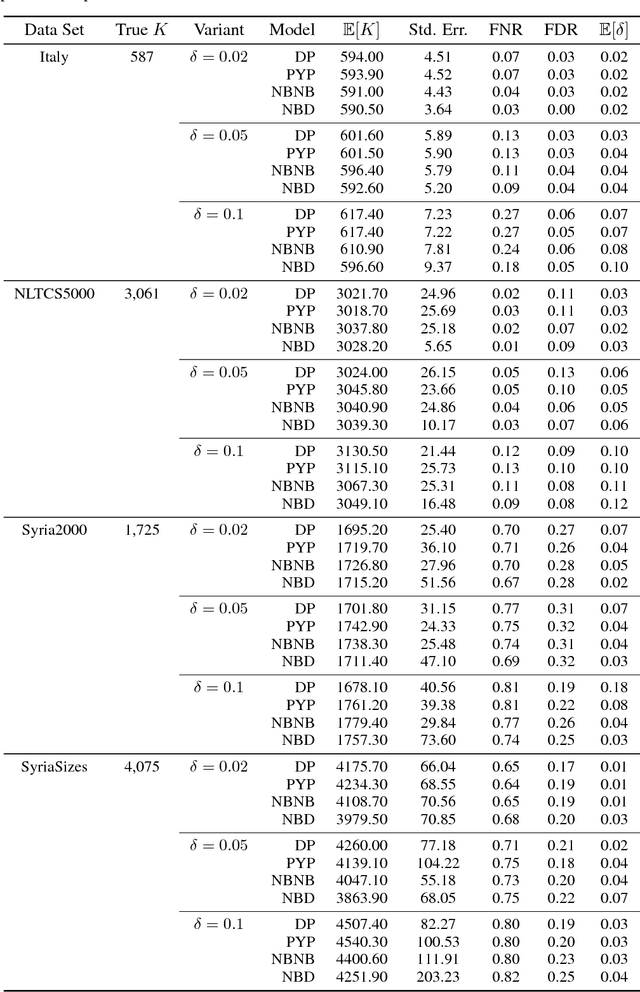
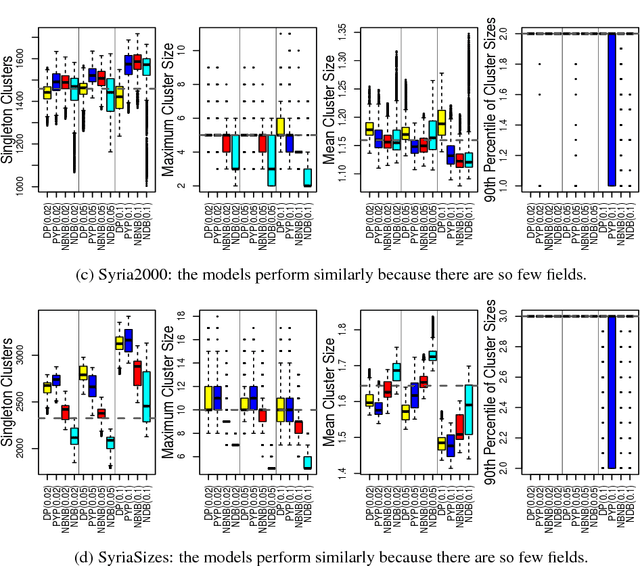
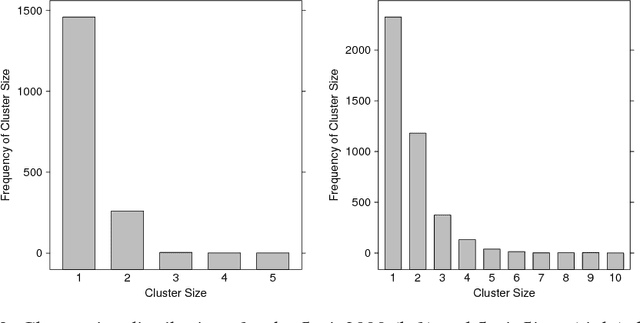
Most generative models for clustering implicitly assume that the number of data points in each cluster grows linearly with the total number of data points. Finite mixture models, Dirichlet process mixture models, and Pitman--Yor process mixture models make this assumption, as do all other infinitely exchangeable clustering models. However, for some applications, this assumption is inappropriate. For example, when performing entity resolution, the size of each cluster should be unrelated to the size of the data set, and each cluster should contain a negligible fraction of the total number of data points. These applications require models that yield clusters whose sizes grow sublinearly with the size of the data set. We address this requirement by defining the microclustering property and introducing a new class of models that can exhibit this property. We compare models within this class to two commonly used clustering models using four entity-resolution data sets.

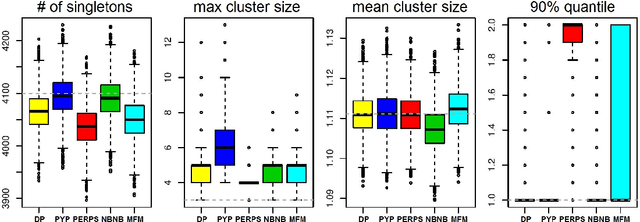
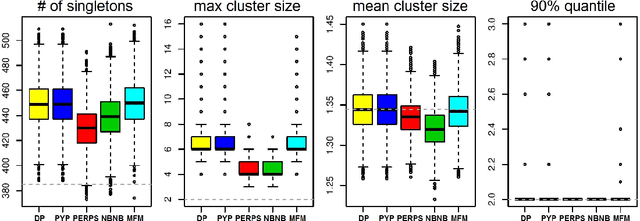
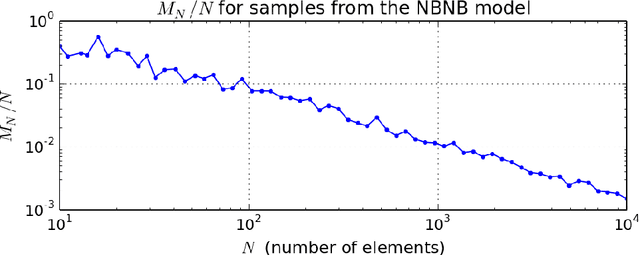
Microclustering: When the Cluster Sizes Grow Sublinearly with the Size of the Data Set

Most generative models for clustering implicitly assume that the number of data points in each cluster grows linearly with the total number of data points. Finite mixture models, Dirichlet process mixture models, and Pitman--Yor process mixture models make this assumption, as do all other infinitely exchangeable clustering models. However, for some tasks, this assumption is undesirable. For example, when performing entity resolution, the size of each cluster is often unrelated to the size of the data set. Consequently, each cluster contains a negligible fraction of the total number of data points. Such tasks therefore require models that yield clusters whose sizes grow sublinearly with the size of the data set. We address this requirement by defining the \emph{microclustering property} and introducing a new model that exhibits this property. We compare this model to several commonly used clustering models by checking model fit using real and simulated data sets.

Variational Bayes for Merging Noisy Databases

Bayesian entity resolution merges together multiple, noisy databases and returns the minimal collection of unique individuals represented, together with their true, latent record values. Bayesian methods allow flexible generative models that share power across databases as well as principled quantification of uncertainty for queries of the final, resolved database. However, existing Bayesian methods for entity resolution use Markov monte Carlo method (MCMC) approximations and are too slow to run on modern databases containing millions or billions of records. Instead, we propose applying variational approximations to allow scalable Bayesian inference in these models. We derive a coordinate-ascent approximation for mean-field variational Bayes, qualitatively compare our algorithm to existing methods, note unique challenges for inference that arise from the expected distribution of cluster sizes in entity resolution, and discuss directions for future work in this domain.