Microclustering: When the Cluster Sizes Grow Sublinearly with the Size of the Data Set
Paper and Code
Dec 02, 2015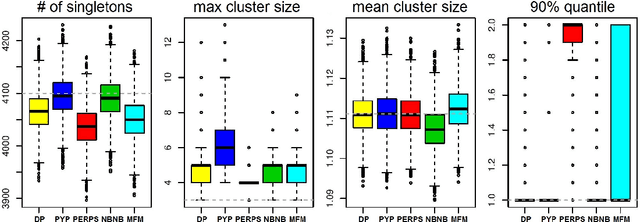
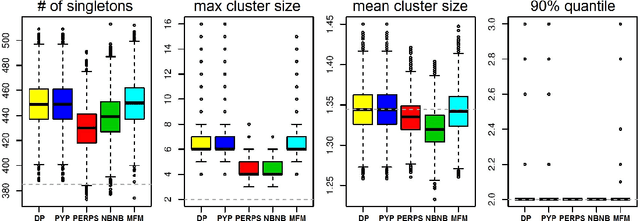
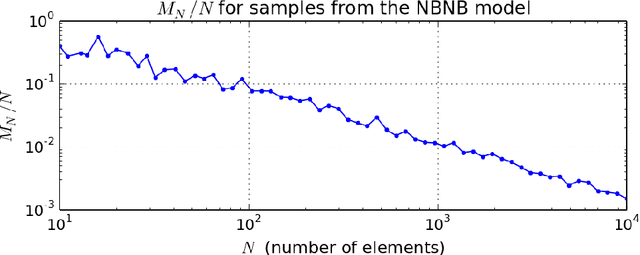
Most generative models for clustering implicitly assume that the number of data points in each cluster grows linearly with the total number of data points. Finite mixture models, Dirichlet process mixture models, and Pitman--Yor process mixture models make this assumption, as do all other infinitely exchangeable clustering models. However, for some tasks, this assumption is undesirable. For example, when performing entity resolution, the size of each cluster is often unrelated to the size of the data set. Consequently, each cluster contains a negligible fraction of the total number of data points. Such tasks therefore require models that yield clusters whose sizes grow sublinearly with the size of the data set. We address this requirement by defining the \emph{microclustering property} and introducing a new model that exhibits this property. We compare this model to several commonly used clustering models by checking model fit using real and simulated data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge