A Latent Space Model for Multilayer Network Data

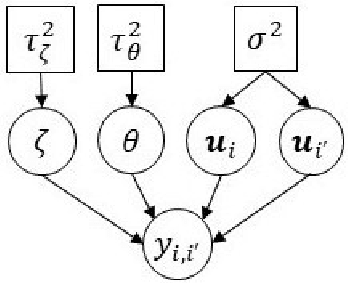
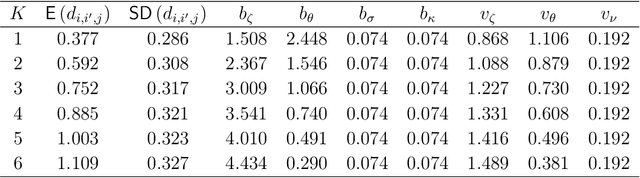
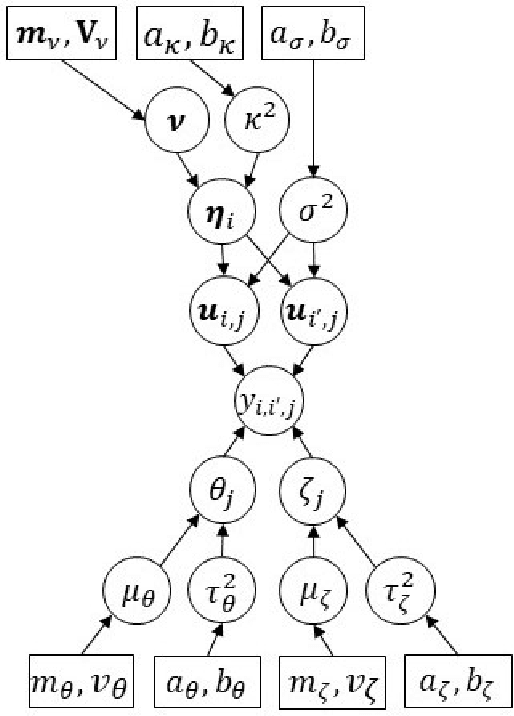
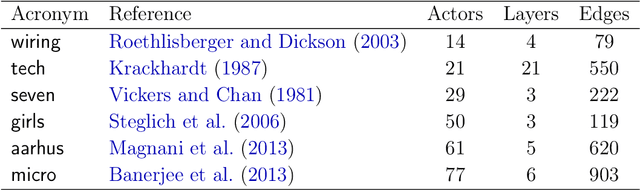
In this work, we propose a Bayesian statistical model to simultaneously characterize two or more social networks defined over a common set of actors. The key feature of the model is a hierarchical prior distribution that allows us to represent the entire system jointly, achieving a compromise between dependent and independent networks. Among others things, such a specification easily allows us to visualize multilayer network data in a low-dimensional Euclidean space, generate a weighted network that reflects the consensus affinity between actors, establish a measure of correlation between networks, assess cognitive judgements that subjects form about the relationships among actors, and perform clustering tasks at different social instances. Our model's capabilities are illustrated using several real-world data sets, taking into account different types of actors, sizes, and relations.

Posterior Prototyping: Bridging the Gap between Bayesian Record Linkage and Regression

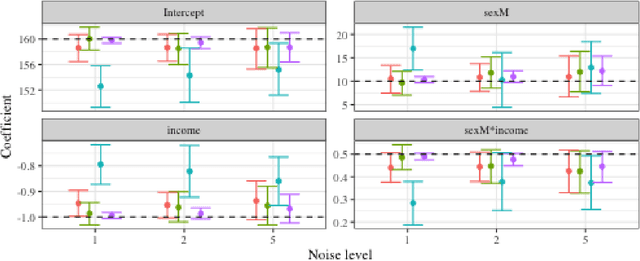
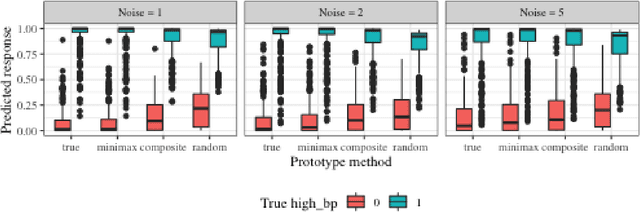
Record linkage (entity resolution or de-deduplication) is the process of merging noisy databases to remove duplicate entities. While record linkage removes duplicate entities from the data, many researchers are interested in performing inference, prediction or post-linkage analysis on the linked data, which we call the downstream task. Depending on the downstream task, one may wish to find the most representative record before performing the post-linkage analysis. Motivated by the downstream task, we propose first performing record linkage using a Bayesian model and then choosing representative records through prototyping. Given the information about the representative records, we then explore two downstream tasks - linear regression and binary classification via logistic regression. In addition, we explore how error propagation occurs in both of these settings. We provide thorough empirical studies for our proposed methodology, and conclude with a discussion of practical insights into our work.

Flexible Models for Microclustering with Application to Entity Resolution

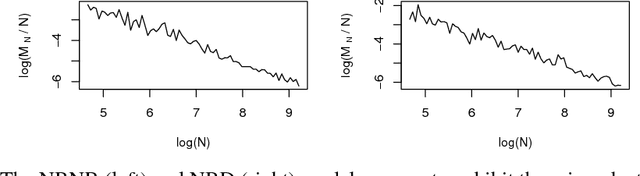
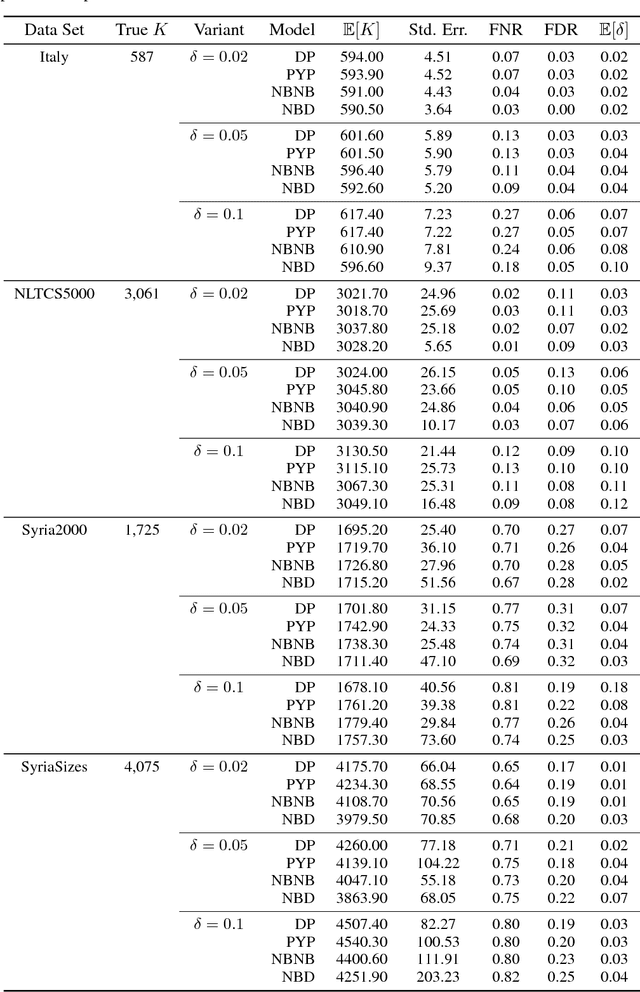
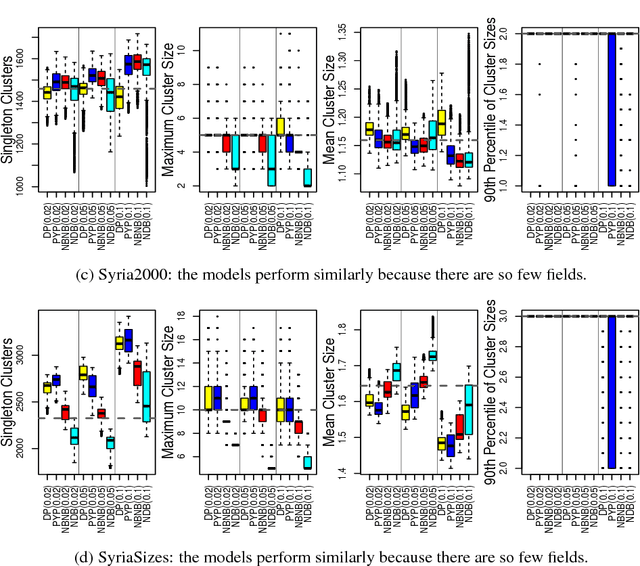
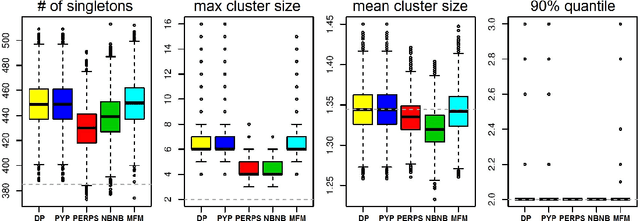
Most generative models for clustering implicitly assume that the number of data points in each cluster grows linearly with the total number of data points. Finite mixture models, Dirichlet process mixture models, and Pitman--Yor process mixture models make this assumption, as do all other infinitely exchangeable clustering models. However, for some applications, this assumption is inappropriate. For example, when performing entity resolution, the size of each cluster should be unrelated to the size of the data set, and each cluster should contain a negligible fraction of the total number of data points. These applications require models that yield clusters whose sizes grow sublinearly with the size of the data set. We address this requirement by defining the microclustering property and introducing a new class of models that can exhibit this property. We compare models within this class to two commonly used clustering models using four entity-resolution data sets.

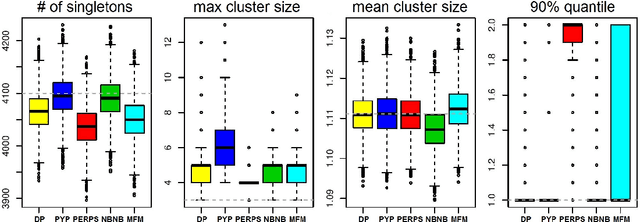
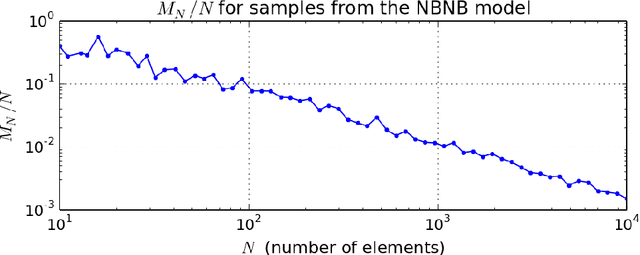
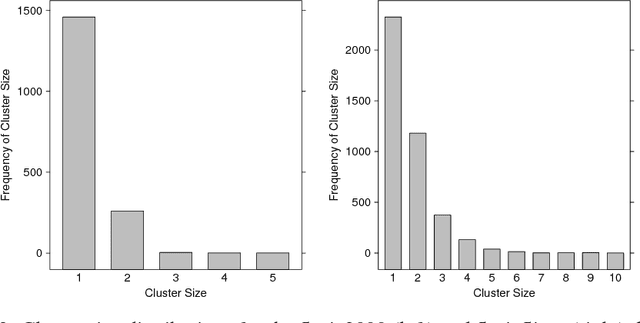
Microclustering: When the Cluster Sizes Grow Sublinearly with the Size of the Data Set

Most generative models for clustering implicitly assume that the number of data points in each cluster grows linearly with the total number of data points. Finite mixture models, Dirichlet process mixture models, and Pitman--Yor process mixture models make this assumption, as do all other infinitely exchangeable clustering models. However, for some tasks, this assumption is undesirable. For example, when performing entity resolution, the size of each cluster is often unrelated to the size of the data set. Consequently, each cluster contains a negligible fraction of the total number of data points. Such tasks therefore require models that yield clusters whose sizes grow sublinearly with the size of the data set. We address this requirement by defining the \emph{microclustering property} and introducing a new model that exhibits this property. We compare this model to several commonly used clustering models by checking model fit using real and simulated data sets.