Complexity of Markov Chain Monte Carlo for Generalized Linear Models

Markov Chain Monte Carlo (MCMC), Laplace approximation (LA) and variational inference (VI) methods are popular approaches to Bayesian inference, each with trade-offs between computational cost and accuracy. However, a theoretical understanding of these differences is missing, particularly when both the sample size $n$ and the dimension $d$ are large. LA and Gaussian VI are justified by Bernstein-von Mises (BvM) theorems, and recent work has derived the characteristic condition $n\gg d^2$ for their validity, improving over the condition $n\gg d^3$. In this paper, we show for linear, logistic and Poisson regression that for $n\gtrsim d$, MCMC attains the same complexity scaling in $n$, $d$ as first-order optimization algorithms, up to sub-polynomial factors. Thus MCMC is competitive with LA and Gaussian VI in complexity, under a scaling between $n$ and $d$ more general than BvM regimes. Our complexities apply to appropriately scaled priors that are not necessarily Gaussian-tailed, including Student-$t$ and flat priors, with log-posteriors that are not necessarily globally concave or gradient-Lipschitz.

Mixing times of data-augmentation Gibbs samplers for high-dimensional probit regression

We investigate the convergence properties of popular data-augmentation samplers for Bayesian probit regression. Leveraging recent results on Gibbs samplers for log-concave targets, we provide simple and explicit non-asymptotic bounds on the associated mixing times (in Kullback-Leibler divergence). The bounds depend explicitly on the design matrix and the prior precision, while they hold uniformly over the vector of responses. We specialize the results for different regimes of statistical interest, when both the number of data points $n$ and parameters $p$ are large: in particular we identify scenarios where the mixing times remain bounded as $n,p\to\infty$, and ones where they do not. The results are shown to be tight (in the worst case with respect to the responses) and provide guidance on choices of prior distributions that provably lead to fast mixing. An empirical analysis based on coupling techniques suggests that the bounds are effective in predicting practically observed behaviours.

Conjugate gradient methods for high-dimensional GLMMs

Generalized linear mixed models (GLMMs) are a widely used tool in statistical analysis. The main bottleneck of many computational approaches lies in the inversion of the high dimensional precision matrices associated with the random effects. Such matrices are typically sparse; however, the sparsity pattern resembles a multi partite random graph, which does not lend itself well to default sparse linear algebra techniques. Notably, we show that, for typical GLMMs, the Cholesky factor is dense even when the original precision is sparse. We thus turn to approximate iterative techniques, in particular to the conjugate gradient (CG) method. We combine a detailed analysis of the spectrum of said precision matrices with results from random graph theory to show that CG-based methods applied to high-dimensional GLMMs typically achieve a fixed approximation error with a total cost that scales linearly with the number of parameters and observations. Numerical illustrations with both real and simulated data confirm the theoretical findings, while at the same time illustrating situations, such as nested structures, where CG-based methods struggle.

Optimal lower bounds for logistic log-likelihoods

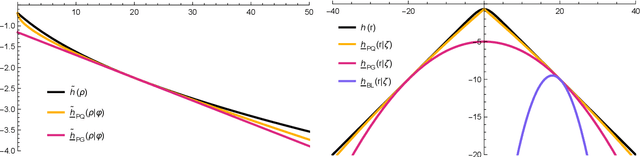
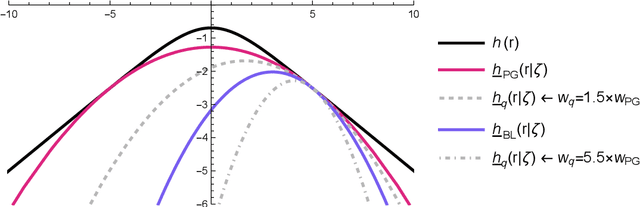
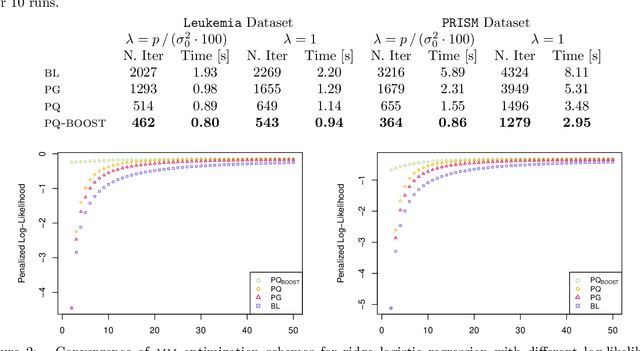
The logit transform is arguably the most widely-employed link function beyond linear settings. This transformation routinely appears in regression models for binary data and provides, either explicitly or implicitly, a core building-block within state-of-the-art methodologies for both classification and regression. Its widespread use, combined with the lack of analytical solutions for the optimization of general losses involving the logit transform, still motivates active research in computational statistics. Among the directions explored, a central one has focused on the design of tangent lower bounds for logistic log-likelihoods that can be tractably optimized, while providing a tight approximation of these log-likelihoods. Although progress along these lines has led to the development of effective minorize-maximize (MM) algorithms for point estimation and coordinate ascent variational inference schemes for approximate Bayesian inference under several logit models, the overarching focus in the literature has been on tangent quadratic minorizers. In fact, it is still unclear whether tangent lower bounds sharper than quadratic ones can be derived without undermining the tractability of the resulting minorizer. This article addresses such a challenging question through the design and study of a novel piece-wise quadratic lower bound that uniformly improves any tangent quadratic minorizer, including the sharpest ones, while admitting a direct interpretation in terms of the classical generalized lasso problem. As illustrated in a ridge logistic regression, this unique connection facilitates more effective implementations than those provided by available piece-wise bounds, while improving the convergence speed of quadratic ones.

Linear-cost unbiased posterior estimates for crossed effects and matrix factorization models via couplings

We design and analyze unbiased Markov chain Monte Carlo (MCMC) schemes based on couplings of blocked Gibbs samplers (BGSs), whose total computational costs scale linearly with the number of parameters and data points. Our methodology is designed for and applicable to high-dimensional BGS with conditionally independent blocks, which are often encountered in Bayesian modeling. We provide bounds on the expected number of iterations needed for coalescence for Gaussian targets, which imply that practical two-step coupling strategies achieve coalescence times that match the relaxation times of the original BGS scheme up to a logarithmic factor. To illustrate the practical relevance of our methodology, we apply it to high-dimensional crossed random effect and probabilistic matrix factorization models, for which we develop a novel BGS scheme with improved convergence speed. Our methodology provides unbiased posterior estimates at linear cost (usually requiring only a few BGS iterations for problems with thousands of parameters), matching state-of-the-art procedures for both frequentist and Bayesian estimation of those models.

Entropy contraction of the Gibbs sampler under log-concavity

The Gibbs sampler (a.k.a. Glauber dynamics and heat-bath algorithm) is a popular Markov Chain Monte Carlo algorithm which iteratively samples from the conditional distributions of a probability measure $\pi$ of interest. Under the assumption that $\pi$ is strongly log-concave, we show that the random scan Gibbs sampler contracts in relative entropy and provide a sharp characterization of the associated contraction rate. Assuming that evaluating conditionals is cheap compared to evaluating the joint density, our results imply that the number of full evaluations of $\pi$ needed for the Gibbs sampler to mix grows linearly with the condition number and is independent of the dimension. If $\pi$ is non-strongly log-concave, the convergence rate in entropy degrades from exponential to polynomial. Our techniques are versatile and extend to Metropolis-within-Gibbs schemes and the Hit-and-Run algorithm. A comparison with gradient-based schemes and the connection with the optimization literature are also discussed.

Convergence rate of random scan Coordinate Ascent Variational Inference under log-concavity

The Coordinate Ascent Variational Inference scheme is a popular algorithm used to compute the mean-field approximation of a probability distribution of interest. We analyze its random scan version, under log-concavity assumptions on the target density. Our approach builds on the recent work of M. Arnese and D. Lacker, \emph{Convergence of coordinate ascent variational inference for log-concave measures via optimal transport} [arXiv:2404.08792] which studies the deterministic scan version of the algorithm, phrasing it as a block-coordinate descent algorithm in the space of probability distributions endowed with the geometry of optimal transport. We obtain tight rates for the random scan version, which imply that the total number of factor updates required to converge scales linearly with the condition number and the number of blocks of the target distribution. By contrast, available bounds for the deterministic scan case scale quadratically in the same quantities, which is analogue to what happens for optimization of convex functions in Euclidean spaces.

Robust Approximate Sampling via Stochastic Gradient Barker Dynamics

Stochastic Gradient (SG) Markov Chain Monte Carlo algorithms (MCMC) are popular algorithms for Bayesian sampling in the presence of large datasets. However, they come with little theoretical guarantees and assessing their empirical performances is non-trivial. In such context, it is crucial to develop algorithms that are robust to the choice of hyperparameters and to gradients heterogeneity since, in practice, both the choice of step-size and behaviour of target gradients induce hard-to-control biases in the invariant distribution. In this work we introduce the stochastic gradient Barker dynamics (SGBD) algorithm, extending the recently developed Barker MCMC scheme, a robust alternative to Langevin-based sampling algorithms, to the stochastic gradient framework. We characterize the impact of stochastic gradients on the Barker transition mechanism and develop a bias-corrected version that, under suitable assumptions, eliminates the error due to the gradient noise in the proposal. We illustrate the performance on a number of high-dimensional examples, showing that SGBD is more robust to hyperparameter tuning and to irregular behavior of the target gradients compared to the popular stochastic gradient Langevin dynamics algorithm.

Scalability of Metropolis-within-Gibbs schemes for high-dimensional Bayesian models

We study general coordinate-wise MCMC schemes (such as Metropolis-within-Gibbs samplers), which are commonly used to fit Bayesian non-conjugate hierarchical models. We relate their convergence properties to the ones of the corresponding (potentially not implementable) Gibbs sampler through the notion of conditional conductance. This allows us to study the performances of popular Metropolis-within-Gibbs schemes for non-conjugate hierarchical models, in high-dimensional regimes where both number of datapoints and parameters increase. Given random data-generating assumptions, we establish dimension-free convergence results, which are in close accordance with numerical evidences. Applications to Bayesian models for binary regression with unknown hyperparameters and discretely observed diffusions are also discussed. Motivated by such statistical applications, auxiliary results of independent interest on approximate conductances and perturbation of Markov operators are provided.

Partially factorized variational inference for high-dimensional mixed models

While generalized linear mixed models (GLMMs) are a fundamental tool in applied statistics, many specifications -- such as those involving categorical factors with many levels or interaction terms -- can be computationally challenging to estimate due to the need to compute or approximate high-dimensional integrals. Variational inference (VI) methods are a popular way to perform such computations, especially in the Bayesian context. However, naive VI methods can provide unreliable uncertainty quantification. We show that this is indeed the case in the GLMM context, proving that standard VI (i.e. mean-field) dramatically underestimates posterior uncertainty in high-dimensions. We then show how appropriately relaxing the mean-field assumption leads to VI methods whose uncertainty quantification does not deteriorate in high-dimensions, and whose total computational cost scales linearly with the number of parameters and observations. Our theoretical and numerical results focus on GLMMs with Gaussian or binomial likelihoods, and rely on connections to random graph theory to obtain sharp high-dimensional asymptotic analysis. We also provide generic results, which are of independent interest, relating the accuracy of variational inference to the convergence rate of the corresponding coordinate ascent variational inference (CAVI) algorithm for Gaussian targets. Our proposed partially-factorized VI (PF-VI) methodology for GLMMs is implemented in the R package vglmer, see https://github.com/mgoplerud/vglmer . Numerical results with simulated and real data examples illustrate the favourable computation cost versus accuracy trade-off of PF-VI.