Differential privacy guarantees of Markov chain Monte Carlo algorithms

This paper aims to provide differential privacy (DP) guarantees for Markov chain Monte Carlo (MCMC) algorithms. In a first part, we establish DP guarantees on samples output by MCMC algorithms as well as Monte Carlo estimators associated with these methods under assumptions on the convergence properties of the underlying Markov chain. In particular, our results highlight the critical condition of ensuring the target distribution is differentially private itself. In a second part, we specialise our analysis to the unadjusted Langevin algorithm and stochastic gradient Langevin dynamics and establish guarantees on their (R\'enyi) DP. To this end, we develop a novel methodology based on Girsanov's theorem combined with a perturbation trick to obtain bounds for an unbounded domain and in a non-convex setting. We establish: (i) uniform in $n$ privacy guarantees when the state of the chain after $n$ iterations is released, (ii) bounds on the privacy of the entire chain trajectory. These findings provide concrete guidelines for privacy-preserving MCMC.

Stochastic Gradient Piecewise Deterministic Monte Carlo Samplers

Recent work has suggested using Monte Carlo methods based on piecewise deterministic Markov processes (PDMPs) to sample from target distributions of interest. PDMPs are non-reversible continuous-time processes endowed with momentum, and hence can mix better than standard reversible MCMC samplers. Furthermore, they can incorporate exact sub-sampling schemes which only require access to a single (randomly selected) data point at each iteration, yet without introducing bias to the algorithm's stationary distribution. However, the range of models for which PDMPs can be used, particularly with sub-sampling, is limited. We propose approximate simulation of PDMPs with sub-sampling for scalable sampling from posterior distributions. The approximation takes the form of an Euler approximation to the true PDMP dynamics, and involves using an estimate of the gradient of the log-posterior based on a data sub-sample. We thus call this class of algorithms stochastic-gradient PDMPs. Importantly, the trajectories of stochastic-gradient PDMPs are continuous and can leverage recent ideas for sampling from measures with continuous and atomic components. We show these methods are easy to implement, present results on their approximation error and demonstrate numerically that this class of algorithms has similar efficiency to, but is more robust than, stochastic gradient Langevin dynamics.

Scalability of Metropolis-within-Gibbs schemes for high-dimensional Bayesian models

We study general coordinate-wise MCMC schemes (such as Metropolis-within-Gibbs samplers), which are commonly used to fit Bayesian non-conjugate hierarchical models. We relate their convergence properties to the ones of the corresponding (potentially not implementable) Gibbs sampler through the notion of conditional conductance. This allows us to study the performances of popular Metropolis-within-Gibbs schemes for non-conjugate hierarchical models, in high-dimensional regimes where both number of datapoints and parameters increase. Given random data-generating assumptions, we establish dimension-free convergence results, which are in close accordance with numerical evidences. Applications to Bayesian models for binary regression with unknown hyperparameters and discretely observed diffusions are also discussed. Motivated by such statistical applications, auxiliary results of independent interest on approximate conductances and perturbation of Markov operators are provided.

Stereographic Markov Chain Monte Carlo

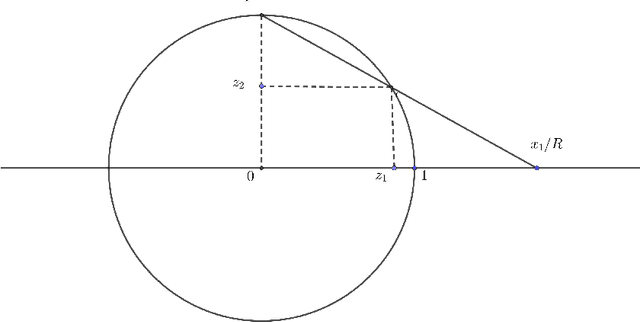
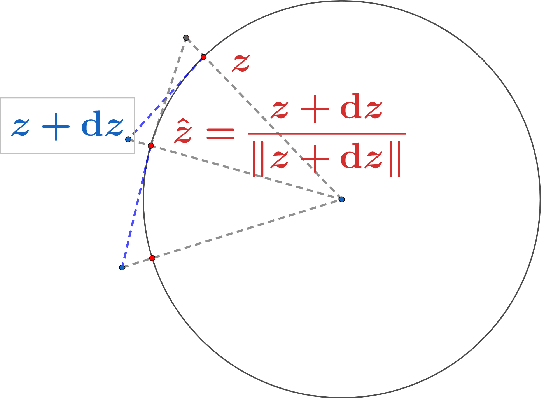
High dimensional distributions, especially those with heavy tails, are notoriously difficult for off-the-shelf MCMC samplers: the combination of unbounded state spaces, diminishing gradient information, and local moves, results in empirically observed "stickiness" and poor theoretical mixing properties -- lack of geometric ergodicity. In this paper, we introduce a new class of MCMC samplers that map the original high dimensional problem in Euclidean space onto a sphere and remedy these notorious mixing problems. In particular, we develop random-walk Metropolis type algorithms as well as versions of Bouncy Particle Sampler that are uniformly ergodic for a large class of light and heavy-tailed distributions and also empirically exhibit rapid convergence in high dimensions. In the best scenario, the proposed samplers can enjoy the ``blessings of dimensionality'' that the mixing time decreases with dimension.

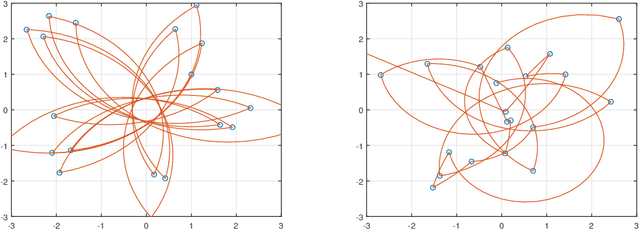
Divide-and-Conquer Monte Carlo Fusion

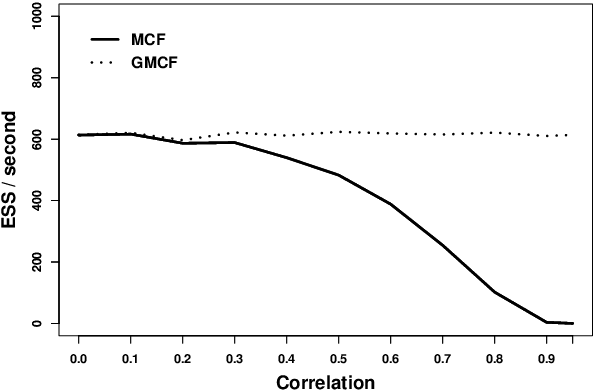
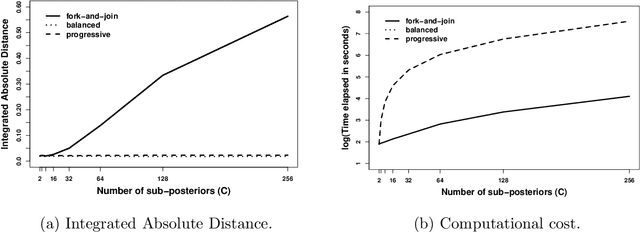
Combining several (sample approximations of) distributions, which we term sub-posteriors, into a single distribution proportional to their product, is a common challenge. For instance, in distributed `big data' problems, or when working under multi-party privacy constraints. Many existing approaches resort to approximating the individual sub-posteriors for practical necessity, then representing the resulting approximate posterior. The quality of the posterior approximation for these approaches is poor when the sub-posteriors fall out-with a narrow range of distributional form. Recently, a Fusion approach has been proposed which finds a direct and exact Monte Carlo approximation of the posterior (as opposed to the sub-posteriors), circumventing the drawbacks of approximate approaches. Unfortunately, existing Fusion approaches have a number of computational limitations, particularly when unifying a large number of sub-posteriors. In this paper, we generalise the theory underpinning existing Fusion approaches, and embed the resulting methodology within a recursive divide-and-conquer sequential Monte Carlo paradigm. This ultimately leads to a competitive Fusion approach, which is robust to increasing numbers of sub-posteriors.

Scalable inference for crossed random effects models

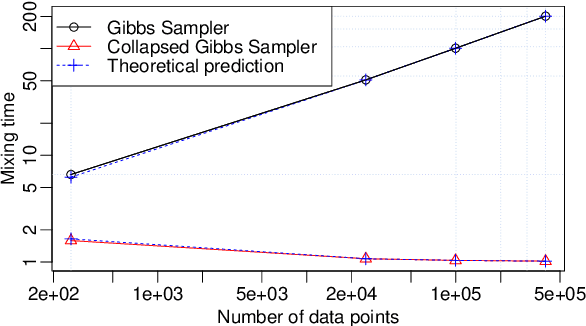
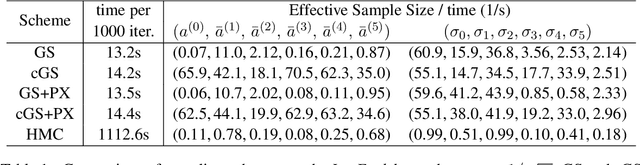
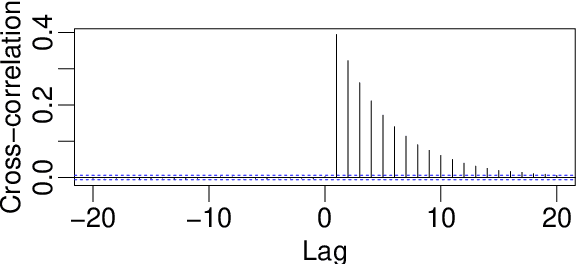
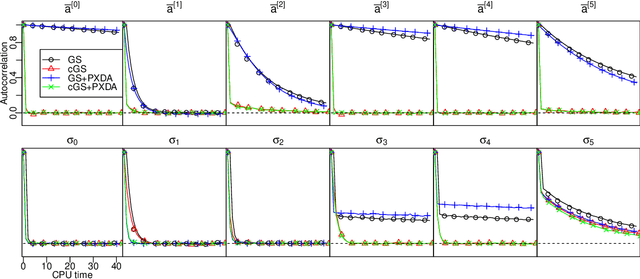
We analyze the complexity of Gibbs samplers for inference in crossed random effect models used in modern analysis of variance. We demonstrate that for certain designs the plain vanilla Gibbs sampler is not scalable, in the sense that its complexity is worse than proportional to the number of parameters and data. We thus propose a simple modification leading to a collapsed Gibbs sampler that is provably scalable. Although our theory requires some balancedness assumptions on the data designs, we demonstrate in simulated and real datasets that the rates it predicts match remarkably the correct rates in cases where the assumptions are violated. We also show that the collapsed Gibbs sampler, extended to sample further unknown hyperparameters, outperforms significantly alternative state of the art algorithms.