Redesigning the ensemble Kalman filter with a dedicated model of epistemic uncertainty

The problem of incorporating information from observations received serially in time is widespread in the field of uncertainty quantification. Within a probabilistic framework, such problems can be addressed using standard filtering techniques. However, in many real-world problems, some (or all) of the uncertainty is epistemic, arising from a lack of knowledge, and is difficult to model probabilistically. This paper introduces a possibilistic ensemble Kalman filter designed for this setting and characterizes some of its properties. Using possibility theory to describe epistemic uncertainty is appealing from a philosophical perspective, and it is easy to justify certain heuristics often employed in standard ensemble Kalman filters as principled approaches to capturing uncertainty within it. The possibilistic approach motivates a robust mechanism for characterizing uncertainty which shows good performance with small sample sizes, and can outperform standard ensemble Kalman filters at given sample size, even when dealing with genuinely aleatoric uncertainty.

Particle Semi-Implicit Variational Inference

Semi-implicit variational inference (SIVI) enriches the expressiveness of variational families by utilizing a kernel and a mixing distribution to hierarchically define the variational distribution. Existing SIVI methods parameterize the mixing distribution using implicit distributions, leading to intractable variational densities. As a result, directly maximizing the evidence lower bound (ELBO) is not possible and so, they resort to either: optimizing bounds on the ELBO, employing costly inner-loop Markov chain Monte Carlo runs, or solving minimax objectives. In this paper, we propose a novel method for SIVI called Particle Variational Inference (PVI) which employs empirical measures to approximate the optimal mixing distributions characterized as the minimizer of a natural free energy functional via a particle approximation of an Euclidean--Wasserstein gradient flow. This approach means that, unlike prior works, PVI can directly optimize the ELBO; furthermore, it makes no parametric assumption about the mixing distribution. Our empirical results demonstrate that PVI performs favourably against other SIVI methods across various tasks. Moreover, we provide a theoretical analysis of the behaviour of the gradient flow of a related free energy functional: establishing the existence and uniqueness of solutions as well as propagation of chaos results.

Error bounds for particle gradient descent, and extensions of the log-Sobolev and Talagrand inequalities

We prove non-asymptotic error bounds for particle gradient descent (PGD)~(Kuntz et al., 2023), a recently introduced algorithm for maximum likelihood estimation of large latent variable models obtained by discretizing a gradient flow of the free energy. We begin by showing that, for models satisfying a condition generalizing both the log-Sobolev and the Polyak--{\L}ojasiewicz inequalities (LSI and P{\L}I, respectively), the flow converges exponentially fast to the set of minimizers of the free energy. We achieve this by extending a result well-known in the optimal transport literature (that the LSI implies the Talagrand inequality) and its counterpart in the optimization literature (that the P{\L}I implies the so-called quadratic growth condition), and applying it to our new setting. We also generalize the Bakry--\'Emery Theorem and show that the LSI/P{\L}I generalization holds for models with strongly concave log-likelihoods. For such models, we further control PGD's discretization error, obtaining non-asymptotic error bounds. While we are motivated by the study of PGD, we believe that the inequalities and results we extend may be of independent interest.

Momentum Particle Maximum Likelihood

Maximum likelihood estimation (MLE) of latent variable models is often recast as an optimization problem over the extended space of parameters and probability distributions. For example, the Expectation Maximization (EM) algorithm can be interpreted as coordinate descent applied to a suitable free energy functional over this space. Recently, this perspective has been combined with insights from optimal transport and Wasserstein gradient flows to develop particle-based algorithms applicable to wider classes of models than standard EM. Drawing inspiration from prior works which interpret `momentum-enriched' optimisation algorithms as discretizations of ordinary differential equations, we propose an analogous dynamical systems-inspired approach to minimizing the free energy functional over the extended space of parameters and probability distributions. The result is a dynamic system that blends elements of Nesterov's Accelerated Gradient method, the underdamped Langevin diffusion, and particle methods. Under suitable assumptions, we establish quantitative convergence of the proposed system to the unique minimiser of the functional in continuous time. We then propose a numerical discretization of this system which enables its application to parameter estimation in latent variable models. Through numerical experiments, we demonstrate that the resulting algorithm converges faster than existing methods and compares favourably with other (approximate) MLE algorithms.

Scalable particle-based alternatives to EM

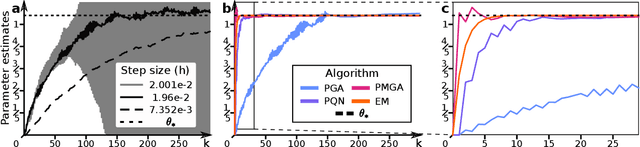
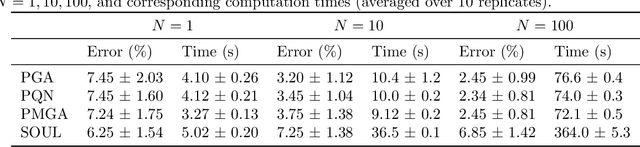
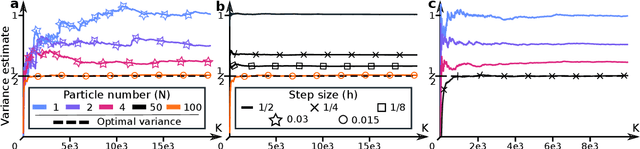
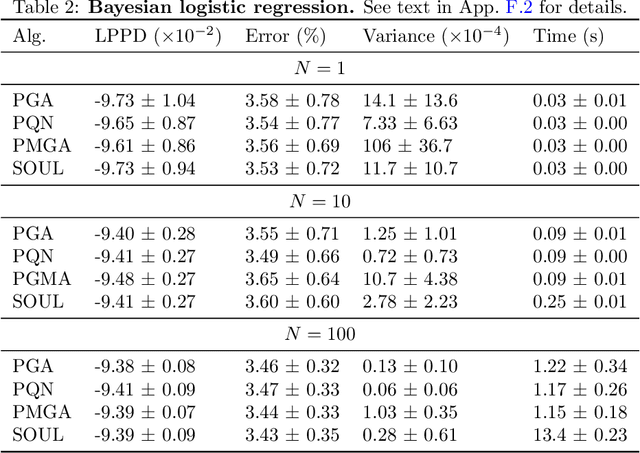
Building on (Neal and Hinton, 1998), where the problem tackled by EM is recast as the optimization of a free energy functional on an infinite-dimensional space, we obtain three practical particle-based alternatives to EM applicable to broad classes of models. All three are derived through straightforward discretizations of gradient flows associated with the functional. The novel algorithms scale well to high-dimensional settings and outperform existing state-of-the-art methods in numerical experiments.

Divide-and-Conquer Monte Carlo Fusion

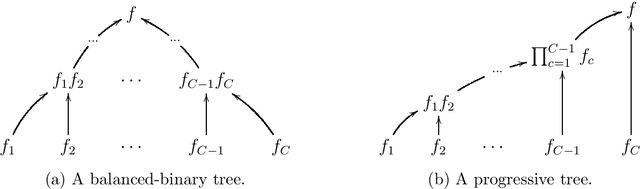
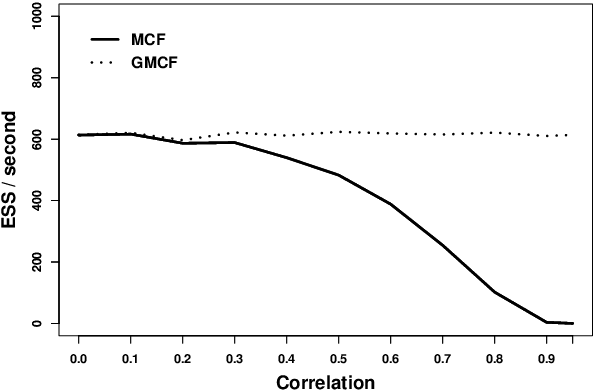
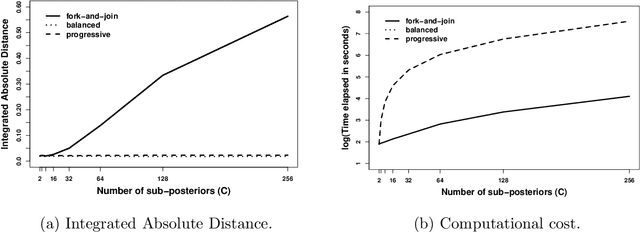
Combining several (sample approximations of) distributions, which we term sub-posteriors, into a single distribution proportional to their product, is a common challenge. For instance, in distributed `big data' problems, or when working under multi-party privacy constraints. Many existing approaches resort to approximating the individual sub-posteriors for practical necessity, then representing the resulting approximate posterior. The quality of the posterior approximation for these approaches is poor when the sub-posteriors fall out-with a narrow range of distributional form. Recently, a Fusion approach has been proposed which finds a direct and exact Monte Carlo approximation of the posterior (as opposed to the sub-posteriors), circumventing the drawbacks of approximate approaches. Unfortunately, existing Fusion approaches have a number of computational limitations, particularly when unifying a large number of sub-posteriors. In this paper, we generalise the theory underpinning existing Fusion approaches, and embed the resulting methodology within a recursive divide-and-conquer sequential Monte Carlo paradigm. This ultimately leads to a competitive Fusion approach, which is robust to increasing numbers of sub-posteriors.

Bayesian model comparison with un-normalised likelihoods

Models for which the likelihood function can be evaluated only up to a parameter-dependent unknown normalising constant, such as Markov random field models, are used widely in computer science, statistical physics, spatial statistics, and network analysis. However, Bayesian analysis of these models using standard Monte Carlo methods is not possible due to the intractability of their likelihood functions. Several methods that permit exact, or close to exact, simulation from the posterior distribution have recently been developed. However, estimating the evidence and Bayes' factors (BFs) for these models remains challenging in general. This paper describes new random weight importance sampling and sequential Monte Carlo methods for estimating BFs that use simulation to circumvent the evaluation of the intractable likelihood, and compares them to existing methods. In some cases we observe an advantage in the use of biased weight estimates. An initial investigation into the theoretical and empirical properties of this class of methods is presented. Some support for the use of biased estimates is presented, but we advocate caution in the use of such estimates.

Divide-and-Conquer with Sequential Monte Carlo

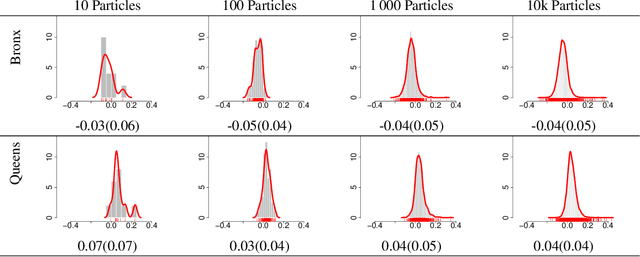
We propose a novel class of Sequential Monte Carlo (SMC) algorithms, appropriate for inference in probabilistic graphical models. This class of algorithms adopts a divide-and-conquer approach based upon an auxiliary tree-structured decomposition of the model of interest, turning the overall inferential task into a collection of recursively solved sub-problems. The proposed method is applicable to a broad class of probabilistic graphical models, including models with loops. Unlike a standard SMC sampler, the proposed Divide-and-Conquer SMC employs multiple independent populations of weighted particles, which are resampled, merged, and propagated as the method progresses. We illustrate empirically that this approach can outperform standard methods in terms of the accuracy of the posterior expectation and marginal likelihood approximations. Divide-and-Conquer SMC also opens up novel parallel implementation options and the possibility of concentrating the computational effort on the most challenging sub-problems. We demonstrate its performance on a Markov random field and on a hierarchical logistic regression problem.