Forward-only Diffusion Probabilistic Models

This work presents a forward-only diffusion (FoD) approach for generative modelling. In contrast to traditional diffusion models that rely on a coupled forward-backward diffusion scheme, FoD directly learns data generation through a single forward diffusion process, yielding a simple yet efficient generative framework. The core of FoD is a state-dependent linear stochastic differential equation that involves a mean-reverting term in both the drift and diffusion functions. This mean-reversion property guarantees the convergence to clean data, naturally simulating a stochastic interpolation between source and target distributions. More importantly, FoD is analytically tractable and is trained using a simple stochastic flow matching objective, enabling a few-step non-Markov chain sampling during inference. The proposed FoD model, despite its simplicity, achieves competitive performance on various image-conditioned (e.g., image restoration) and unconditional generation tasks, demonstrating its effectiveness in generative modelling. Our code is available at https://github.com/Algolzw/FoD.

Supervised Models Can Generalize Also When Trained on Random Label

The success of unsupervised learning raises the question of whether also supervised models can be trained without using the information in the output $y$. In this paper, we demonstrate that this is indeed possible. The key step is to formulate the model as a smoother, i.e. on the form $\hat{f}=Sy$, and to construct the smoother matrix $S$ independently of $y$, e.g. by training on random labels. We present a simple model selection criterion based on the distribution of the out-of-sample predictions and show that, in contrast to cross-validation, this criterion can be used also without access to $y$. We demonstrate on real and synthetic data that $y$-free trained versions of linear and kernel ridge regression, smoothing splines, and neural networks perform similarly to their standard, $y$-based, versions and, most importantly, significantly better than random guessing.

Safe exploration in reproducing kernel Hilbert spaces

Popular safe Bayesian optimization (BO) algorithms learn control policies for safety-critical systems in unknown environments. However, most algorithms make a smoothness assumption, which is encoded by a known bounded norm in a reproducing kernel Hilbert space (RKHS). The RKHS is a potentially infinite-dimensional space, and it remains unclear how to reliably obtain the RKHS norm of an unknown function. In this work, we propose a safe BO algorithm capable of estimating the RKHS norm from data. We provide statistical guarantees on the RKHS norm estimation, integrate the estimated RKHS norm into existing confidence intervals and show that we retain theoretical guarantees, and prove safety of the resulting safe BO algorithm. We apply our algorithm to safely optimize reinforcement learning policies on physics simulators and on a real inverted pendulum, demonstrating improved performance, safety, and scalability compared to the state-of-the-art.

Probabilistic Bubble Roadmap

Finding a collision-free path is a fundamental problem in robotics, where the sampling based planners have a long line of success. However, this approach is computationally expensive, due to the frequent use of collision-detection. Furthermore, the produced paths are usually jagged and require further post-processing before they can be tracked. Due to their high computational cost, these planners are usually restricted to static settings, since they are not able to cope with rapid changes in the environment. In our work, we remove this restriction by introducing a learned signed distance function expressed in the configuration space of the robot. The signed distance allows us to form collision-free spherical regions in the configuration space, which we use to suggest a new multi-query path planner that also works in dynamic settings. We propose the probabilistic bubble roadmap planner, which enhances the probabilistic roadmap planner (PRM) by using spheres as vertices and compute the edges by checking for neighboring spheres which intersect. We benchmark our approach in a static setting where we show that we can produce paths that are shorter than the paths produced by the PRM, while having a smaller sized roadmap and finding the paths faster. Finally, we show that we can rapidly rewire the graph in the case of new obstacles introduced at run time and therefore produce paths in the case of moving obstacles.

Efficient Optimization Algorithms for Linear Adversarial Training

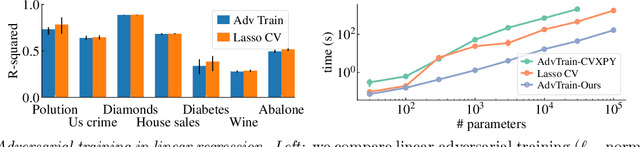
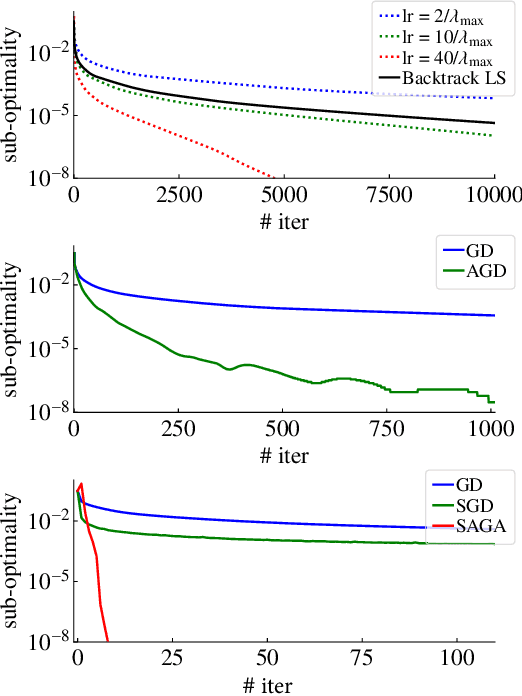
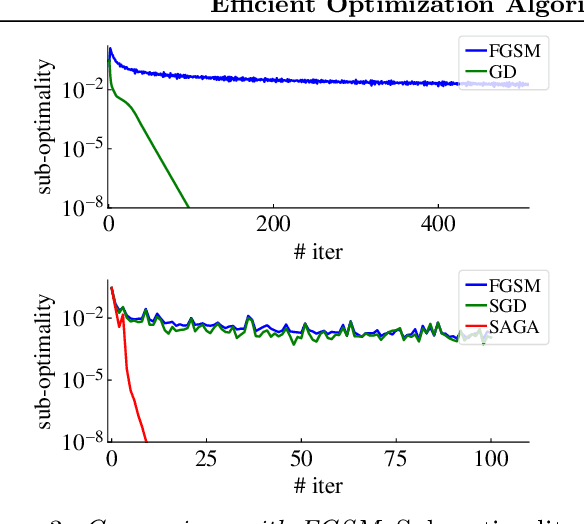
Adversarial training can be used to learn models that are robust against perturbations. For linear models, it can be formulated as a convex optimization problem. Compared to methods proposed in the context of deep learning, leveraging the optimization structure allows significantly faster convergence rates. Still, the use of generic convex solvers can be inefficient for large-scale problems. Here, we propose tailored optimization algorithms for the adversarial training of linear models, which render large-scale regression and classification problems more tractable. For regression problems, we propose a family of solvers based on iterative ridge regression and, for classification, a family of solvers based on projected gradient descent. The methods are based on extended variable reformulations of the original problem. We illustrate their efficiency in numerical examples.

Taming Diffusion Models for Image Restoration: A Review

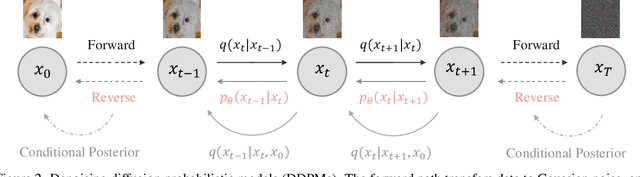
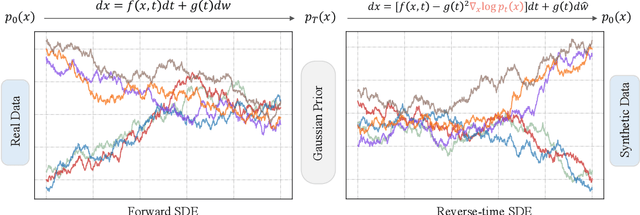
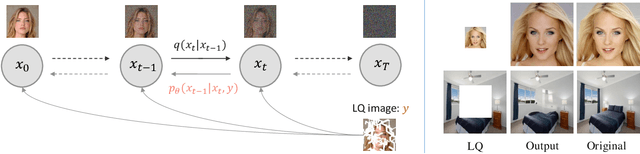
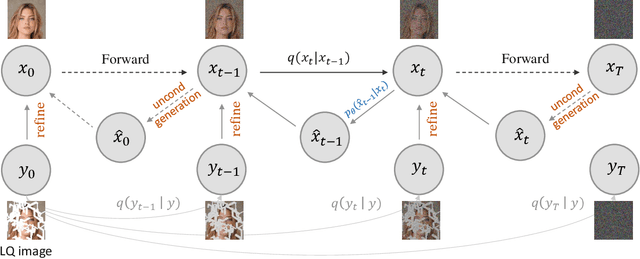
Diffusion models have achieved remarkable progress in generative modelling, particularly in enhancing image quality to conform to human preferences. Recently, these models have also been applied to low-level computer vision for photo-realistic image restoration (IR) in tasks such as image denoising, deblurring, dehazing, etc. In this review paper, we introduce key constructions in diffusion models and survey contemporary techniques that make use of diffusion models in solving general IR tasks. Furthermore, we point out the main challenges and limitations of existing diffusion-based IR frameworks and provide potential directions for future work.

Conditional sampling within generative diffusion models

Generative diffusions are a powerful class of Monte Carlo samplers that leverage bridging Markov processes to approximate complex, high-dimensional distributions, such as those found in image processing and language models. Despite their success in these domains, an important open challenge remains: extending these techniques to sample from conditional distributions, as required in, for example, Bayesian inverse problems. In this paper, we present a comprehensive review of existing computational approaches to conditional sampling within generative diffusion models. Specifically, we highlight key methodologies that either utilise the joint distribution, or rely on (pre-trained) marginal distributions with explicit likelihoods, to construct conditional generative samplers.

Hallucination Detection in LLMs: Fast and Memory-Efficient Finetuned Models

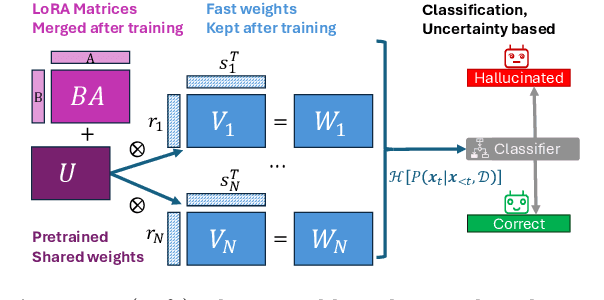
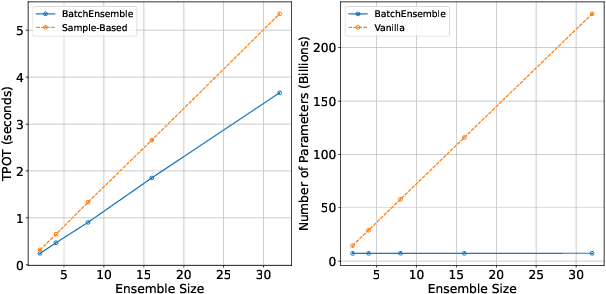
Uncertainty estimation is a necessary component when implementing AI in high-risk settings, such as autonomous cars, medicine, or insurances. Large Language Models (LLMs) have seen a surge in popularity in recent years, but they are subject to hallucinations, which may cause serious harm in high-risk settings. Despite their success, LLMs are expensive to train and run: they need a large amount of computations and memory, preventing the use of ensembling methods in practice. In this work, we present a novel method that allows for fast and memory-friendly training of LLM ensembles. We show that the resulting ensembles can detect hallucinations and are a viable approach in practice as only one GPU is needed for training and inference.

PACSBO: Probably approximately correct safe Bayesian optimization

Safe Bayesian optimization (BO) algorithms promise to find optimal control policies without knowing the system dynamics while at the same time guaranteeing safety with high probability. In exchange for those guarantees, popular algorithms require a smoothness assumption: a known upper bound on a norm in a reproducing kernel Hilbert space (RKHS). The RKHS is a potentially infinite-dimensional space, and it is unclear how to, in practice, obtain an upper bound of an unknown function in its corresponding RKHS. In response, we propose an algorithm that estimates an upper bound on the RKHS norm of an unknown function from data and investigate its theoretical properties. Moreover, akin to Lipschitz-based methods, we treat the RKHS norm as a local rather than a global object, and thus reduce conservatism. Integrating the RKHS norm estimation and the local interpretation of the RKHS norm into a safe BO algorithm yields PACSBO, an algorithm for probably approximately correct safe Bayesian optimization, for which we provide numerical and hardware experiments that demonstrate its applicability and benefits over popular safe BO algorithms.

Accounts of using the Tustin-Net architecture on a rotary inverted pendulum

In this report we investigate the use of the Tustin neural network architecture (Tustin-Net) for the identification of a physical rotary inverse pendulum. This physics-based architecture is of particular interest as it builds on the known relationship between velocities and positions. We here aim at discussing the advantages, limitations and performance of Tustin-Nets compared to first-principles grey-box models on a real physical apparatus, showing how, with a standard training procedure, the former can hardly achieve the same accuracy as the latter. To address this limitation, we present a training strategy based on transfer learning that yields Tustin-Nets that are competitive with the first-principles model, without requiring extensive knowledge of the setup as the latter.