Online learning in motion modeling for intra-interventional image sequences

Image monitoring and guidance during medical examinations can aid both diagnosis and treatment. However, the sampling frequency is often too low, which creates a need to estimate the missing images. We present a probabilistic motion model for sequential medical images, with the ability to both estimate motion between acquired images and forecast the motion ahead of time. The core is a low-dimensional temporal process based on a linear Gaussian state-space model with analytically tractable solutions for forecasting, simulation, and imputation of missing samples. The results, from two experiments on publicly available cardiac datasets, show reliable motion estimates and an improved forecasting performance using patient-specific adaptation by online learning.

Taming Diffusion Models for Image Restoration: A Review

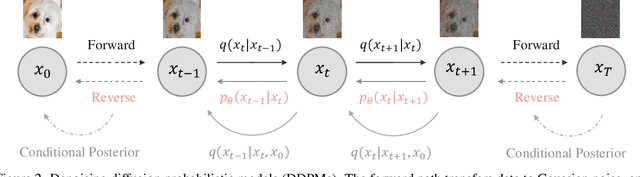
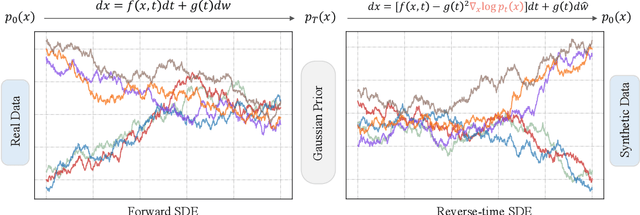
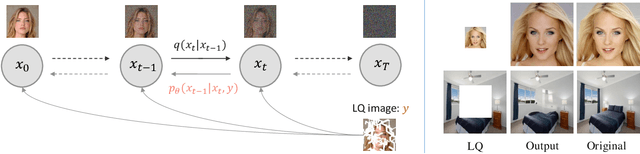
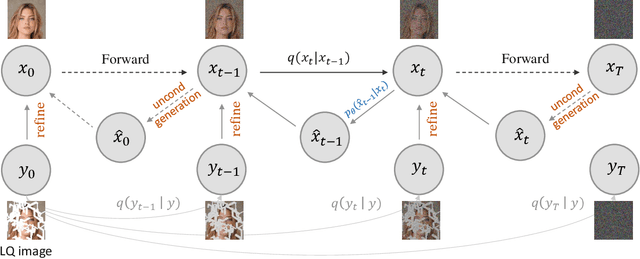
Diffusion models have achieved remarkable progress in generative modelling, particularly in enhancing image quality to conform to human preferences. Recently, these models have also been applied to low-level computer vision for photo-realistic image restoration (IR) in tasks such as image denoising, deblurring, dehazing, etc. In this review paper, we introduce key constructions in diffusion models and survey contemporary techniques that make use of diffusion models in solving general IR tasks. Furthermore, we point out the main challenges and limitations of existing diffusion-based IR frameworks and provide potential directions for future work.

Conditional sampling within generative diffusion models

Generative diffusions are a powerful class of Monte Carlo samplers that leverage bridging Markov processes to approximate complex, high-dimensional distributions, such as those found in image processing and language models. Despite their success in these domains, an important open challenge remains: extending these techniques to sample from conditional distributions, as required in, for example, Bayesian inverse problems. In this paper, we present a comprehensive review of existing computational approaches to conditional sampling within generative diffusion models. Specifically, we highlight key methodologies that either utilise the joint distribution, or rely on (pre-trained) marginal distributions with explicit likelihoods, to construct conditional generative samplers.

Learning incomplete factorization preconditioners for GMRES

In this paper, we develop a data-driven approach to generate incomplete LU factorizations of large-scale sparse matrices. The learned approximate factorization is utilized as a preconditioner for the corresponding linear equation system in the GMRES method. Incomplete factorization methods are one of the most commonly applied algebraic preconditioners for sparse linear equation systems and are able to speed up the convergence of Krylov subspace methods. However, they are sensitive to hyper-parameters and might suffer from numerical breakdown or lead to slow convergence when not properly applied. We replace the typically hand-engineered algorithms with a graph neural network based approach that is trained against data to predict an approximate factorization. This allows us to learn preconditioners tailored for a specific problem distribution. We analyze and empirically evaluate different loss functions to train the learned preconditioners and show their effectiveness to decrease the number of GMRES iterations and improve the spectral properties on our synthetic dataset. The code is available at https://github.com/paulhausner/neural-incomplete-factorization.

Conditioning diffusion models by explicit forward-backward bridging

Given an unconditional diffusion model $\pi(x, y)$, using it to perform conditional simulation $\pi(x \mid y)$ is still largely an open question and is typically achieved by learning conditional drifts to the denoising SDE after the fact. In this work, we express conditional simulation as an inference problem on an augmented space corresponding to a partial SDE bridge. This perspective allows us to implement efficient and principled particle Gibbs and pseudo-marginal samplers marginally targeting the conditional distribution $\pi(x \mid y)$. Contrary to existing methodology, our methods do not introduce any additional approximation to the unconditional diffusion model aside from the Monte Carlo error. We showcase the benefits and drawbacks of our approach on a series of synthetic and real data examples.

Efficient Radiation Treatment Planning based on Voxel Importance

Optimization is a time-consuming part of radiation treatment planning. We propose to reduce the optimization problem by only using a representative subset of informative voxels. This way, we improve planning efficiency while maintaining or enhancing the plan quality. To reduce the computational complexity of the optimization problem, we propose to subsample the set of voxels via importance sampling. We derive a sampling distribution based on an importance score that we obtain from pre-solving an easy optimization problem involving a simplified probing objective. By solving a reduced version of the original optimization problem using this subset, we effectively reduce the problem's size and computational demands while accounting for regions in which satisfactory dose deliveries are challenging. In contrast to other stochastic (sub-)sampling methods, our technique only requires a single sampling step to define a reduced optimization problem. This problem can be efficiently solved using established solvers. Empirical experiments on open benchmark data highlight substantially reduced optimization times, up to 50 times faster than the original ones, for intensity-modulated radiation therapy (IMRT), all while upholding plan quality comparable to traditional methods. Our approach has the potential to significantly accelerate radiation treatment planning by addressing its inherent computational challenges. We reduce the treatment planning time by reducing the size of the optimization problem rather than improving the optimization method. Our efforts are thus complementary to much of the previous developments.

Photo-Realistic Image Restoration in the Wild with Controlled Vision-Language Models

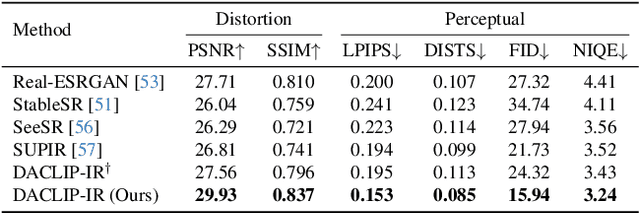
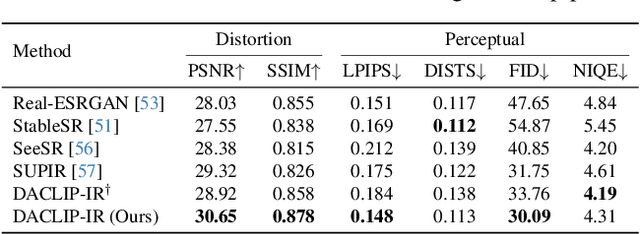
Though diffusion models have been successfully applied to various image restoration (IR) tasks, their performance is sensitive to the choice of training datasets. Typically, diffusion models trained in specific datasets fail to recover images that have out-of-distribution degradations. To address this problem, this work leverages a capable vision-language model and a synthetic degradation pipeline to learn image restoration in the wild (wild IR). More specifically, all low-quality images are simulated with a synthetic degradation pipeline that contains multiple common degradations such as blur, resize, noise, and JPEG compression. Then we introduce robust training for a degradation-aware CLIP model to extract enriched image content features to assist high-quality image restoration. Our base diffusion model is the image restoration SDE (IR-SDE). Built upon it, we further present a posterior sampling strategy for fast noise-free image generation. We evaluate our model on both synthetic and real-world degradation datasets. Moreover, experiments on the unified image restoration task illustrate that the proposed posterior sampling improves image generation quality for various degradations.

Ising on the Graph: Task-specific Graph Subsampling via the Ising Model

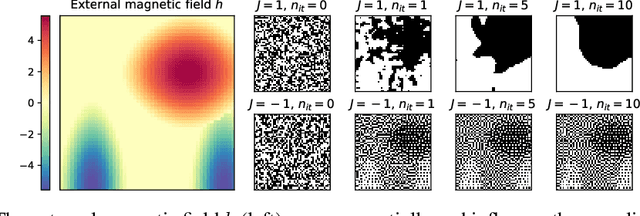
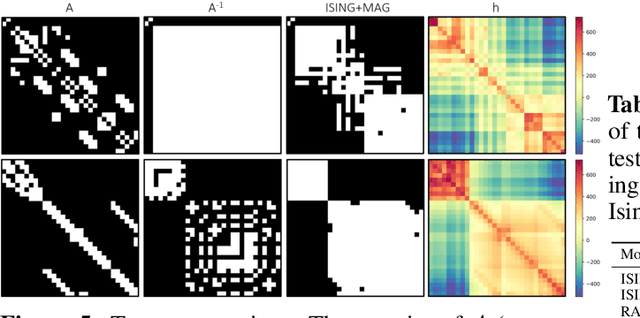
Reducing a graph while preserving its overall structure is an important problem with many applications. Typically, the reduction approaches either remove edges (sparsification) or merge nodes (coarsening) in an unsupervised way with no specific downstream task in mind. In this paper, we present an approach for subsampling graph structures using an Ising model defined on either the nodes or edges and learning the external magnetic field of the Ising model using a graph neural network. Our approach is task-specific as it can learn how to reduce a graph for a specific downstream task in an end-to-end fashion. The utilized loss function of the task does not even have to be differentiable. We showcase the versatility of our approach on three distinct applications: image segmentation, 3D shape sparsification, and sparse approximate matrix inverse determination.

Entropy-regularized Diffusion Policy with Q-Ensembles for Offline Reinforcement Learning

This paper presents advanced techniques of training diffusion policies for offline reinforcement learning (RL). At the core is a mean-reverting stochastic differential equation (SDE) that transfers a complex action distribution into a standard Gaussian and then samples actions conditioned on the environment state with a corresponding reverse-time SDE, like a typical diffusion policy. We show that such an SDE has a solution that we can use to calculate the log probability of the policy, yielding an entropy regularizer that improves the exploration of offline datasets. To mitigate the impact of inaccurate value functions from out-of-distribution data points, we further propose to learn the lower confidence bound of Q-ensembles for more robust policy improvement. By combining the entropy-regularized diffusion policy with Q-ensembles in offline RL, our method achieves state-of-the-art performance on most tasks in D4RL benchmarks. Code is available at \href{https://github.com/ruoqizzz/Entropy-Regularized-Diffusion-Policy-with-QEnsemble}{https://github.com/ruoqizzz/Entropy-Regularized-Diffusion-Policy-with-QEnsemble}.

Variational Elliptical Processes

We present elliptical processes, a family of non-parametric probabilistic models that subsume Gaussian processes and Student's t processes. This generalization includes a range of new heavy-tailed behaviors while retaining computational tractability. Elliptical processes are based on a representation of elliptical distributions as a continuous mixture of Gaussian distributions. We parameterize this mixture distribution as a spline normalizing flow, which we train using variational inference. The proposed form of the variational posterior enables a sparse variational elliptical process applicable to large-scale problems. We highlight advantages compared to Gaussian processes through regression and classification experiments. Elliptical processes can supersede Gaussian processes in several settings, including cases where the likelihood is non-Gaussian or when accurate tail modeling is essential.