Warm-starting active-set solvers using graph neural networks

Quadratic programming (QP) solvers are widely used in real-time control and optimization, but their computational cost often limits applicability in time-critical settings. We propose a learning-to-optimize approach using graph neural networks (GNNs) to predict active sets in the dual active-set solver DAQP. The method exploits the structural properties of QPs by representing them as bipartite graphs and learning to identify the optimal active set for efficiently warm-starting the solver. Across varying problem sizes, the GNN consistently reduces the number of solver iterations compared to cold-starting, while performance is comparable to a multilayer perceptron (MLP) baseline. Furthermore, a GNN trained on varying problem sizes generalizes effectively to unseen dimensions, demonstrating flexibility and scalability. These results highlight the potential of structure-aware learning to accelerate optimization in real-time applications such as model predictive control.

Learning to accelerate distributed ADMM using graph neural networks

Distributed optimization is fundamental in large-scale machine learning and control applications. Among existing methods, the Alternating Direction Method of Multipliers (ADMM) has gained popularity due to its strong convergence guarantees and suitability for decentralized computation. However, ADMM often suffers from slow convergence and sensitivity to hyperparameter choices. In this work, we show that distributed ADMM iterations can be naturally represented within the message-passing framework of graph neural networks (GNNs). Building on this connection, we propose to learn adaptive step sizes and communication weights by a graph neural network that predicts the hyperparameters based on the iterates. By unrolling ADMM for a fixed number of iterations, we train the network parameters end-to-end to minimize the final iterates error for a given problem class, while preserving the algorithm's convergence properties. Numerical experiments demonstrate that our learned variant consistently improves convergence speed and solution quality compared to standard ADMM. The code is available at https://github.com/paulhausner/learning-distributed-admm.

Learning incomplete factorization preconditioners for GMRES

In this paper, we develop a data-driven approach to generate incomplete LU factorizations of large-scale sparse matrices. The learned approximate factorization is utilized as a preconditioner for the corresponding linear equation system in the GMRES method. Incomplete factorization methods are one of the most commonly applied algebraic preconditioners for sparse linear equation systems and are able to speed up the convergence of Krylov subspace methods. However, they are sensitive to hyper-parameters and might suffer from numerical breakdown or lead to slow convergence when not properly applied. We replace the typically hand-engineered algorithms with a graph neural network based approach that is trained against data to predict an approximate factorization. This allows us to learn preconditioners tailored for a specific problem distribution. We analyze and empirically evaluate different loss functions to train the learned preconditioners and show their effectiveness to decrease the number of GMRES iterations and improve the spectral properties on our synthetic dataset. The code is available at https://github.com/paulhausner/neural-incomplete-factorization.

ICML 2023 Topological Deep Learning Challenge : Design and Results

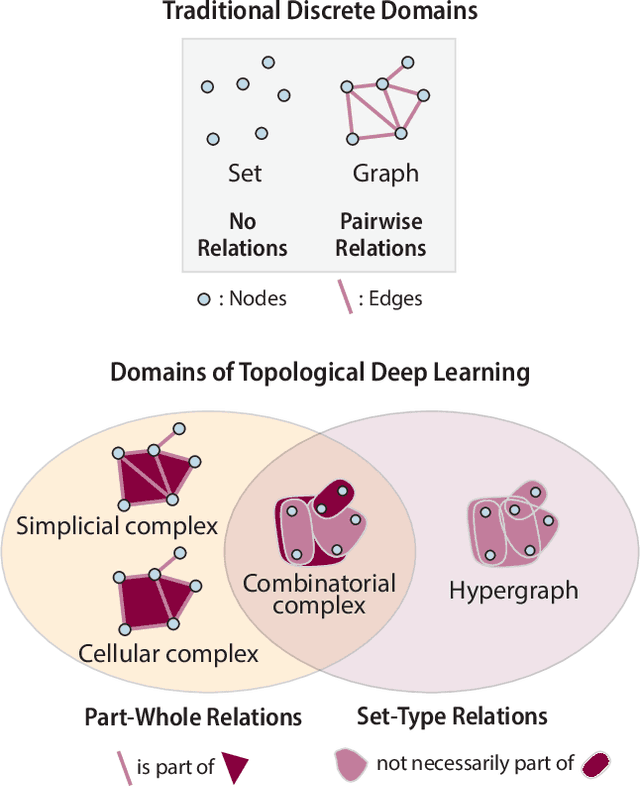
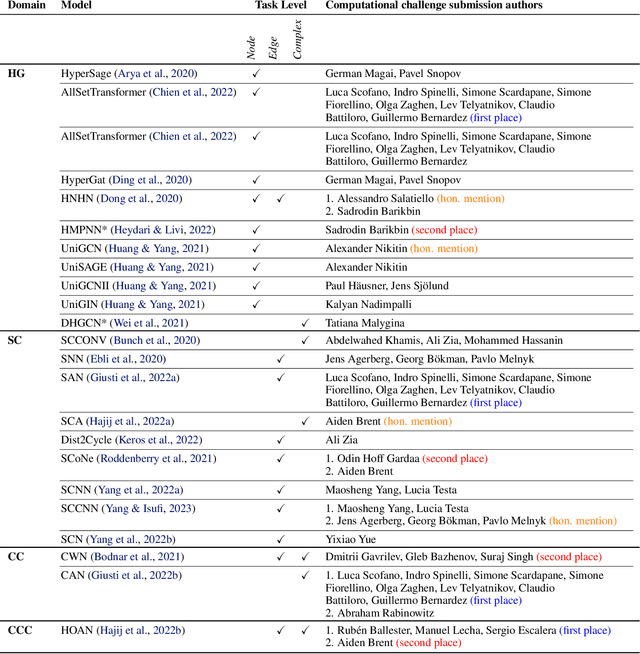
This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.

Neural incomplete factorization: learning preconditioners for the conjugate gradient method

In this paper, we develop a novel data-driven approach to accelerate solving large-scale linear equation systems encountered in scientific computing and optimization. Our method utilizes self-supervised training of a graph neural network to generate an effective preconditioner tailored to the specific problem domain. By replacing conventional hand-crafted preconditioners used with the conjugate gradient method, our approach, named neural incomplete factorization (NeuralIF), significantly speeds-up convergence and computational efficiency. At the core of our method is a novel message-passing block, inspired by sparse matrix theory, that aligns with the objective to find a sparse factorization of the matrix. We evaluate our proposed method on both a synthetic and a real-world problem arising from scientific computing. Our results demonstrate that NeuralIF consistently outperforms the most common general-purpose preconditioners, including the incomplete Cholesky method, achieving competitive performance across various metrics even outside the training data distribution.