Florian Frantzen
HLSAD: Hodge Laplacian-based Simplicial Anomaly Detection
May 30, 2025Abstract:In this paper, we propose HLSAD, a novel method for detecting anomalies in time-evolving simplicial complexes. While traditional graph anomaly detection techniques have been extensively studied, they often fail to capture changes in higher-order interactions that are crucial for identifying complex structural anomalies. These higher-order interactions can arise either directly from the underlying data itself or through graph lifting techniques. Our approach leverages the spectral properties of Hodge Laplacians of simplicial complexes to effectively model multi-way interactions among data points. By incorporating higher-dimensional simplicial structures into our method, our method enhances both detection accuracy and computational efficiency. Through comprehensive experiments on both synthetic and real-world datasets, we demonstrate that our approach outperforms existing graph methods in detecting both events and change points.
Topological Trajectory Classification and Landmark Inference on Simplicial Complexes
Dec 04, 2024Abstract:We consider the problem of classifying trajectories on a discrete or discretised 2-dimensional manifold modelled by a simplicial complex. Previous works have proposed to project the trajectories into the harmonic eigenspace of the Hodge Laplacian, and then cluster the resulting embeddings. However, if the considered space has vanishing homology (i.e., no "holes"), then the harmonic space of the 1-Hodge Laplacian is trivial and thus the approach fails. Here we propose to view this issue akin to a sensor placement problem and present an algorithm that aims to learn "optimal holes" to distinguish a set of given trajectory classes. Specifically, given a set of labelled trajectories, which we interpret as edge-flows on the underlying simplicial complex, we search for 2-simplices whose deletion results in an optimal separation of the trajectory labels according to the corresponding spectral embedding of the trajectories into the harmonic space. Finally, we generalise this approach to the unsupervised setting.
Learning From Simplicial Data Based on Random Walks and 1D Convolutions
Apr 04, 2024Abstract:Triggered by limitations of graph-based deep learning methods in terms of computational expressivity and model flexibility, recent years have seen a surge of interest in computational models that operate on higher-order topological domains such as hypergraphs and simplicial complexes. While the increased expressivity of these models can indeed lead to a better classification performance and a more faithful representation of the underlying system, the computational cost of these higher-order models can increase dramatically. To this end, we here explore a simplicial complex neural network learning architecture based on random walks and fast 1D convolutions (SCRaWl), in which we can adjust the increase in computational cost by varying the length and number of random walks considered while accounting for higher-order relationships. Importantly, due to the random walk-based design, the expressivity of the proposed architecture is provably incomparable to that of existing message-passing simplicial neural networks. We empirically evaluate SCRaWl on real-world datasets and show that it outperforms other simplicial neural networks.
TopoX: A Suite of Python Packages for Machine Learning on Topological Domains
Feb 07, 2024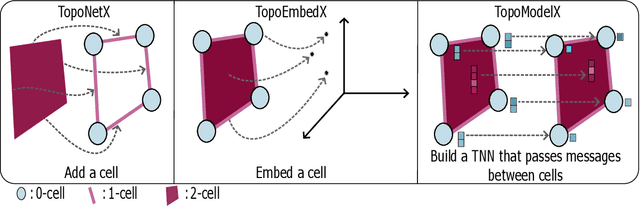
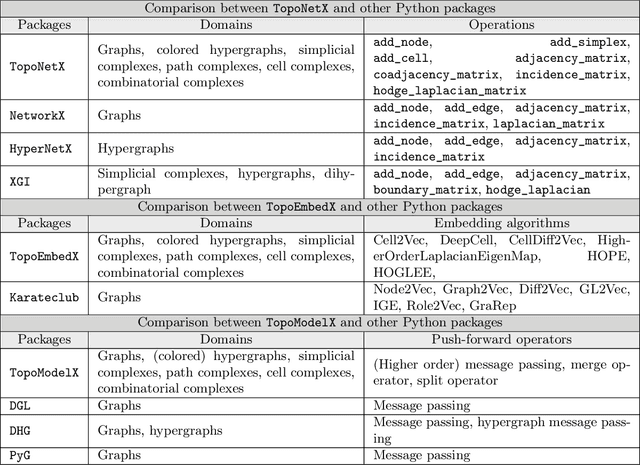
Abstract:We introduce topox, a Python software suite that provides reliable and user-friendly building blocks for computing and machine learning on topological domains that extend graphs: hypergraphs, simplicial, cellular, path and combinatorial complexes. topox consists of three packages: toponetx facilitates constructing and computing on these domains, including working with nodes, edges and higher-order cells; topoembedx provides methods to embed topological domains into vector spaces, akin to popular graph-based embedding algorithms such as node2vec; topomodelx is built on top of PyTorch and offers a comprehensive toolbox of higher-order message passing functions for neural networks on topological domains. The extensively documented and unit-tested source code of topox is available under MIT license at https://github.com/pyt-team.
ICML 2023 Topological Deep Learning Challenge : Design and Results
Oct 02, 2023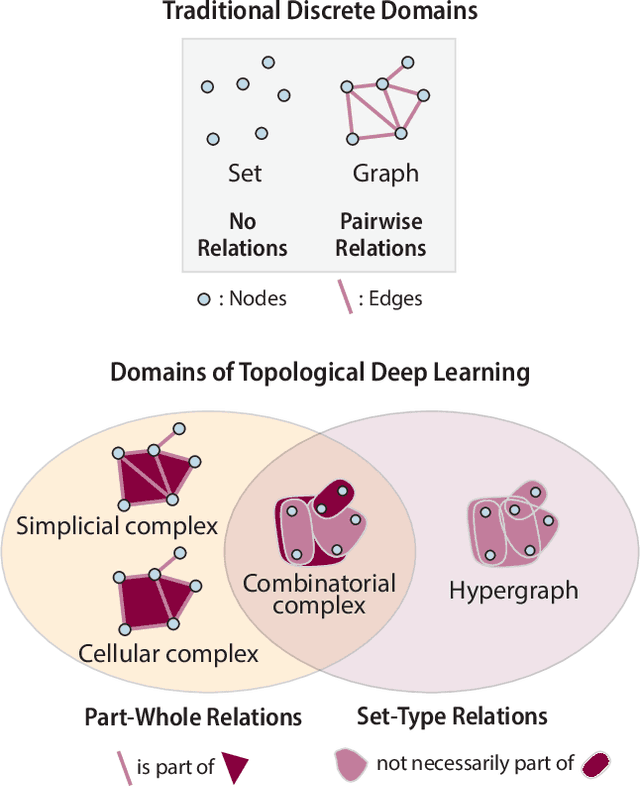
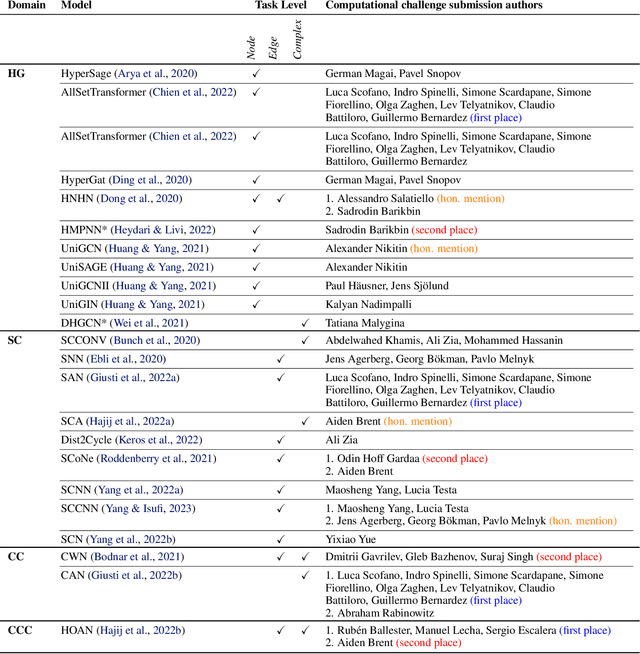
Abstract:This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.
Signal Processing on Product Spaces
Mar 18, 2023


Abstract:We establish a framework for signal processing on product spaces of simplicial and cellular complexes. For simplicity, we focus on the product of two complexes representing time and space, although our results generalize naturally to products of simplicial complexes of arbitrary dimension. Our framework leverages the structure of the eigenmodes of the Hodge Laplacian of the product space to jointly filter along time and space. To this end, we provide a decomposition theorem of the Hodge Laplacian of the product space, which highlights how the product structure induces a decomposition of each eigenmode into a spatial and temporal component. Finally, we apply our method to real world data, specifically for interpolating trajectories of buoys in the ocean from a limited set of observed trajectories.
Outlier Detection for Trajectories via Flow-embeddings
Nov 25, 2021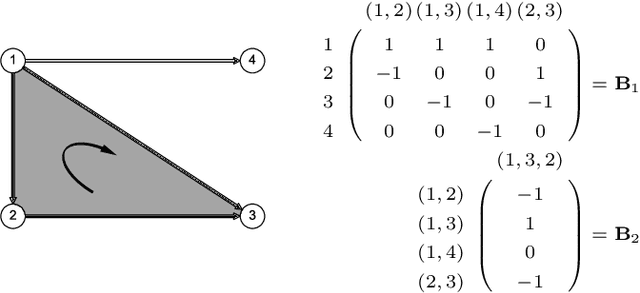
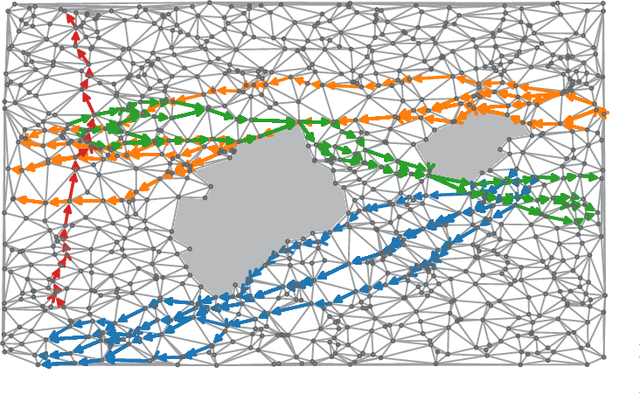
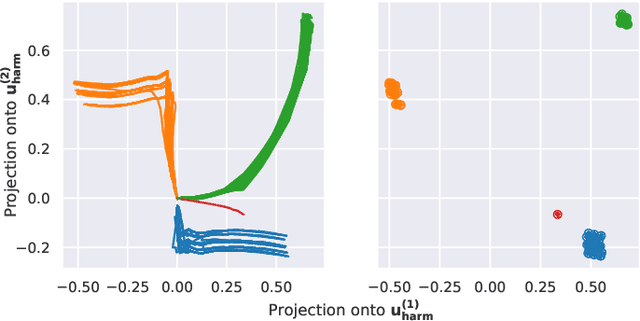
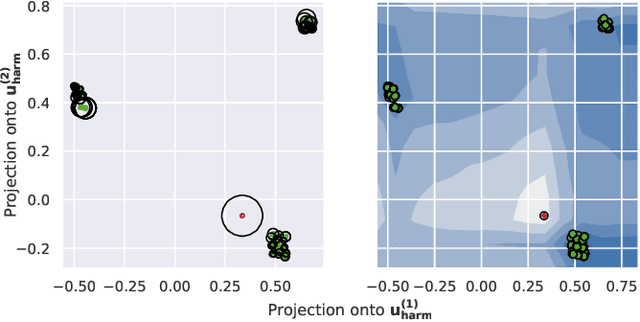
Abstract:We propose a method to detect outliers in empirically observed trajectories on a discrete or discretized manifold modeled by a simplicial complex. Our approach is similar to spectral embeddings such as diffusion-maps and Laplacian eigenmaps, that construct vertex embeddings from the eigenvectors of the graph Laplacian associated with low eigenvalues. Here we consider trajectories as edge-flow vectors defined on a simplicial complex, a higher-order generalization of graphs, and use the Hodge 1-Laplacian of the simplicial complex to derive embeddings of these edge-flows. By projecting trajectory vectors onto the eigenspace of the Hodge 1-Laplacian associated to small eigenvalues, we can characterize the behavior of the trajectories relative to the homology of the complex, which corresponds to holes in the underlying space. This enables us to classify trajectories based on simply interpretable, low-dimensional statistics. We show how this technique can single out trajectories that behave (topologically) different compared to typical trajectories, and illustrate the performance of our approach with both synthetic and empirical data.
Hodgelets: Localized Spectral Representations of Flows on Simplicial Complexes
Sep 17, 2021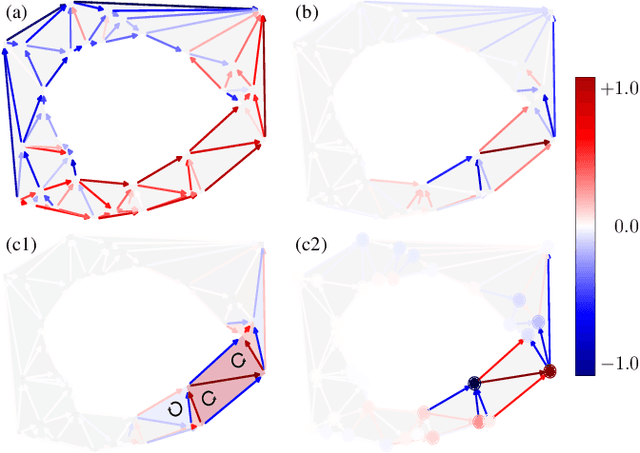
Abstract:We develop wavelet representations for edge-flows on simplicial complexes, using ideas rooted in combinatorial Hodge theory and spectral graph wavelets. We first show that the Hodge Laplacian can be used in lieu of the graph Laplacian to construct a family of wavelets for higher-order signals on simplicial complexes. Then, we refine this idea to construct wavelets that respect the Hodge-Helmholtz decomposition. For these Hodgelets, familiar notions of curl-free and divergence-free flows from vector calculus are preserved. We characterize the representational quality of our Hodgelets for edge flows in terms of frame bounds and demonstrate the use of these spectral wavelets for sparse representation of edge flows on real and synthetic data.
Signal processing on simplicial complexes
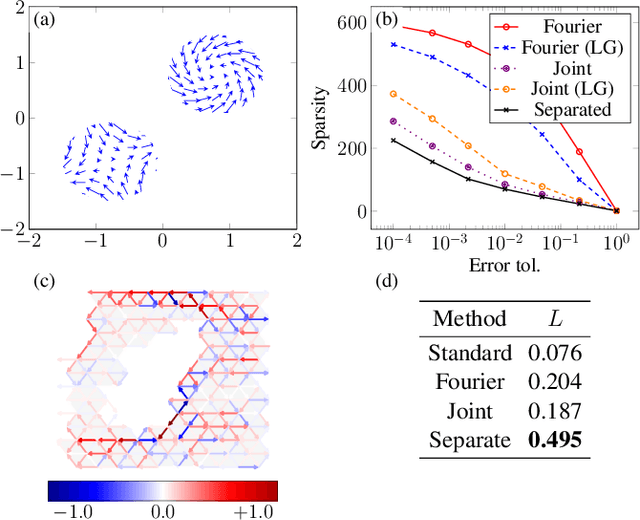
Jun 14, 2021
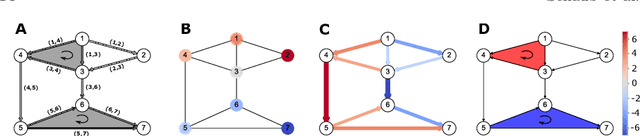
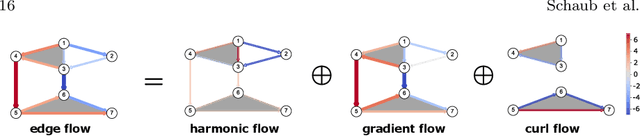
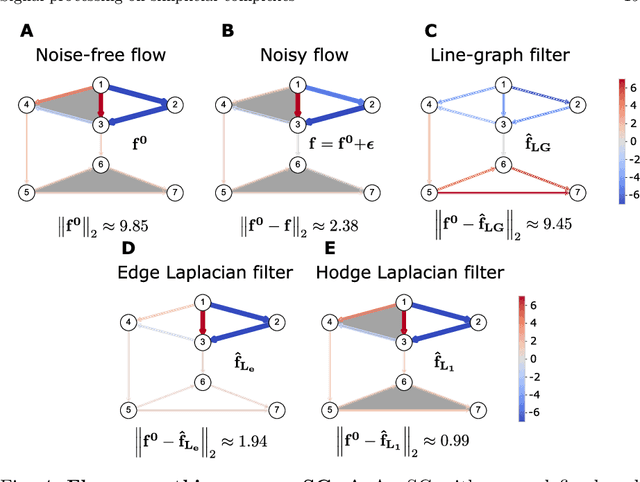
Abstract:Higher-order networks have so far been considered primarily in the context of studying the structure of complex systems, i.e., the higher-order or multi-way relations connecting the constituent entities. More recently, a number of studies have considered dynamical processes that explicitly account for such higher-order dependencies, e.g., in the context of epidemic spreading processes or opinion formation. In this chapter, we focus on a closely related, but distinct third perspective: how can we use higher-order relationships to process signals and data supported on higher-order network structures. In particular, we survey how ideas from signal processing of data supported on regular domains, such as time series or images, can be extended to graphs and simplicial complexes. We discuss Fourier analysis, signal denoising, signal interpolation, and nonlinear processing through neural networks based on simplicial complexes. Key to our developments is the Hodge Laplacian matrix, a multi-relational operator that leverages the special structure of simplicial complexes and generalizes desirable properties of the Laplacian matrix in graph signal processing.
The Effects of Randomness on the Stability of Node Embeddings
May 20, 2020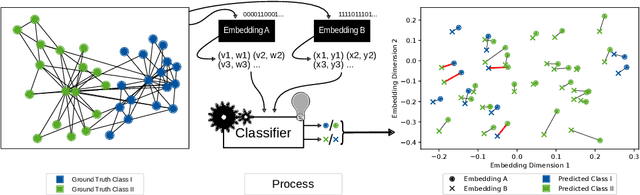
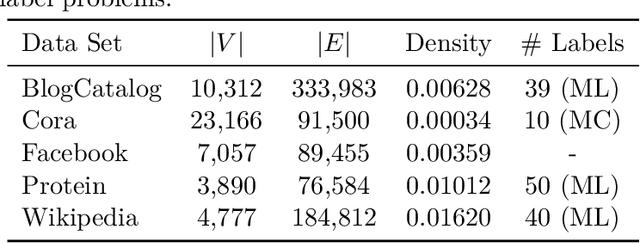
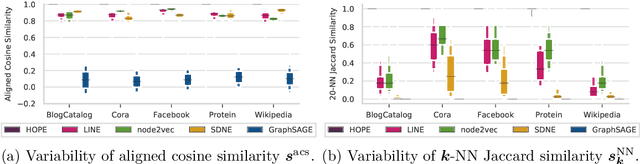
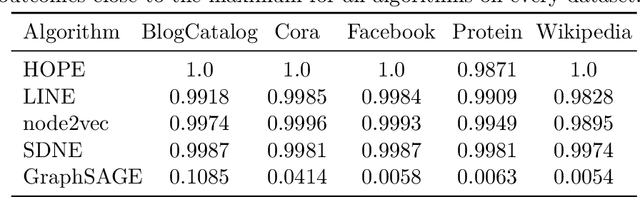
Abstract:We systematically evaluate the (in-)stability of state-of-the-art node embedding algorithms due to randomness, i.e., the random variation of their outcomes given identical algorithms and graphs. We apply five node embeddings algorithms---HOPE, LINE, node2vec, SDNE, and GraphSAGE---to synthetic and empirical graphs and assess their stability under randomness with respect to (i) the geometry of embedding spaces as well as (ii) their performance in downstream tasks. We find significant instabilities in the geometry of embedding spaces independent of the centrality of a node. In the evaluation of downstream tasks, we find that the accuracy of node classification seems to be unaffected by random seeding while the actual classification of nodes can vary significantly. This suggests that instability effects need to be taken into account when working with node embeddings. Our work is relevant for researchers and engineers interested in the effectiveness, reliability, and reproducibility of node embedding approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge