Parallelised Differentiable Straightest Geodesics for 3D Meshes

Machine learning has been progressively generalised to operate within non-Euclidean domains, but geometrically accurate methods for learning on surfaces are still falling behind. The lack of closed-form Riemannian operators, the non-differentiability of their discrete counterparts, and poor parallelisation capabilities have been the main obstacles to the development of the field on meshes. A principled framework to compute the exponential map on Riemannian surfaces discretised as meshes is straightest geodesics, which also allows to trace geodesics and parallel-transport vectors as a by-product. We provide a parallel GPU implementation and derive two different methods for differentiating through the straightest geodesics, one leveraging an extrinsic proxy function and one based upon a geodesic finite differences scheme. After proving our parallelisation performance and accuracy, we demonstrate how our differentiable exponential map can improve learning and optimisation pipelines on general geometries. In particular, to showcase the versatility of our method, we propose a new geodesic convolutional layer, a new flow matching method for learning on meshes, and a second-order optimiser that we apply to centroidal Voronoi tessellation. Our code, models, and pip-installable library (digeo) are available at: circle-group.github.io/research/DSG.

From Data Statistics to Feature Geometry: How Correlations Shape Superposition

A central idea in mechanistic interpretability is that neural networks represent more features than they have dimensions, arranging them in superposition to form an over-complete basis. This framing has been influential, motivating dictionary learning approaches such as sparse autoencoders. However, superposition has mostly been studied in idealized settings where features are sparse and uncorrelated. In these settings, superposition is typically understood as introducing interference that must be minimized geometrically and filtered out by non-linearities such as ReLUs, yielding local structures like regular polytopes. We show that this account is incomplete for realistic data by introducing Bag-of-Words Superposition (BOWS), a controlled setting to encode binary bag-of-words representations of internet text in superposition. Using BOWS, we find that when features are correlated, interference can be constructive rather than just noise to be filtered out. This is achieved by arranging features according to their co-activation patterns, making interference between active features constructive, while still using ReLUs to avoid false positives. We show that this kind of arrangement is more prevalent in models trained with weight decay and naturally gives rise to semantic clusters and cyclical structures which have been observed in real language models yet were not explained by the standard picture of superposition. Code for this paper can be found at https://github.com/LucasPrietoAl/correlations-feature-geometry.

TopoOR: A Unified Topological Scene Representation for the Operating Room

Surgical Scene Graphs abstract the complexity of surgical operating rooms (OR) into a structure of entities and their relations, but existing paradigms suffer from strictly dyadic structural limitations. Frameworks that predominantly rely on pairwise message passing or tokenized sequences flatten the manifold geometry inherent to relational structures and lose structure in the process. We introduce TopoOR, a new paradigm that models multimodal operating rooms as a higher-order structure, innately preserving pairwise and group relationships. By lifting interactions between entities into higher-order topological cells, TopoOR natively models complex dynamics and multimodality present in the OR. This topological representation subsumes traditional scene graphs, thereby offering strictly greater expressivity. We also propose a higher-order attention mechanism that explicitly preserves manifold structure and modality-specific features throughout hierarchical relational attention. In this way, we circumvent combining 3D geometry, audio, and robot kinematics into a single joint latent representation, preserving the precise multimodal structure required for safety-critical reasoning, unlike existing methods. Extensive experiments demonstrate that our approach outperforms traditional graph and LLM-based baselines across sterility breach detection, robot phase prediction, and next-action anticipation

COMPOSE: Hypergraph Cover Optimization for Multi-view 3D Human Pose Estimation

3D pose estimation from sparse multi-views is a critical task for numerous applications, including action recognition, sports analysis, and human-robot interaction. Optimization-based methods typically follow a two-stage pipeline, first detecting 2D keypoints in each view and then associating these detections across views to triangulate the 3D pose. Existing methods rely on mere pairwise associations to model this correspondence problem, treating global consistency between views (i.e., cycle consistency) as a soft constraint. Yet, reconciling these constraints for multiple views becomes brittle when spurious associations propagate errors. We thus propose COMPOSE, a novel framework that formulates multi-view pose correspondence matching as a hypergraph partitioning problem rather than through pairwise association. While the complexity of the resulting integer linear program grows exponentially in theory, we introduce an efficient geometric pruning strategy to substantially reduce the search space. COMPOSE achieves improvements of up to 23% in average precision over previous optimization-based methods and up to 11% over self-supervised end-to-end learned methods, offering a promising solution to a widely studied problem.

MoLingo: Motion-Language Alignment for Text-to-Motion Generation

We introduce MoLingo, a text-to-motion (T2M) model that generates realistic, lifelike human motion by denoising in a continuous latent space. Recent works perform latent space diffusion, either on the whole latent at once or auto-regressively over multiple latents. In this paper, we study how to make diffusion on continuous motion latents work best. We focus on two questions: (1) how to build a semantically aligned latent space so diffusion becomes more effective, and (2) how to best inject text conditioning so the motion follows the description closely. We propose a semantic-aligned motion encoder trained with frame-level text labels so that latents with similar text meaning stay close, which makes the latent space more diffusion-friendly. We also compare single-token conditioning with a multi-token cross-attention scheme and find that cross-attention gives better motion realism and text-motion alignment. With semantically aligned latents, auto-regressive generation, and cross-attention text conditioning, our model sets a new state of the art in human motion generation on standard metrics and in a user study. We will release our code and models for further research and downstream usage.

CuMPerLay: Learning Cubical Multiparameter Persistence Vectorizations

We present CuMPerLay, a novel differentiable vectorization layer that enables the integration of Cubical Multiparameter Persistence (CMP) into deep learning pipelines. While CMP presents a natural and powerful way to topologically work with images, its use is hindered by the complexity of multifiltration structures as well as the vectorization of CMP. In face of these challenges, we introduce a new algorithm for vectorizing MP homologies of cubical complexes. Our CuMPerLay decomposes the CMP into a combination of individual, learnable single-parameter persistence, where the bifiltration functions are jointly learned. Thanks to the differentiability, its robust topological feature vectors can be seamlessly used within state-of-the-art architectures such as Swin Transformers. We establish theoretical guarantees for the stability of our vectorization under generalized Wasserstein metrics. Our experiments on benchmark medical imaging and computer vision datasets show the benefit CuMPerLay on classification and segmentation performance, particularly in limited-data scenarios. Overall, CuMPerLay offers a promising direction for integrating global structural information into deep networks for structured image analysis.

Quantum-enhanced Computer Vision: Going Beyond Classical Algorithms

Quantum-enhanced Computer Vision (QeCV) is a new research field at the intersection of computer vision, optimisation theory, machine learning and quantum computing. It has high potential to transform how visual signals are processed and interpreted with the help of quantum computing that leverages quantum-mechanical effects in computations inaccessible to classical (i.e. non-quantum) computers. In scenarios where existing non-quantum methods cannot find a solution in a reasonable time or compute only approximate solutions, quantum computers can provide, among others, advantages in terms of better time scalability for multiple problem classes. Parametrised quantum circuits can also become, in the long term, a considerable alternative to classical neural networks in computer vision. However, specialised and fundamentally new algorithms must be developed to enable compatibility with quantum hardware and unveil the potential of quantum computational paradigms in computer vision. This survey contributes to the existing literature on QeCV with a holistic review of this research field. It is designed as a quantum computing reference for the computer vision community, targeting computer vision students, scientists and readers with related backgrounds who want to familiarise themselves with QeCV. We provide a comprehensive introduction to QeCV, its specifics, and methodologies for formulations compatible with quantum hardware and QeCV methods, leveraging two main quantum computational paradigms, i.e. gate-based quantum computing and quantum annealing. We elaborate on the operational principles of quantum computers and the available tools to access, program and simulate them in the context of QeCV. Finally, we review existing quantum computing tools and learning materials and discuss aspects related to publishing and reviewing QeCV papers, open challenges and potential social implications.

Geometric Neural Distance Fields for Learning Human Motion Priors

We introduce Neural Riemannian Motion Fields (NRMF), a novel 3D generative human motion prior that enables robust, temporally consistent, and physically plausible 3D motion recovery. Unlike existing VAE or diffusion-based methods, our higher-order motion prior explicitly models the human motion in the zero level set of a collection of neural distance fields (NDFs) corresponding to pose, transition (velocity), and acceleration dynamics. Our framework is rigorous in the sense that our NDFs are constructed on the product space of joint rotations, their angular velocities, and angular accelerations, respecting the geometry of the underlying articulations. We further introduce: (i) a novel adaptive-step hybrid algorithm for projecting onto the set of plausible motions, and (ii) a novel geometric integrator to "roll out" realistic motion trajectories during test-time-optimization and generation. Our experiments show significant and consistent gains: trained on the AMASS dataset, NRMF remarkably generalizes across multiple input modalities and to diverse tasks ranging from denoising to motion in-betweening and fitting to partial 2D / 3D observations.

Forecasting Continuous Non-Conservative Dynamical Systems in SO(3)

Modeling the rotation of moving objects is a fundamental task in computer vision, yet $SO(3)$ extrapolation still presents numerous challenges: (1) unknown quantities such as the moment of inertia complicate dynamics, (2) the presence of external forces and torques can lead to non-conservative kinematics, and (3) estimating evolving state trajectories under sparse, noisy observations requires robustness. We propose modeling trajectories of noisy pose estimates on the manifold of 3D rotations in a physically and geometrically meaningful way by leveraging Neural Controlled Differential Equations guided with $SO(3)$ Savitzky-Golay paths. Existing extrapolation methods often rely on energy conservation or constant velocity assumptions, limiting their applicability in real-world scenarios involving non-conservative forces. In contrast, our approach is agnostic to energy and momentum conservation while being robust to input noise, making it applicable to complex, non-inertial systems. Our approach is easily integrated as a module in existing pipelines and generalizes well to trajectories with unknown physical parameters. By learning to approximate object dynamics from noisy states during training, our model attains robust extrapolation capabilities in simulation and various real-world settings. Code is available at https://github.com/bastianlb/forecasting-rotational-dynamics

Large Learning Rates Simultaneously Achieve Robustness to Spurious Correlations and Compressibility

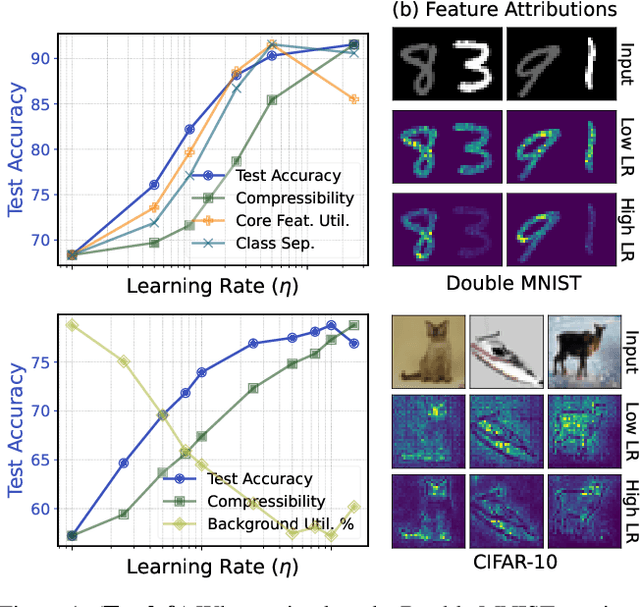
Robustness and resource-efficiency are two highly desirable properties for modern machine learning models. However, achieving them jointly remains a challenge. In this paper, we position high learning rates as a facilitator for simultaneously achieving robustness to spurious correlations and network compressibility. We demonstrate that large learning rates also produce desirable representation properties such as invariant feature utilization, class separation, and activation sparsity. Importantly, our findings indicate that large learning rates compare favorably to other hyperparameters and regularization methods, in consistently satisfying these properties in tandem. In addition to demonstrating the positive effect of large learning rates across diverse spurious correlation datasets, models, and optimizers, we also present strong evidence that the previously documented success of large learning rates in standard classification tasks is likely due to its effect on addressing hidden/rare spurious correlations in the training dataset.