Nathan Mankovich
A Flag Decomposition for Hierarchical Datasets
Feb 11, 2025Abstract:Flag manifolds encode hierarchical nested sequences of subspaces and serve as powerful structures for various computer vision and machine learning applications. Despite their utility in tasks such as dimensionality reduction, motion averaging, and subspace clustering, current applications are often restricted to extracting flags using common matrix decomposition methods like the singular value decomposition. Here, we address the need for a general algorithm to factorize and work with hierarchical datasets. In particular, we propose a novel, flag-based method that decomposes arbitrary hierarchical real-valued data into a hierarchy-preserving flag representation in Stiefel coordinates. Our work harnesses the potential of flag manifolds in applications including denoising, clustering, and few-shot learning.
Recovering Latent Confounders from High-dimensional Proxy Variables
Mar 21, 2024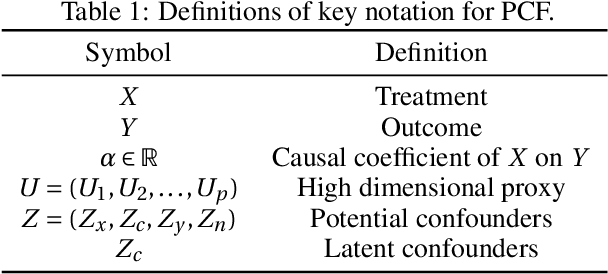
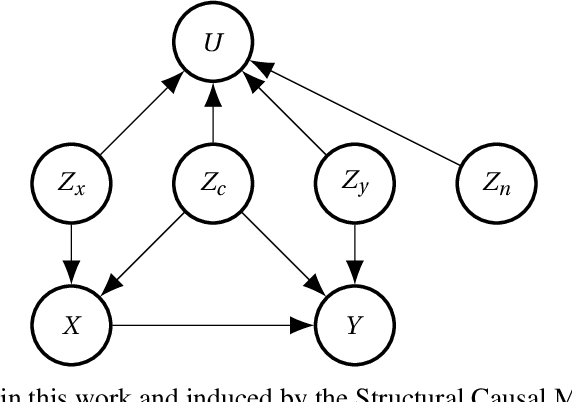
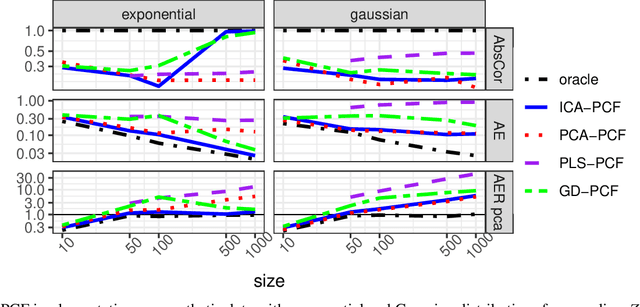

Abstract:Detecting latent confounders from proxy variables is an essential problem in causal effect estimation. Previous approaches are limited to low-dimensional proxies, sorted proxies, and binary treatments. We remove these assumptions and present a novel Proxy Confounder Factorization (PCF) framework for continuous treatment effect estimation when latent confounders manifest through high-dimensional, mixed proxy variables. For specific sample sizes, our two-step PCF implementation, using Independent Component Analysis (ICA-PCF), and the end-to-end implementation, using Gradient Descent (GD-PCF), achieve high correlation with the latent confounder and low absolute error in causal effect estimation with synthetic datasets in the high sample size regime. Even when faced with climate data, ICA-PCF recovers four components that explain $75.9\%$ of the variance in the North Atlantic Oscillation, a known confounder of precipitation patterns in Europe. Code for our PCF implementations and experiments can be found here: https://github.com/IPL-UV/confound_it. The proposed methodology constitutes a stepping stone towards discovering latent confounders and can be applied to many problems in disciplines dealing with high-dimensional observed proxies, e.g., spatiotemporal fields.
Improving generalisation via anchor multivariate analysis
Mar 11, 2024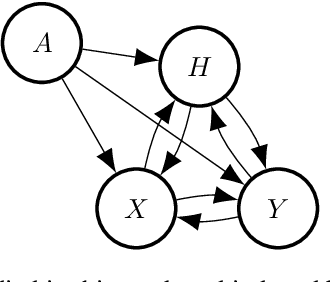



Abstract:We introduce a causal regularisation extension to anchor regression (AR) for improved out-of-distribution (OOD) generalisation. We present anchor-compatible losses, aligning with the anchor framework to ensure robustness against distribution shifts. Various multivariate analysis (MVA) algorithms, such as (Orthonormalized) PLS, RRR, and MLR, fall within the anchor framework. We observe that simple regularisation enhances robustness in OOD settings. Estimators for selected algorithms are provided, showcasing consistency and efficacy in synthetic and real-world climate science problems. The empirical validation highlights the versatility of anchor regularisation, emphasizing its compatibility with MVA approaches and its role in enhancing replicability while guarding against distribution shifts. The extended AR framework advances causal inference methodologies, addressing the need for reliable OOD generalisation.
Fun with Flags: Robust Principal Directions via Flag Manifolds
Jan 08, 2024Abstract:Principal component analysis (PCA), along with its extensions to manifolds and outlier contaminated data, have been indispensable in computer vision and machine learning. In this work, we present a unifying formalism for PCA and its variants, and introduce a framework based on the flags of linear subspaces, \ie a hierarchy of nested linear subspaces of increasing dimension, which not only allows for a common implementation but also yields novel variants, not explored previously. We begin by generalizing traditional PCA methods that either maximize variance or minimize reconstruction error. We expand these interpretations to develop a wide array of new dimensionality reduction algorithms by accounting for outliers and the data manifold. To devise a common computational approach, we recast robust and dual forms of PCA as optimization problems on flag manifolds. We then integrate tangent space approximations of principal geodesic analysis (tangent-PCA) into this flag-based framework, creating novel robust and dual geodesic PCA variations. The remarkable flexibility offered by the 'flagification' introduced here enables even more algorithmic variants identified by specific flag types. Last but not least, we propose an effective convergent solver for these flag-formulations employing the Stiefel manifold. Our empirical results on both real-world and synthetic scenarios, demonstrate the superiority of our novel algorithms, especially in terms of robustness to outliers on manifolds.
Featurizing Koopman Mode Decomposition
Dec 20, 2023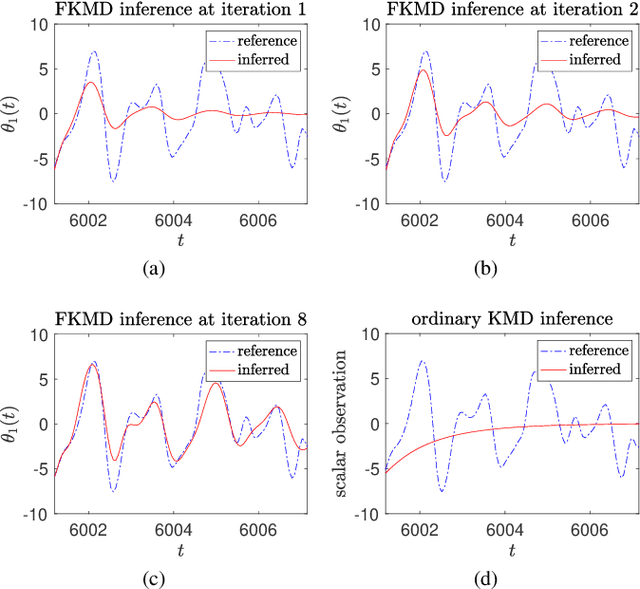
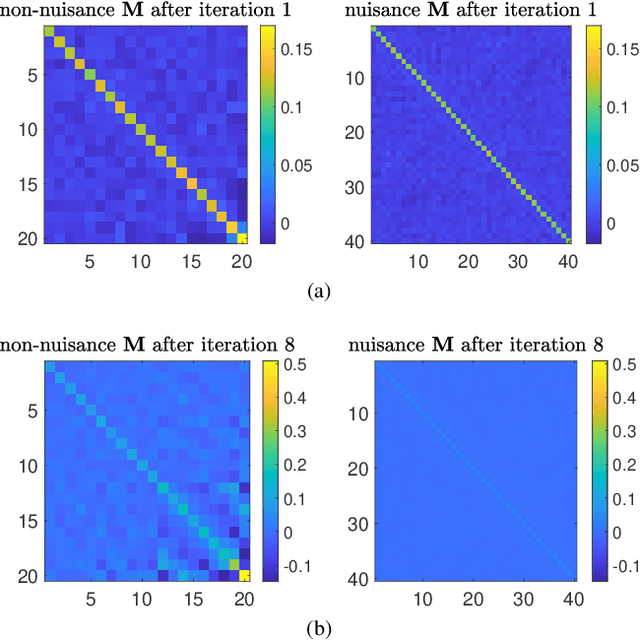
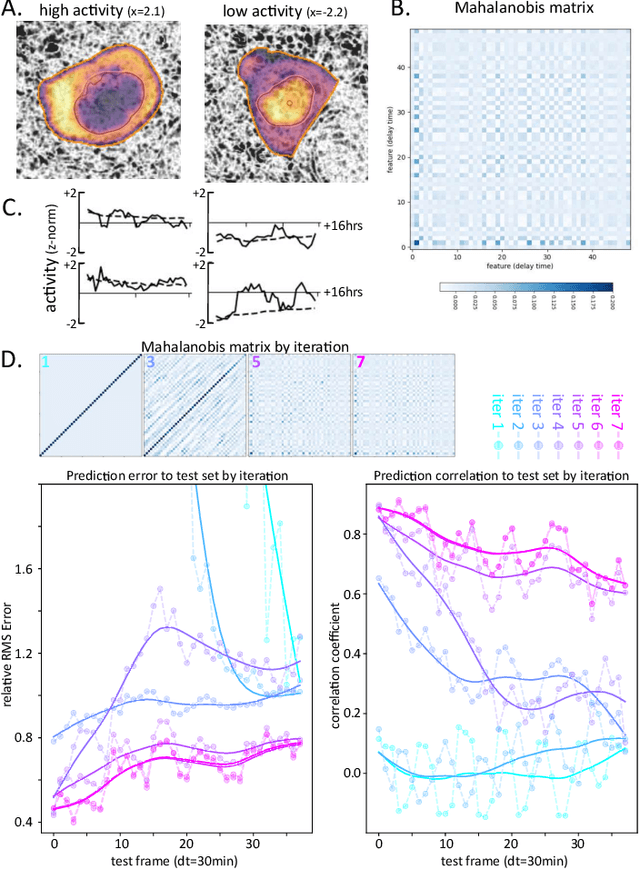

Abstract:This article introduces an advanced Koopman mode decomposition (KMD) technique -- coined Featurized Koopman Mode Decomposition (FKMD) -- that uses time embedding and Mahalanobis scaling to enhance analysis and prediction of high dimensional dynamical systems. The time embedding expands the observation space to better capture underlying manifold structure, while the Mahalanobis scaling, applied to kernel or random Fourier features, adjusts observations based on the system's dynamics. This aids in featurizing KMD in cases where good features are not a priori known. We show that our method improves KMD predictions for a high dimensional Lorenz attractor and for a cell signaling problem from cancer research.
Chordal Averaging on Flag Manifolds and Its Applications
Mar 23, 2023Abstract:This paper presents a new, provably-convergent algorithm for computing the flag-mean and flag-median of a set of points on a flag manifold under the chordal metric. The flag manifold is a mathematical space consisting of flags, which are sequences of nested subspaces of a vector space that increase in dimension. The flag manifold is a superset of a wide range of known matrix groups, including Stiefel and Grassmanians, making it a general object that is useful in a wide variety computer vision problems. To tackle the challenge of computing first order flag statistics, we first transform the problem into one that involves auxiliary variables constrained to the Stiefel manifold. The Stiefel manifold is a space of orthogonal frames, and leveraging the numerical stability and efficiency of Stiefel-manifold optimization enables us to compute the flag-mean effectively. Through a series of experiments, we show the competence of our method in Grassmann and rotation averaging, as well as principal component analysis.
The Flag Median and FlagIRLS
Mar 08, 2022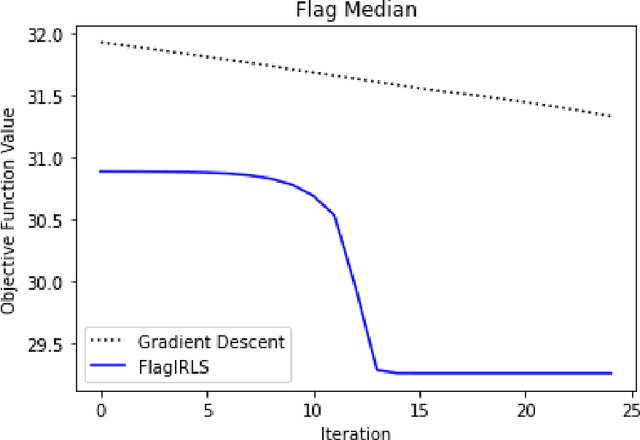
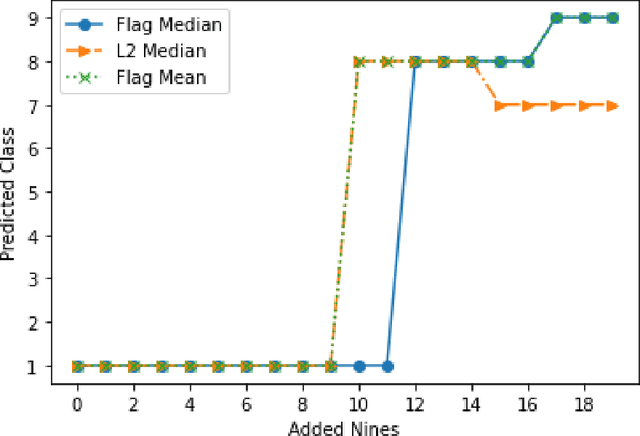
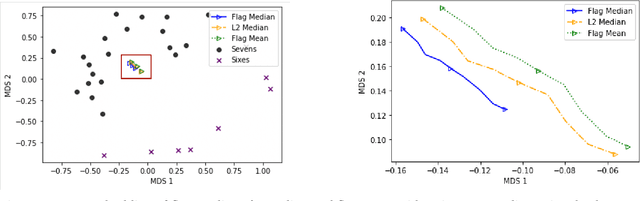
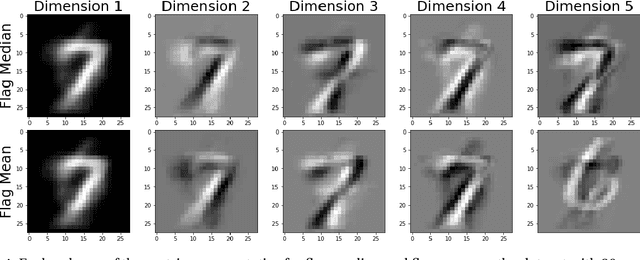
Abstract:Finding prototypes (e.g., mean and median) for a dataset is central to a number of common machine learning algorithms. Subspaces have been shown to provide useful, robust representations for datasets of images, videos and more. Since subspaces correspond to points on a Grassmann manifold, one is led to consider the idea of a subspace prototype for a Grassmann-valued dataset. While a number of different subspace prototypes have been described, the calculation of some of these prototypes has proven to be computationally expensive while other prototypes are affected by outliers and produce highly imperfect clustering on noisy data. This work proposes a new subspace prototype, the flag median, and introduces the FlagIRLS algorithm for its calculation. We provide evidence that the flag median is robust to outliers and can be used effectively in algorithms like Linde-Buzo-Grey (LBG) to produce improved clusterings on Grassmannians. Numerical experiments include a synthetic dataset, the MNIST handwritten digits dataset, the Mind's Eye video dataset and the UCF YouTube action dataset. The flag median is compared the other leading algorithms for computing prototypes on the Grassmannian, namely, the $\ell_2$-median and to the flag mean. We find that using FlagIRLS to compute the flag median converges in $4$ iterations on a synthetic dataset. We also see that Grassmannian LBG with a codebook size of $20$ and using the flag median produces at least a $10\%$ improvement in cluster purity over Grassmannian LBG using the flag mean or $\ell_2$-median on the Mind's Eye dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge