Recovering Latent Confounders from High-dimensional Proxy Variables

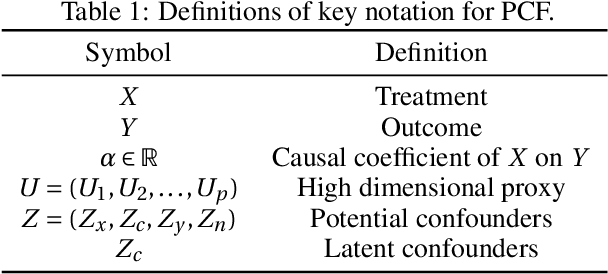
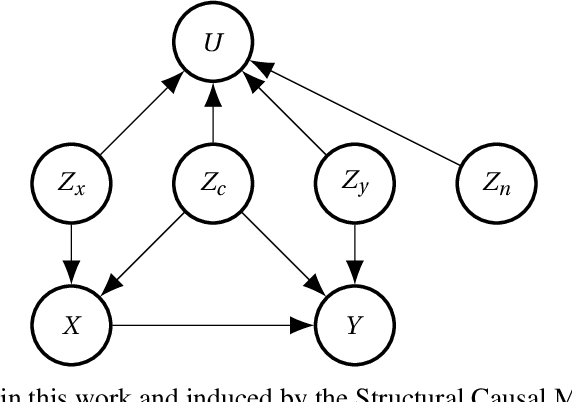
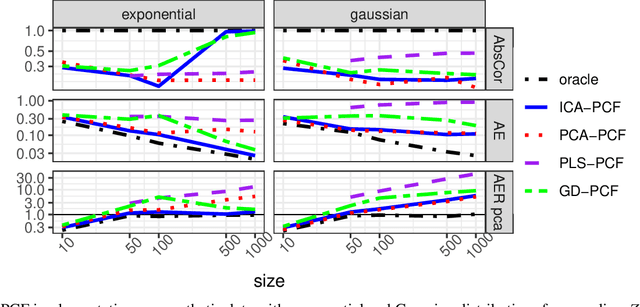
Detecting latent confounders from proxy variables is an essential problem in causal effect estimation. Previous approaches are limited to low-dimensional proxies, sorted proxies, and binary treatments. We remove these assumptions and present a novel Proxy Confounder Factorization (PCF) framework for continuous treatment effect estimation when latent confounders manifest through high-dimensional, mixed proxy variables. For specific sample sizes, our two-step PCF implementation, using Independent Component Analysis (ICA-PCF), and the end-to-end implementation, using Gradient Descent (GD-PCF), achieve high correlation with the latent confounder and low absolute error in causal effect estimation with synthetic datasets in the high sample size regime. Even when faced with climate data, ICA-PCF recovers four components that explain $75.9\%$ of the variance in the North Atlantic Oscillation, a known confounder of precipitation patterns in Europe. Code for our PCF implementations and experiments can be found here: https://github.com/IPL-UV/confound_it. The proposed methodology constitutes a stepping stone towards discovering latent confounders and can be applied to many problems in disciplines dealing with high-dimensional observed proxies, e.g., spatiotemporal fields.

Improving generalisation via anchor multivariate analysis

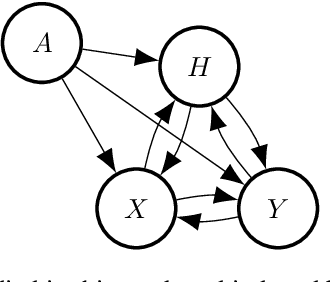
We introduce a causal regularisation extension to anchor regression (AR) for improved out-of-distribution (OOD) generalisation. We present anchor-compatible losses, aligning with the anchor framework to ensure robustness against distribution shifts. Various multivariate analysis (MVA) algorithms, such as (Orthonormalized) PLS, RRR, and MLR, fall within the anchor framework. We observe that simple regularisation enhances robustness in OOD settings. Estimators for selected algorithms are provided, showcasing consistency and efficacy in synthetic and real-world climate science problems. The empirical validation highlights the versatility of anchor regularisation, emphasizing its compatibility with MVA approaches and its role in enhancing replicability while guarding against distribution shifts. The extended AR framework advances causal inference methodologies, addressing the need for reliable OOD generalisation.

Semi-automatic tuning of coupled climate models with multiple intrinsic timescales: lessons learned from the Lorenz96 model

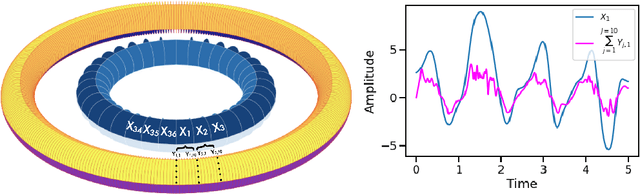
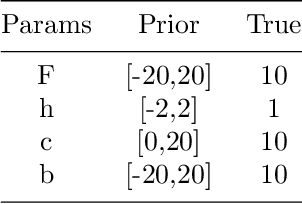
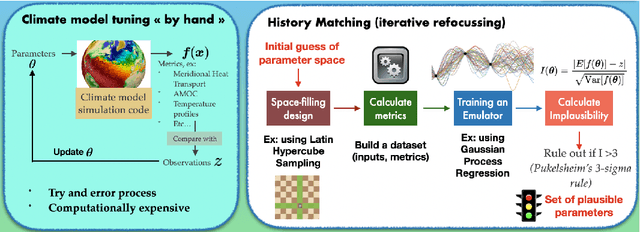
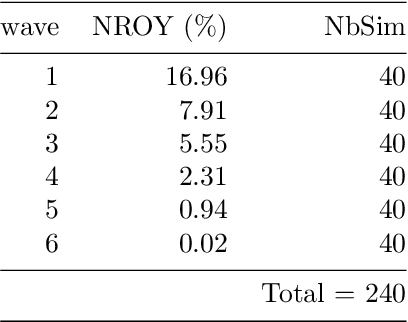
The objective of this study is to evaluate the potential for History Matching (HM) to tune a climate system with multi-scale dynamics. By considering a toy climate model, namely, the two-scale Lorenz96 model and producing experiments in perfect-model setting, we explore in detail how several built-in choices need to be carefully tested. We also demonstrate the importance of introducing physical expertise in the range of parameters, a priori to running HM. Finally we revisit a classical procedure in climate model tuning, that consists of tuning the slow and fast components separately. By doing so in the Lorenz96 model, we illustrate the non-uniqueness of plausible parameters and highlight the specificity of metrics emerging from the coupling. This paper contributes also to bridging the communities of uncertainty quantification, machine learning and climate modeling, by making connections between the terms used by each community for the same concept and presenting promising collaboration avenues that would benefit climate modeling research.