Semi-automatic tuning of coupled climate models with multiple intrinsic timescales: lessons learned from the Lorenz96 model

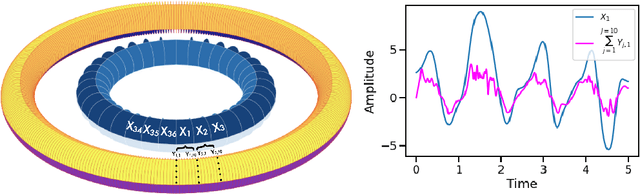
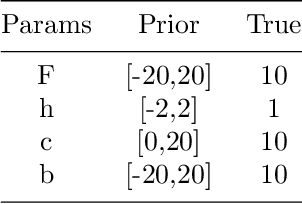
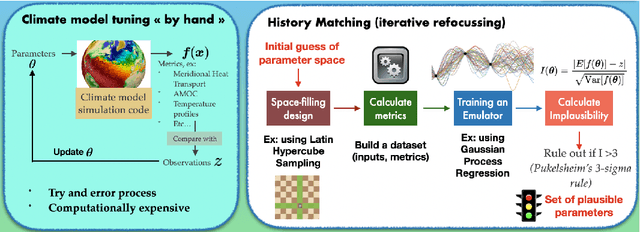
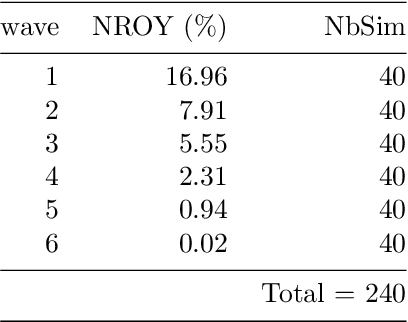
The objective of this study is to evaluate the potential for History Matching (HM) to tune a climate system with multi-scale dynamics. By considering a toy climate model, namely, the two-scale Lorenz96 model and producing experiments in perfect-model setting, we explore in detail how several built-in choices need to be carefully tested. We also demonstrate the importance of introducing physical expertise in the range of parameters, a priori to running HM. Finally we revisit a classical procedure in climate model tuning, that consists of tuning the slow and fast components separately. By doing so in the Lorenz96 model, we illustrate the non-uniqueness of plausible parameters and highlight the specificity of metrics emerging from the coupling. This paper contributes also to bridging the communities of uncertainty quantification, machine learning and climate modeling, by making connections between the terms used by each community for the same concept and presenting promising collaboration avenues that would benefit climate modeling research.

Climbing down Charney's ladder: Machine Learning and the post-Dennard era of computational climate science

The advent of digital computing in the 1950s sparked a revolution in the science of weather and climate. Meteorology, long practised as an art based on extrapolating patterns in space and time, gave way to computational methods in a decade of advances in numerical weather forecasting. Those same methods also gave rise to computational climate science, studying the behaviour of those same numerical equations over very long time intervals, and changes in external boundary conditions. Several subsequent decades of exponential growth in computational power have brought us to the present day, where models ever grow in resolution and complexity, capable of mastery of many small-scale phenomena with global repercussions, and ever more intricate feedbacks in the Earth system. We have also come to understand the central role played by randomness in an underdetermined physical system. The current juncture in computing, seven decades later, heralds an end to ever smaller computational units and ever faster arithmetic, what is called Dennard scaling. This is prompting a fundamental change in our approach to the simulation of weather and climate, potentially as revolutionary as that wrought by John von Neumann in the 1950s. One approach could return us to an earlier era of pattern recognition and extrapolation, this time aided by computational power. Another approach could lead us to insights that continue to be expressed in mathematical equations. In either approach, or any synthesis of those, it is clearly no longer the steady march of the last few decades, continuing to add detail to ever more elaborate models. In this prospectus, we attempt to show the outlines how this may unfold in the coming decades, a new harnessing of physical knowledge, computation, and data.