Learning Causal Response Representations through Direct Effect Analysis
Paper and Code
Mar 06, 2025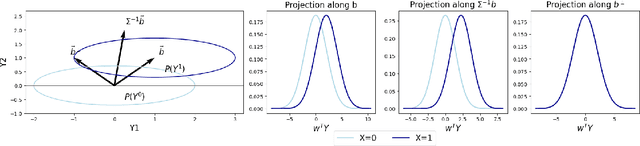

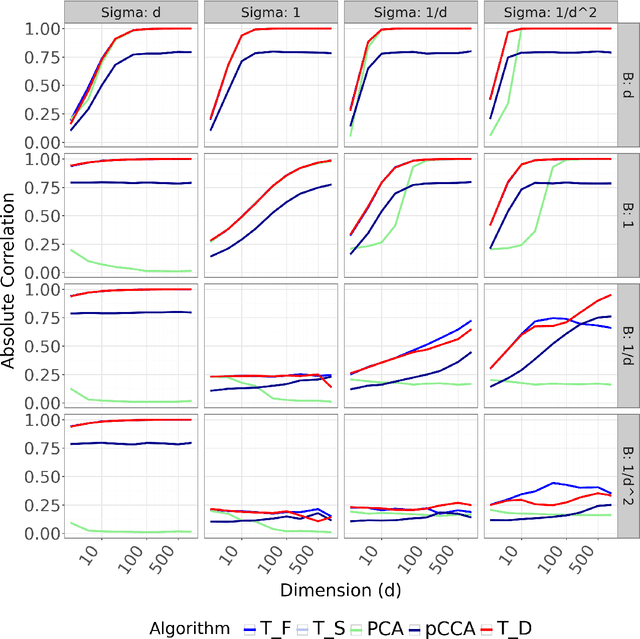

We propose a novel approach for learning causal response representations. Our method aims to extract directions in which a multidimensional outcome is most directly caused by a treatment variable. By bridging conditional independence testing with causal representation learning, we formulate an optimisation problem that maximises the evidence against conditional independence between the treatment and outcome, given a conditioning set. This formulation employs flexible regression models tailored to specific applications, creating a versatile framework. The problem is addressed through a generalised eigenvalue decomposition. We show that, under mild assumptions, the distribution of the largest eigenvalue can be bounded by a known $F$-distribution, enabling testable conditional independence. We also provide theoretical guarantees for the optimality of the learned representation in terms of signal-to-noise ratio and Fisher information maximisation. Finally, we demonstrate the empirical effectiveness of our approach in simulation and real-world experiments. Our results underscore the utility of this framework in uncovering direct causal effects within complex, multivariate settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge