Emily King
The Flag Median and FlagIRLS
Mar 08, 2022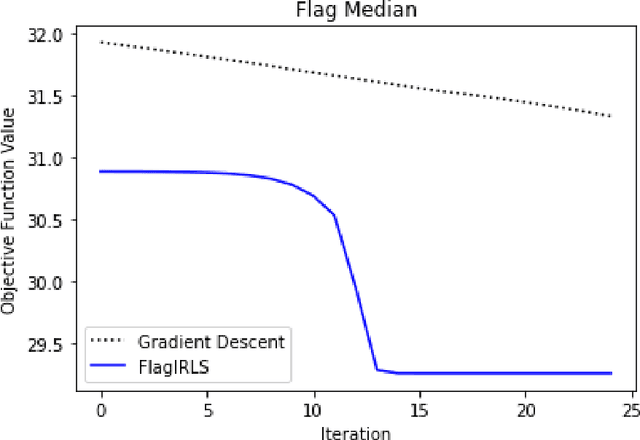
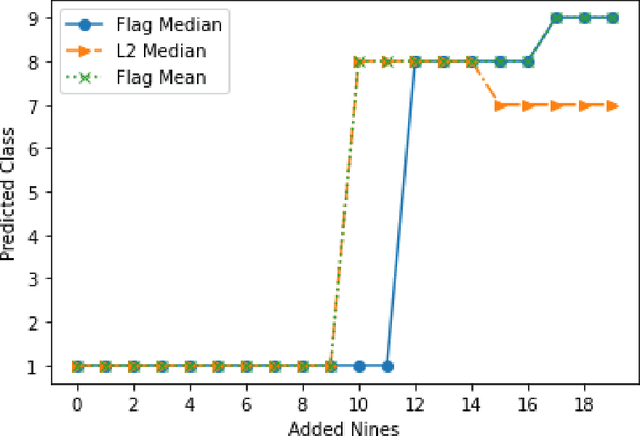
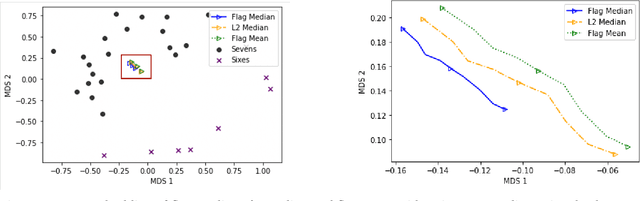
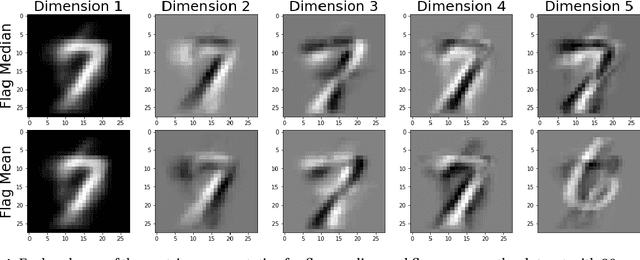
Abstract:Finding prototypes (e.g., mean and median) for a dataset is central to a number of common machine learning algorithms. Subspaces have been shown to provide useful, robust representations for datasets of images, videos and more. Since subspaces correspond to points on a Grassmann manifold, one is led to consider the idea of a subspace prototype for a Grassmann-valued dataset. While a number of different subspace prototypes have been described, the calculation of some of these prototypes has proven to be computationally expensive while other prototypes are affected by outliers and produce highly imperfect clustering on noisy data. This work proposes a new subspace prototype, the flag median, and introduces the FlagIRLS algorithm for its calculation. We provide evidence that the flag median is robust to outliers and can be used effectively in algorithms like Linde-Buzo-Grey (LBG) to produce improved clusterings on Grassmannians. Numerical experiments include a synthetic dataset, the MNIST handwritten digits dataset, the Mind's Eye video dataset and the UCF YouTube action dataset. The flag median is compared the other leading algorithms for computing prototypes on the Grassmannian, namely, the $\ell_2$-median and to the flag mean. We find that using FlagIRLS to compute the flag median converges in $4$ iterations on a synthetic dataset. We also see that Grassmannian LBG with a codebook size of $20$ and using the flag median produces at least a $10\%$ improvement in cluster purity over Grassmannian LBG using the flag mean or $\ell_2$-median on the Mind's Eye dataset.
Nonclosedness of the Set of Neural Networks in Sobolev Space
Jul 23, 2020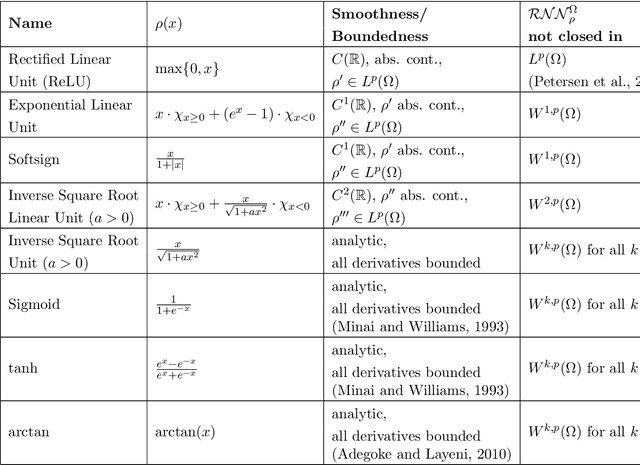
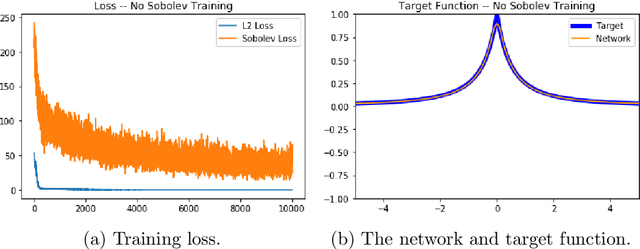
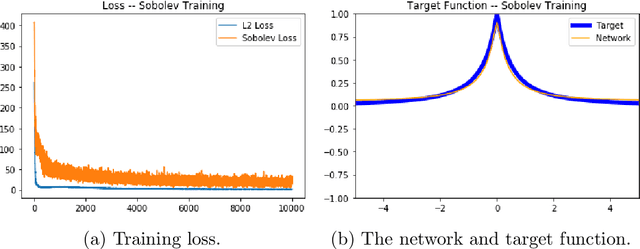
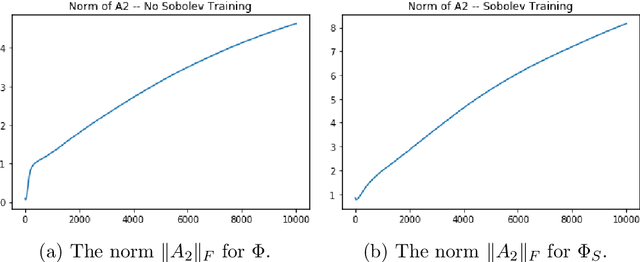
Abstract:We examine the closedness of the set of realized neural networks of a fixed architecture in Sobolev space. For an exactly $m$-times differentiable activation function $\rho$, we construct a sequence of neural networks $(\Phi_n)_{n \in \mathbb{N}}$ whose realizations converge in order-$(m-1)$ Sobolev norm to a function that cannot be realized exactly by a neural network. Thus, the set of realized neural networks is not closed in the order-$(m-1)$ Sobolev space $W^{m-1,p}$. We further show that this set is not closed in $W^{m,p}$ under slightly stronger conditions on the $m$-th derivative of $\rho$. For a real analytic activation function, we show that the set of realized neural networks is not closed in $W^{k,p}$ for any $k \in \mathbb{N}$. These results suggest that training a network to approximate a target function in Sobolev norm does not prevent parameter explosion. Finally, we present experimental results demonstrating that parameter explosion occurs in stochastic training regardless of the norm under which the network is trained. However, the network is still capable of closely approximating a non-network target function with network parameters that grow at a manageable rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge