Nonclosedness of the Set of Neural Networks in Sobolev Space
Paper and Code
Jul 23, 2020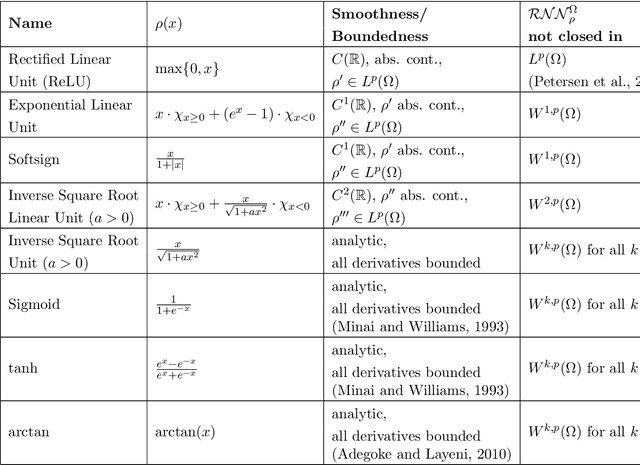
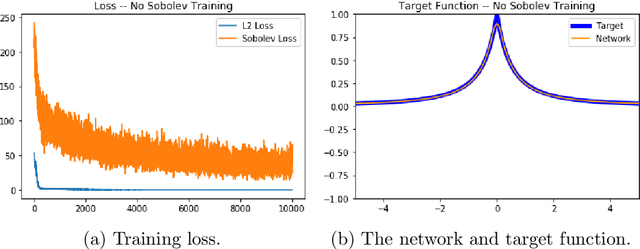
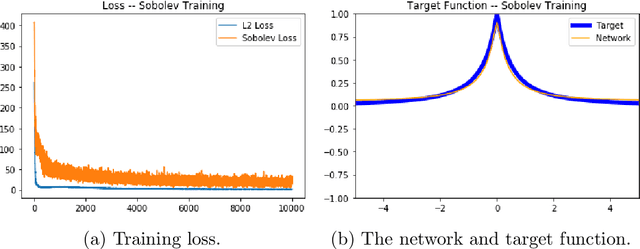
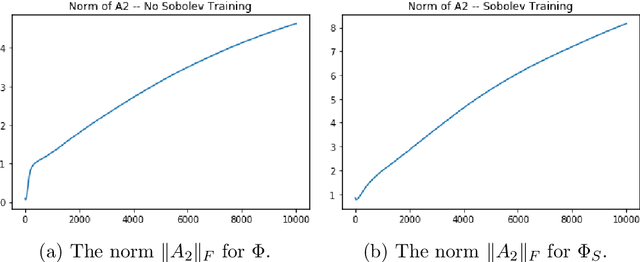
We examine the closedness of the set of realized neural networks of a fixed architecture in Sobolev space. For an exactly $m$-times differentiable activation function $\rho$, we construct a sequence of neural networks $(\Phi_n)_{n \in \mathbb{N}}$ whose realizations converge in order-$(m-1)$ Sobolev norm to a function that cannot be realized exactly by a neural network. Thus, the set of realized neural networks is not closed in the order-$(m-1)$ Sobolev space $W^{m-1,p}$. We further show that this set is not closed in $W^{m,p}$ under slightly stronger conditions on the $m$-th derivative of $\rho$. For a real analytic activation function, we show that the set of realized neural networks is not closed in $W^{k,p}$ for any $k \in \mathbb{N}$. These results suggest that training a network to approximate a target function in Sobolev norm does not prevent parameter explosion. Finally, we present experimental results demonstrating that parameter explosion occurs in stochastic training regardless of the norm under which the network is trained. However, the network is still capable of closely approximating a non-network target function with network parameters that grow at a manageable rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge