ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

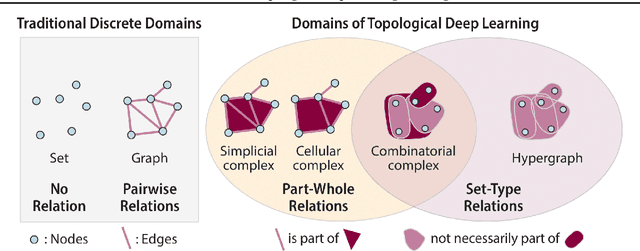
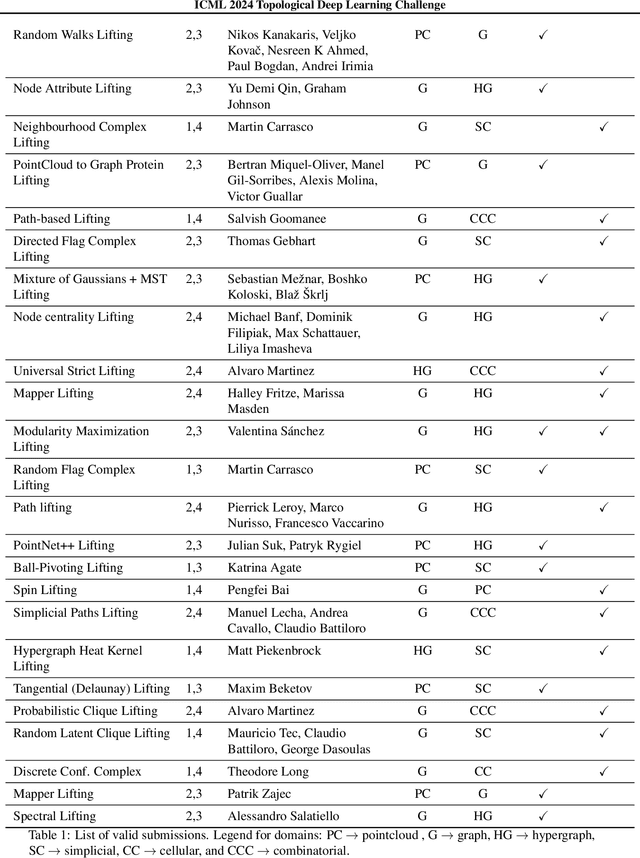
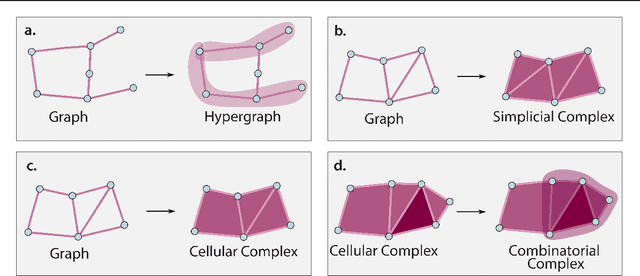
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

Point Cloud Classification via Deep Set Linearized Optimal Transport

We introduce Deep Set Linearized Optimal Transport, an algorithm designed for the efficient simultaneous embedding of point clouds into an $L^2-$space. This embedding preserves specific low-dimensional structures within the Wasserstein space while constructing a classifier to distinguish between various classes of point clouds. Our approach is motivated by the observation that $L^2-$distances between optimal transport maps for distinct point clouds, originating from a shared fixed reference distribution, provide an approximation of the Wasserstein-2 distance between these point clouds, under certain assumptions. To learn approximations of these transport maps, we employ input convex neural networks (ICNNs) and establish that, under specific conditions, Euclidean distances between samples from these ICNNs closely mirror Wasserstein-2 distances between the true distributions. Additionally, we train a discriminator network that attaches weights these samples and creates a permutation invariant classifier to differentiate between different classes of point clouds. We showcase the advantages of our algorithm over the standard deep set approach through experiments on a flow cytometry dataset with a limited number of labeled point clouds.

Semi-Supervised Manifold Learning with Complexity Decoupled Chart Autoencoders

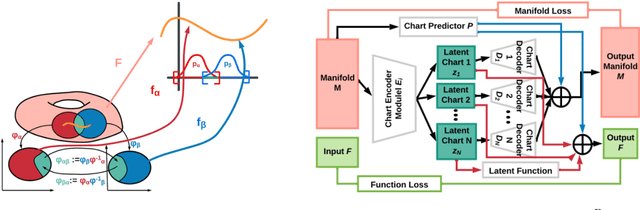
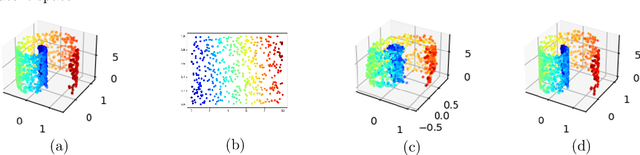
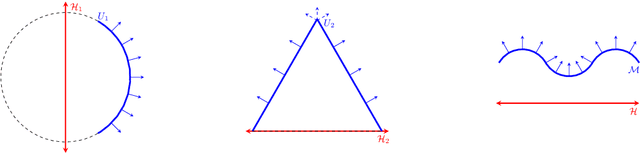
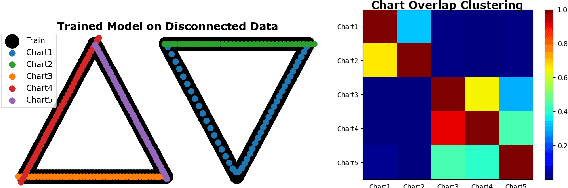
Autoencoding is a popular method in representation learning. Conventional autoencoders employ symmetric encoding-decoding procedures and a simple Euclidean latent space to detect hidden low-dimensional structures in an unsupervised way. This work introduces a chart autoencoder with an asymmetric encoding-decoding process that can incorporate additional semi-supervised information such as class labels. Besides enhancing the capability for handling data with complicated topological and geometric structures, these models can successfully differentiate nearby but disjoint manifolds and intersecting manifolds with only a small amount of supervision. Moreover, this model only requires a low complexity encoder, such as local linear projection. We discuss the theoretical approximation power of such networks that essentially depends on the intrinsic dimension of the data manifold and not the dimension of the observations. Our numerical experiments on synthetic and real-world data verify that the proposed model can effectively manage data with multi-class nearby but disjoint manifolds of different classes, overlapping manifolds, and manifolds with non-trivial topology.

DNA: Dynamic Network Augmentation

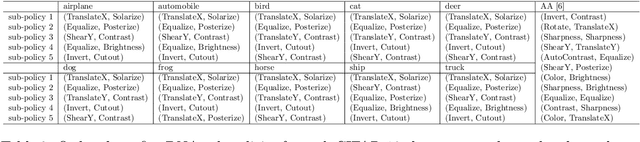
In many classification problems, we want a classifier that is robust to a range of non-semantic transformations. For example, a human can identify a dog in a picture regardless of the orientation and pose in which it appears. There is substantial evidence that this kind of invariance can significantly improve the accuracy and generalization of machine learning models. A common technique to teach a model geometric invariances is to augment training data with transformed inputs. However, which invariances are desired for a given classification task is not always known. Determining an effective data augmentation policy can require domain expertise or extensive data pre-processing. Recent efforts like AutoAugment optimize over a parameterized search space of data augmentation policies to automate the augmentation process. While AutoAugment and similar methods achieve state-of-the-art classification accuracy on several common datasets, they are limited to learning one data augmentation policy. Often times different classes or features call for different geometric invariances. We introduce Dynamic Network Augmentation (DNA), which learns input-conditional augmentation policies. Augmentation parameters in our model are outputs of a neural network and are implicitly learned as the network weights are updated. Our model allows for dynamic augmentation policies and performs well on data with geometric transformations conditional on input features.

Rotating spiders and reflecting dogs: a class conditional approach to learning data augmentation distributions

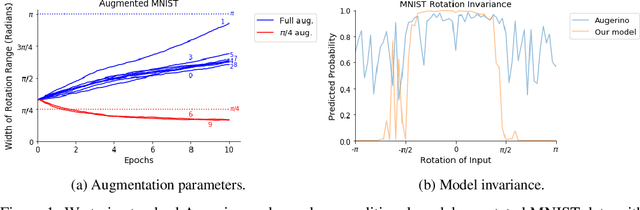
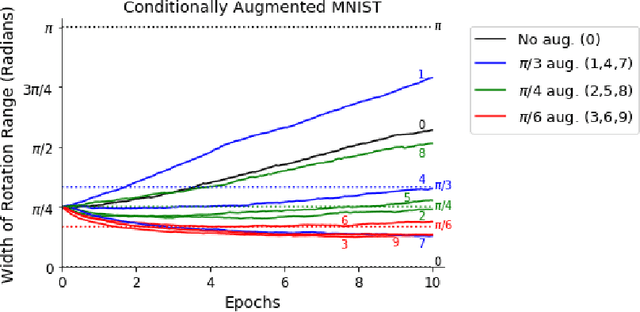
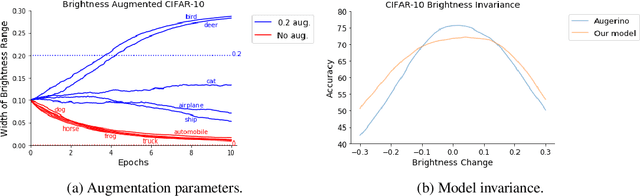
Building invariance to non-meaningful transformations is essential to building efficient and generalizable machine learning models. In practice, the most common way to learn invariance is through data augmentation. There has been recent interest in the development of methods that learn distributions on augmentation transformations from the training data itself. While such approaches are beneficial since they are responsive to the data, they ignore the fact that in many situations the range of transformations to which a model needs to be invariant changes depending on the particular class input belongs to. For example, if a model needs to be able to predict whether an image contains a starfish or a dog, we may want to apply random rotations to starfish images during training (since these do not have a preferred orientation), but we would not want to do this to images of dogs. In this work we introduce a method by which we can learn class conditional distributions on augmentation transformations. We give a number of examples where our methods learn different non-meaningful transformations depending on class and further show how our method can be used as a tool to probe the symmetries intrinsic to a potentially complex dataset.

Nonclosedness of the Set of Neural Networks in Sobolev Space

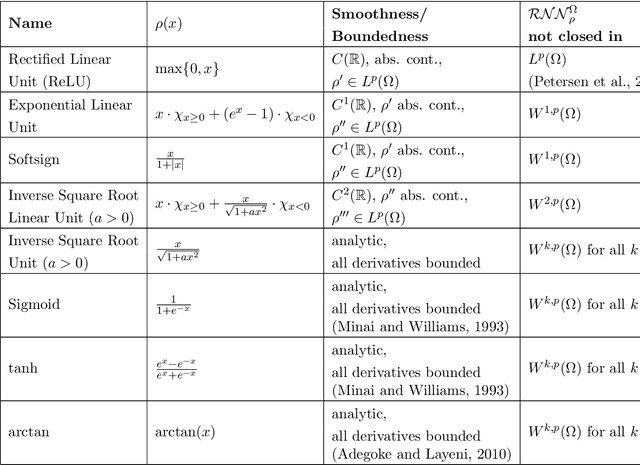
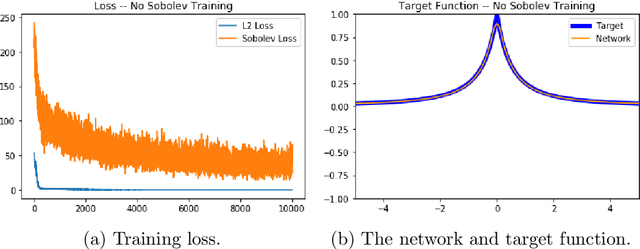
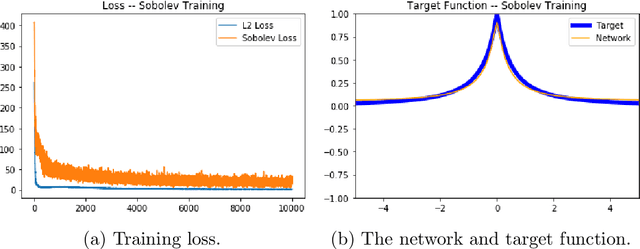
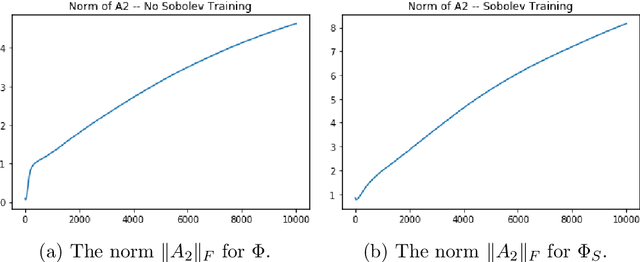
We examine the closedness of the set of realized neural networks of a fixed architecture in Sobolev space. For an exactly $m$-times differentiable activation function $\rho$, we construct a sequence of neural networks $(\Phi_n)_{n \in \mathbb{N}}$ whose realizations converge in order-$(m-1)$ Sobolev norm to a function that cannot be realized exactly by a neural network. Thus, the set of realized neural networks is not closed in the order-$(m-1)$ Sobolev space $W^{m-1,p}$. We further show that this set is not closed in $W^{m,p}$ under slightly stronger conditions on the $m$-th derivative of $\rho$. For a real analytic activation function, we show that the set of realized neural networks is not closed in $W^{k,p}$ for any $k \in \mathbb{N}$. These results suggest that training a network to approximate a target function in Sobolev norm does not prevent parameter explosion. Finally, we present experimental results demonstrating that parameter explosion occurs in stochastic training regardless of the norm under which the network is trained. However, the network is still capable of closely approximating a non-network target function with network parameters that grow at a manageable rate.