ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

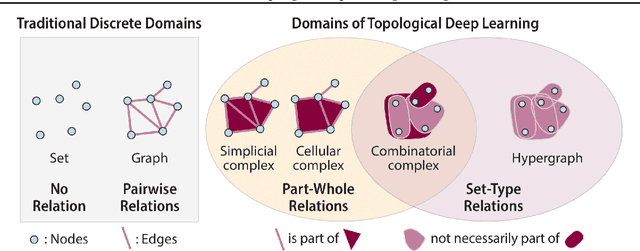
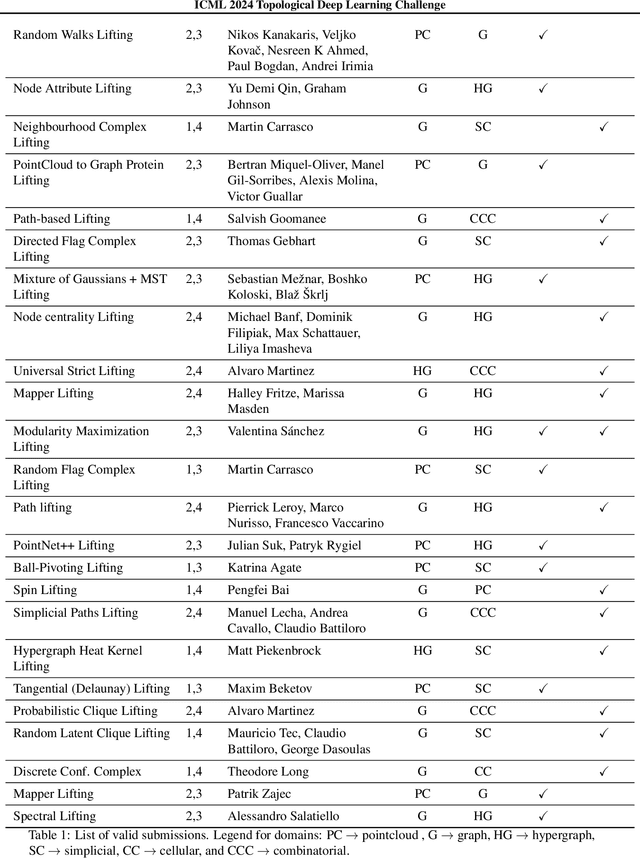
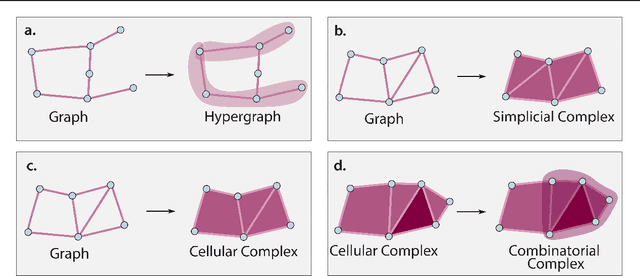
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

ICML 2023 Topological Deep Learning Challenge : Design and Results

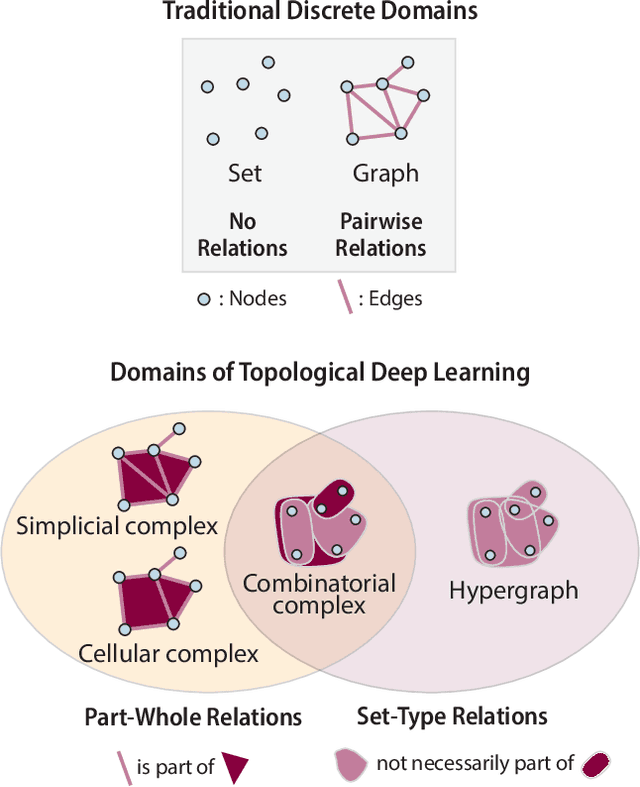
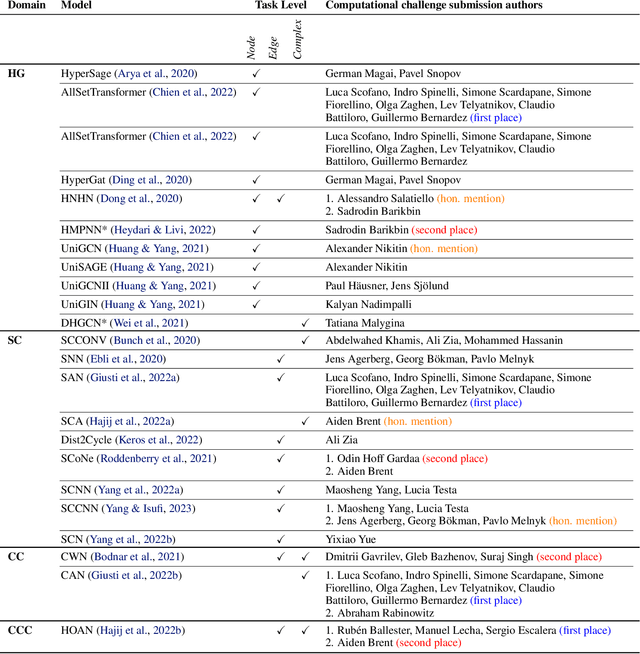
This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.

How many dimensions are required to find an adversarial example?

Past work exploring adversarial vulnerability have focused on situations where an adversary can perturb all dimensions of model input. On the other hand, a range of recent works consider the case where either (i) an adversary can perturb a limited number of input parameters or (ii) a subset of modalities in a multimodal problem. In both of these cases, adversarial examples are effectively constrained to a subspace $V$ in the ambient input space $\mathcal{X}$. Motivated by this, in this work we investigate how adversarial vulnerability depends on $\dim(V)$. In particular, we show that the adversarial success of standard PGD attacks with $\ell^p$ norm constraints behaves like a monotonically increasing function of $\epsilon (\frac{\dim(V)}{\dim \mathcal{X}})^{\frac{1}{q}}$ where $\epsilon$ is the perturbation budget and $\frac{1}{p} + \frac{1}{q} =1$, provided $p > 1$ (the case $p=1$ presents additional subtleties which we analyze in some detail). This functional form can be easily derived from a simple toy linear model, and as such our results land further credence to arguments that adversarial examples are endemic to locally linear models on high dimensional spaces.

DNA: Dynamic Network Augmentation

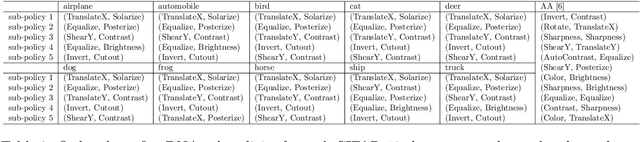
In many classification problems, we want a classifier that is robust to a range of non-semantic transformations. For example, a human can identify a dog in a picture regardless of the orientation and pose in which it appears. There is substantial evidence that this kind of invariance can significantly improve the accuracy and generalization of machine learning models. A common technique to teach a model geometric invariances is to augment training data with transformed inputs. However, which invariances are desired for a given classification task is not always known. Determining an effective data augmentation policy can require domain expertise or extensive data pre-processing. Recent efforts like AutoAugment optimize over a parameterized search space of data augmentation policies to automate the augmentation process. While AutoAugment and similar methods achieve state-of-the-art classification accuracy on several common datasets, they are limited to learning one data augmentation policy. Often times different classes or features call for different geometric invariances. We introduce Dynamic Network Augmentation (DNA), which learns input-conditional augmentation policies. Augmentation parameters in our model are outputs of a neural network and are implicitly learned as the network weights are updated. Our model allows for dynamic augmentation policies and performs well on data with geometric transformations conditional on input features.

Rotating spiders and reflecting dogs: a class conditional approach to learning data augmentation distributions

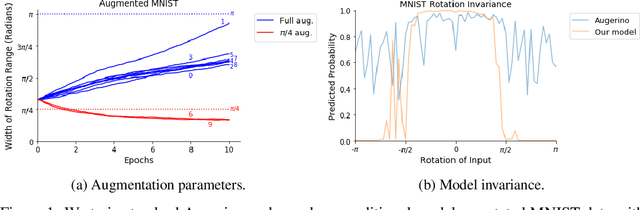
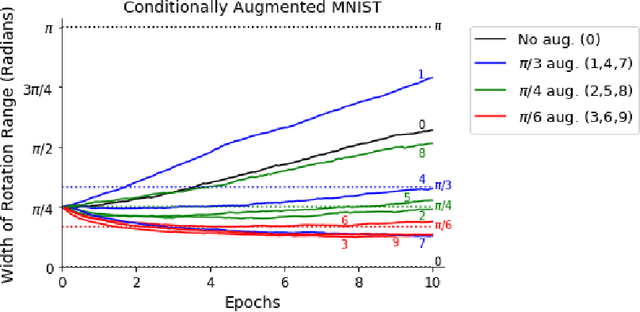
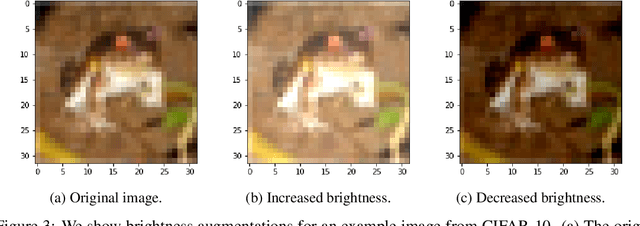
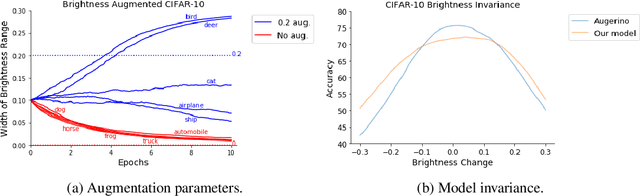
Building invariance to non-meaningful transformations is essential to building efficient and generalizable machine learning models. In practice, the most common way to learn invariance is through data augmentation. There has been recent interest in the development of methods that learn distributions on augmentation transformations from the training data itself. While such approaches are beneficial since they are responsive to the data, they ignore the fact that in many situations the range of transformations to which a model needs to be invariant changes depending on the particular class input belongs to. For example, if a model needs to be able to predict whether an image contains a starfish or a dog, we may want to apply random rotations to starfish images during training (since these do not have a preferred orientation), but we would not want to do this to images of dogs. In this work we introduce a method by which we can learn class conditional distributions on augmentation transformations. We give a number of examples where our methods learn different non-meaningful transformations depending on class and further show how our method can be used as a tool to probe the symmetries intrinsic to a potentially complex dataset.